Алгоритм Борувки — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
м (→‎Описание алгоритма)
(→‎Доказательство корректности)
Строка 13: Строка 13:
  
 
==Доказательство корректности==
 
==Доказательство корректности==
−
{{Лемма
 
−
|id=lemma1
 
−
|statement=Рассмотрим связный неориентированный взвешенный граф <tex> G = (V, E)  </tex> с инъективной весовой функцией <tex>w : E \to \mathbb{R}</tex> .
 
−
Тогда после первой итерации главного цикла алгоритма Борувки получившийся подграф можно достроить до ''MST''.
 
−
|proof=Предположим обратное: пусть любое ''MST'' графа <tex>G</tex> не содержит <tex>T</tex>. Рассмотрим какое-нибудь ''MST''. Тогда существует ребро <tex>x</tex> из <tex>T</tex> такое что <tex>x</tex> не принадлежит ''MST''. Добавив ребро <tex>x</tex> в ''MST'', получаем цикл в котором <tex>x</tex> не максимально, т.к оно было минимальным. Тогда, исходя из [[Критерий Тарьяна минимальности остовного дерева|критерия Тарьяна]], получаем противоречие.
 
−
}}
 
−
 
  
 
{{Теорема
 
{{Теорема
−
|id=th1.
+
|statement= Алгоритм Борувки строит '''MST'''
−
|statement=Алгоритм Борувки строит ''MST''.
+
|proof=Очевидно, что в результате работы алгоритма получается дерево. Пусть <tex> T </tex> {{---}} минимальное остовное дерево графа <tex> G </tex>, а <tex> T' </tex> {{---}} дерево полученное после работы алгоритма.
−
|proof=Очевидно, что алгоритм Борувки строит дерево.Будем доказывать что после каждой итерации главного цикла в алгоритме Борувки текущий подграф <tex>T</tex> можно достроить до ''MST''. Докажем это по индукции.
 
  
−
'''База. '''  <tex>n = 1</tex> (см. [[#lemma1|Лемму]]).
+
Покажем, что <tex> T = T'</tex>.  
  
−
'''Переход. '''  Пусть лес <tex>T</tex>, получившийся после <tex>n</tex> итераций алгоритма, можно достроить до ''MST''. Докажем, что после <tex>n+1</tex> итерации получившийся лес <tex>T'</tex> можно достроить до ''MST''. Предположим обратное: <tex>T'</tex> нельзя достроить до ''MST''. Тогда существует <tex>F</tex> = ''MST'' графа <tex>G</tex>, содержащее <tex>T</tex>  и не содержащее <tex>T'</tex>. Тогда рассмотрим цикл, получающийся добавлением в <tex>F</tex> какого-нибудь ребра <tex>x</tex> из <tex>T' {{---}} T</tex>. На этом цикле имеется ребро, большее по весу чем ребро <tex>x</tex>, иначе компонента для которой <tex>x</tex> является минимальным ребром ни с кем больше ни связана. Исходя из  [[Критерий Тарьяна минимальности остовного дерева|критерия Тарьяна]], получаем противоречие.
+
Предположим обратное <tex> T \neq T' </tex>. Пусть ребро <tex> e' </tex> {{---}} первое окрашенное ребро дерева <tex> T' </tex>, не принадлежащее дереву <tex> T </tex>. Пусть <tex> P </tex> {{---}} путь, соединяющий в дереве <tex> T </tex> вершины ребра <tex> e' </tex>.  
  
−
'''Получаем. '''  <tex>T'</tex> можно достроить до ''MST''. Следовательно предположение индукции верно.
+
Понятно, что в момент, когда ребро <tex> e' </tex> красили, какое-то ребро <tex> P </tex> (назовем его <tex> e </tex>) не было покрашено. По алгоритму <tex> w(e) > w(e') </tex>. Однако тогда <tex> T - e + e' </tex> {{---}} остовное дерево меньшего веса. Получили противоречение. Следовательно <tex> T = T'</tex>.
−
 
 
}}
 
}}
  

Версия 00:26, 11 октября 2015

Алгоритм Борувки (англ. Borůvka's algorithm) — алгоритм поиска минимального остовного дерева (англ. minimum spanning tree, MST) во взвешенном неориентированном связном графе. Впервые был опубликован в 1926 году Отакаром Борувкой.

Описание алгоритма

  1. Построим граф [math]T[/math]. Изначально [math]T[/math] содержит все вершины из [math]G[/math] и не содержит ребер (каждая вершина в графе [math]T[/math] — отдельная компонента связности).
  2. Для каждой компоненты связности находим минимальное по весу ребро, которое связывает эту компоненту с другой.
  3. Добавим в [math]T[/math] все найденные рёбра.
  4. Повторяем пункты [math] 2 [/math] и [math] 3 [/math], пока граф [math] T [/math] не станет деревом.

Данный алгоритм может работать неправильно, если в графе есть ребра равные по весу. Например, полный граф из трех вершин, вес каждого ребра равен один. В [math]T[/math] могут быть добавлены все три ребра. Избежать эту проблему можно, выбирая в первом пункте среди ребер, равных по весу, ребро с наименьшим номером.

Доказательство будем проводить, считая веса всех ребер различными.

Доказательство корректности

Теорема:
Алгоритм Борувки строит MST
Доказательство:
[math]\triangleright[/math]

Очевидно, что в результате работы алгоритма получается дерево. Пусть [math] T [/math] — минимальное остовное дерево графа [math] G [/math], а [math] T' [/math] — дерево полученное после работы алгоритма.

Покажем, что [math] T = T'[/math].

Предположим обратное [math] T \neq T' [/math]. Пусть ребро [math] e' [/math] — первое окрашенное ребро дерева [math] T' [/math], не принадлежащее дереву [math] T [/math]. Пусть [math] P [/math] — путь, соединяющий в дереве [math] T [/math] вершины ребра [math] e' [/math].

Понятно, что в момент, когда ребро [math] e' [/math] красили, какое-то ребро [math] P [/math] (назовем его [math] e [/math]) не было покрашено. По алгоритму [math] w(e) \gt w(e') [/math]. Однако тогда [math] T - e + e' [/math] — остовное дерево меньшего веса. Получили противоречение. Следовательно [math] T = T'[/math].
[math]\triangleleft[/math]

Реализация

У вершины есть поле comp — компонента связности, которой принадлежит эта вершина. 

  // [math]G[/math] — исходный граф
  // [math]w[/math] — весовая функция
  function [math]\mathtt{boruvkaMST}():[/math]
      while [math]T\mathtt{.size} \lt  n - 1[/math]                                   
           for [math]k \in [/math] Component                                 // Component — множество компонент связности в [math]T[/math]
               [math]w(\mathtt{minEdge}[k])=\infty[/math]                      // для каждой компоненты связности вес минимального ребра = [math]\infty[/math]
           [math]\mathtt{findComp(}T\mathtt{)}[/math]                                      // разбиваем граф [math]T[/math] на компоненты связности обычным dfs-ом
           for [math]\mathtt{(u,v)} \in  E [/math]
               if [math]\mathtt{u.comp} \neq \mathtt{v.comp}[/math]
                   if [math]w(\mathtt{minEdge}[\mathtt{u.comp}]) \lt  w(u,v)[/math]
                       [math]\mathtt{minEdge}[\mathtt{u.comp}] = (u,v)[/math]
                   if [math]w(\mathtt{minEdge}[\mathtt{v.comp}]) \lt  w(u,v)[/math]
                       [math]\mathtt{minEdge}[\mathtt{v.comp}] = (u,v)[/math]
           for [math]k \in [/math] Component                                 
               [math]T\mathtt{.addEdge}(\mathtt{minEdge}[k])[/math]                     // добавляем ребро если его не было в [math]T[/math]
      return [math]T[/math]

Пример

Изображение Компоненты связности Описание
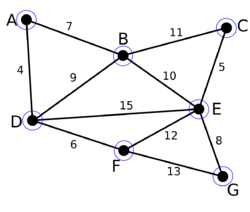
Boruvka 1.png {A}
{B}
{C}
{D}
{E}
{F}
{G} 		Начальный граф [math]G[/math]. Каждая вершина является компонентой (синие окружности).
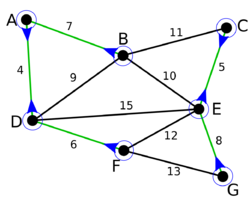
Boruvka 2.png {ABDF}
{CEG} 		На первой итерации внешнего цикла для каждой компоненты были добавлены минимальные сопряженные ребра. Некоторые ребра добавлены несколько раз ([math]AD[/math] и [math]CE[/math]). Осталось две компоненты.
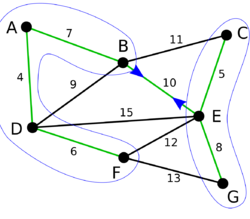
Boruvka 3.png {ABCDEFG} На последней итерации внешнего цикла было добавлено минимальное ребро, соединяющее две оставшиеся компоненты (ребро [math]BE[/math]). Осталась одна компонента. Минимальное остовное дерево графа [math]G[/math] построено.

Асимптотика

Внешний цикл повторяется [math]\log{V}[/math] раз, так как количество компонент связности каждый раз уменьшается в двое и изначально равно количеству вершин. Что же касается внутреннего цикла, то он выполняется за [math]E[/math], где [math]E[/math] — количество рёбер в исходном графе. Следовательно конечное время работы алгоритма [math]O(E\log{V})[/math].

См. также

Источники информации

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Алгоритм_Борувки&oldid=49612»