Алгоритм Борувки — различия между версиями
Novik (обсуждение | вклад) (→Описание алгоритма) |
Novik (обсуждение | вклад) м (→Описание алгоритма) |
||
| Строка 3: | Строка 3: | ||
==Описание алгоритма== | ==Описание алгоритма== | ||
| − | # Изначально все ребра | + | # Изначально все ребра <tex>G</tex> не окрашены, а каждая вершина графа {{---}} тривиальное дерево. |
# Для каждого дерева <tex> T </tex> найдем минимальное инцидентное ему ребро. Окрасим все такие ребра. | # Для каждого дерева <tex> T </tex> найдем минимальное инцидентное ему ребро. Окрасим все такие ребра. | ||
# Повторяем шаг <tex> 2 </tex> пока в графе не останется только одно дерево <tex> T </tex>. | # Повторяем шаг <tex> 2 </tex> пока в графе не останется только одно дерево <tex> T </tex>. | ||
Версия 00:42, 11 октября 2015
Алгоритм Борувки (англ. Borůvka's algorithm) — алгоритм поиска минимального остовного дерева (англ. minimum spanning tree, MST) во взвешенном неориентированном связном графе. Впервые был опубликован в 1926 году Отакаром Борувкой.
Содержание
Описание алгоритма
- Изначально все ребра не окрашены, а каждая вершина графа — тривиальное дерево.
- Для каждого дерева найдем минимальное инцидентное ему ребро. Окрасим все такие ребра.
- Повторяем шаг пока в графе не останется только одно дерево .
Данный алгоритм может работать неправильно, если в графе есть ребра равные по весу. Например, полный граф из трех вершин, вес каждого ребра равен один. В могут быть добавлены все три ребра. Избежать эту проблему можно, выбирая в первом пункте среди ребер, равных по весу, ребро с наименьшим номером.
Доказательство корректности
| Теорема: |
Алгоритм Борувки строит MST |
| Доказательство: |
|
Очевидно, что в результате работы алгоритма получается дерево. Пусть — минимальное остовное дерево графа , а — дерево полученное после работы алгоритма. Покажем, что . Предположим обратное . Пусть ребро — первое окрашенное ребро дерева , не принадлежащее дереву . Пусть — путь, соединяющий в дереве вершины ребра . Понятно, что в момент, когда ребро красили, какое-то ребро (назовем его ) не было покрашено. По алгоритму . Однако тогда — остовное дерево меньшего веса. Получили противоречение. Следовательно . |
Реализация
У вершины есть поле comp — компонента связности, которой принадлежит эта вершина.
// — исходный граф // — весовая функция function while for Component // Component — множество компонент связности в // для каждой компоненты связности вес минимального ребра = // разбиваем граф на компоненты связности обычным dfs-ом for if if if for Component // добавляем ребро если его не было в return |
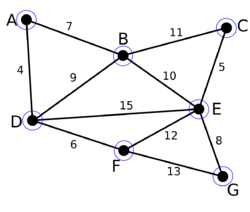
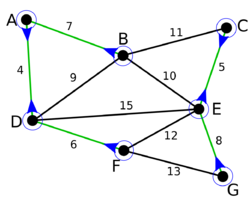
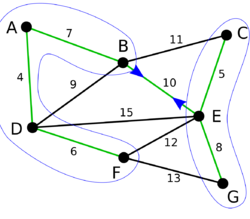
Пример
Асимптотика
Внешний цикл повторяется раз, так как количество компонент связности каждый раз уменьшается в двое и изначально равно количеству вершин. Что же касается внутреннего цикла, то он выполняется за , где — количество рёбер в исходном графе. Следовательно конечное время работы алгоритма .