Представление целых чисел: прямой код, код со сдвигом, дополнительный код — различия между версиями
(→Дополнительный код (дополнение до двух)) |
(Выполнен тикет 4.2 (пункт 7 выполнен частично)) |
||
| Строка 9: | Строка 9: | ||
== Прямой код == | == Прямой код == | ||
[[Файл:Представление двоичных чисел в прямом коде.jpg|230px|thumb|right|Нумерация двоичных чисел в прямом представлении]] | [[Файл:Представление двоичных чисел в прямом коде.jpg|230px|thumb|right|Нумерация двоичных чисел в прямом представлении]] | ||
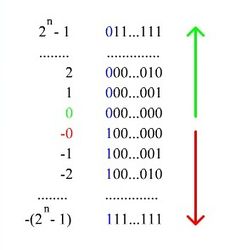
| − | При записи числа в '''прямом коде''' (англ. '' | + | При записи числа в '''прямом коде''' (англ. ''Signed magnitude representation'') старший разряд является знаковым разрядом. Если его значение равно нулю, то представлено положительное число или положительный ноль, если единице, то представлено отрицательное число или отрицательный ноль. В остальных разрядах (которые называются цифровыми) записывается двоичное представление модуля числа. Например, число <tex> -5 </tex> в восьмибитном типе данных, использующем прямой код, будет выглядеть так: <tex> 10000101 </tex>. |
Таким способом в <tex> n </tex>-битовом типе данных можно представить диапазон чисел <tex> [-2^{n-1} + 1; 2^{n-1} - 1] </tex>. | Таким способом в <tex> n </tex>-битовом типе данных можно представить диапазон чисел <tex> [-2^{n-1} + 1; 2^{n-1} - 1] </tex>. | ||
| − | + | === Достоинства представления чисел с помощью прямого кода === | |
*получить прямой код числа достаточно просто. | *получить прямой код числа достаточно просто. | ||
| − | + | === Недостатки представления чисел с помощью прямого кода === | |
*выполнение арифметических операций с отрицательными числами требует усложнения архитектуры центрального процессора (например, для вычитания невозможно использовать сумматор, необходима отдельная схема для этого); | *выполнение арифметических операций с отрицательными числами требует усложнения архитектуры центрального процессора (например, для вычитания невозможно использовать сумматор, необходима отдельная схема для этого); | ||
| − | *существуют два нуля <tex> +0 </tex> и <tex> -0 </tex>, из-за чего усложняется арифметическое сравнение. | + | *существуют два нуля: <tex> +0 </tex> <tex>(100 \ldots 000) </tex> и <tex> -0 </tex> <tex> (000 \ldots 000) </tex>, из-за чего усложняется арифметическое сравнение. |
| − | Из-за | + | Из-за весьма существенных недостатков прямой код используется очень редко. |
== Код со сдвигом == | == Код со сдвигом == | ||
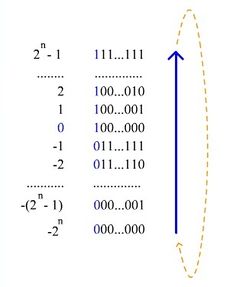
| − | [[Файл:Представление двоичных чисел в коде со сдвигом.jpg|230px|thumb|right|Код со сдвигом. Как видно, двоичное представление зациклено по модулю <tex | + | [[Файл:Представление двоичных чисел в коде со сдвигом.jpg|230px|thumb|right|Код со сдвигом. Как видно, двоичное представление зациклено по модулю <tex>1000..000_{(2)}</tex> (<tex>n</tex> нулей)]] |
| − | При использовании '''кода со сдвигом''' ('' | + | При использовании '''кода со сдвигом''' (англ. ''Offset binary'') целочисленный отрезок от нуля до <tex> 2^n </tex> (<tex> n </tex> — количество бит) сдвигается влево на <tex> 2^{n-1} </tex>, а затем получившиеся на этом отрезке числа последовательно кодируются в порядке возрастания кодами от <tex> 000 \dots 0 </tex> до <tex> 111 \dots 1 </tex>. Например, число <tex> -5 </tex> в восьмибитном типе данных, использующем код со сдвигом, превратится в <tex> -5 + 128 = 123 </tex>, то есть будет выглядеть так: <tex> 01111011 </tex>. |
По сути, при таком кодировании: | По сути, при таком кодировании: | ||
| Строка 35: | Строка 35: | ||
Можно получить диапазон значений <tex> [-2^{n-1}; 2^{n-1} - 1]</tex>. | Можно получить диапазон значений <tex> [-2^{n-1}; 2^{n-1} - 1]</tex>. | ||
| − | + | === Достоинства представления чисел с помощью кода со сдвигом === | |
*не требуется усложнение архитектуры процессора; | *не требуется усложнение архитектуры процессора; | ||
*нет проблемы двух нулей. | *нет проблемы двух нулей. | ||
| − | + | === Недостатки представления чисел с помощью кода со сдвигом === | |
*при арифметических операциях нужно учитывать смещение, то есть проделывать на одно действие больше (например, после «обычного» сложения двух чисел у результата будет двойное смещение, одно из которых необходимо вычесть); | *при арифметических операциях нужно учитывать смещение, то есть проделывать на одно действие больше (например, после «обычного» сложения двух чисел у результата будет двойное смещение, одно из которых необходимо вычесть); | ||
| − | *ряд положительных и отрицательных чисел несимметричен. | + | *ряд положительных и отрицательных чисел несимметричен. |
Из-за необходимости усложнять арифметические операции код со сдвигом для представления целых чисел используется не часто, но зато применяется для хранения порядка [[Представление вещественных чисел|вещественного числа]]. | Из-за необходимости усложнять арифметические операции код со сдвигом для представления целых чисел используется не часто, но зато применяется для хранения порядка [[Представление вещественных чисел|вещественного числа]]. | ||
| Строка 49: | Строка 49: | ||
== Дополнительный код (дополнение до единицы) == | == Дополнительный код (дополнение до единицы) == | ||
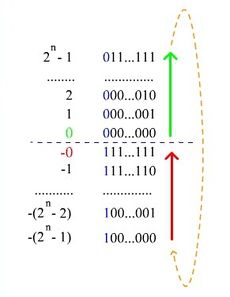
[[Файл:Представление_чисел_дополнением_до_единицы.jpg|230px|thumb|right|Нумерация двоичных чисел в представлении c дополнением до единицы. В отличии от кода со сдвигом, нулю соответствуют коды <tex> 00...000 </tex> и <tex> 11...111 </tex>]] | [[Файл:Представление_чисел_дополнением_до_единицы.jpg|230px|thumb|right|Нумерация двоичных чисел в представлении c дополнением до единицы. В отличии от кода со сдвигом, нулю соответствуют коды <tex> 00...000 </tex> и <tex> 11...111 </tex>]] | ||
| − | В качестве альтернативы представления целых чисел может использоваться код с дополнением до единицы (англ. ''Ones' complement''). | + | В качестве альтернативы представления целых чисел может использоваться код с '''дополнением до единицы''' (англ. ''Ones' complement''). |
Алгоритм получения кода числа: | Алгоритм получения кода числа: | ||
*если число положительное, то в старший разряд (который является знаковым) записывается ноль, а далее записывается само число; | *если число положительное, то в старший разряд (который является знаковым) записывается ноль, а далее записывается само число; | ||
| − | *если число отрицательное, то код получается инвертированием представления модуля числа (получается | + | *если число отрицательное, то код получается инвертированием представления модуля числа (получается обратный код); |
| + | *если число является нулем, от его можно представить двумя способами: <tex> +0 </tex> <tex>(000 \ldots 000) </tex> или <tex> -0 </tex> <tex> (111 \ldots 111) </tex>. | ||
| − | Пример: переведём число <tex> -13 </tex> в восьмибитный код | + | Пример: переведём число <tex> -13 </tex> в двоичный восьмибитный код. Прямой код модуля <tex> -13 </tex>: <tex> 00001101 </tex>, инвертируем и получаем <tex> 11110010 </tex>. |
Для получения из дополнительного кода самого числа достаточно инвертировать все разряды кода. | Для получения из дополнительного кода самого числа достаточно инвертировать все разряды кода. | ||
Таким способом можно получить диапазон значений <tex> [-2^{n-1}+1; 2^{n-1} - 1] </tex>. | Таким способом можно получить диапазон значений <tex> [-2^{n-1}+1; 2^{n-1} - 1] </tex>. | ||
| − | + | === Достоинства представления чисел с помощью кода с дополнением до единицы === | |
| − | *Простое получение кода отрицательных чисел | + | *Простое получение кода отрицательных чисел. |
| − | + | === Недостатки представления чисел с помощью кода с дополнением до единицы === | |
| − | *выполнение арифметических операций с отрицательными числами требует усложнения архитектуры центрального процессора | + | *выполнение арифметических операций с отрицательными числами требует усложнения архитектуры центрального процессора; |
| − | *существуют два нуля <tex> +0 </tex> и <tex> -0 </tex>. | + | *существуют два нуля: <tex> +0 </tex> и <tex> -0 </tex>. |
== Дополнительный код (дополнение до двух) == | == Дополнительный код (дополнение до двух) == | ||
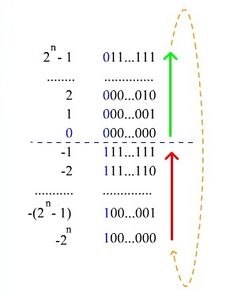
[[Файл:Представление двоичных чисел в дополнительном коде.jpg|230px|thumb|right|Нумерация двоичных чисел в представлении c дополнением до двух.]] | [[Файл:Представление двоичных чисел в дополнительном коде.jpg|230px|thumb|right|Нумерация двоичных чисел в представлении c дополнением до двух.]] | ||
| − | Чаще всего для представления отрицательных чисел используется код с дополнением до двух (англ. ''Two's complement''). | + | Чаще всего для представления отрицательных чисел используется код с '''дополнением до двух''' (англ. ''Two's complement''). |
Алгоритм получения дополнительного кода числа: | Алгоритм получения дополнительного кода числа: | ||
| Строка 80: | Строка 81: | ||
*если число отрицательное, то все биты модуля числа инвертируются, то есть все единицы меняются на нули, а нули — на единицы, к инвертированному числу прибавляется единица, далее к результату дописывается знаковый разряд, равный единице. | *если число отрицательное, то все биты модуля числа инвертируются, то есть все единицы меняются на нули, а нули — на единицы, к инвертированному числу прибавляется единица, далее к результату дописывается знаковый разряд, равный единице. | ||
| − | В качестве примера переведём число <tex> -5 </tex> в дополнительный восьмибитный код. Прямой код модуля <tex> -5 </tex> | + | В качестве примера переведём число <tex> -5 </tex> в дополнительный восьмибитный код. Прямой код модуля <tex> -5 </tex>: <tex> 0000101 </tex>, обратный — <tex> 1111010 </tex>, прибавляем <tex> 1 </tex>, получаем <tex> 1111011 </tex>, приписываем <tex> 1 </tex> в качестве знакового разряда, в результате получаем <tex> 11111011 </tex>. |
Также дополнительный код отрицательного числа <tex> A </tex>, хранящегося в <tex> n </tex> битах, равен <tex> 2^n - |A| </tex>. По сути, дополнительный код представляет собой дополнение <tex> |A| </tex> до <tex> 0 </tex>: так как в <tex> n </tex>-разрядной арифметике <tex> 2^{n} = 0 </tex> (двоичная запись этого числа состоит из единицы и <tex> n </tex> нулей, а в <tex> n </tex>-разрядную ячейку помещаются только <tex> n </tex> младших разрядов, то есть <tex> n </tex> нулей), то верно равенство <tex> 2^n - |A| + |A| = 0 </tex>. | Также дополнительный код отрицательного числа <tex> A </tex>, хранящегося в <tex> n </tex> битах, равен <tex> 2^n - |A| </tex>. По сути, дополнительный код представляет собой дополнение <tex> |A| </tex> до <tex> 0 </tex>: так как в <tex> n </tex>-разрядной арифметике <tex> 2^{n} = 0 </tex> (двоичная запись этого числа состоит из единицы и <tex> n </tex> нулей, а в <tex> n </tex>-разрядную ячейку помещаются только <tex> n </tex> младших разрядов, то есть <tex> n </tex> нулей), то верно равенство <tex> 2^n - |A| + |A| = 0 </tex>. | ||
| Строка 88: | Строка 89: | ||
Можно получить диапазон значений <tex> [-2^{n-1}; 2^{n-1} - 1] </tex>. | Можно получить диапазон значений <tex> [-2^{n-1}; 2^{n-1} - 1] </tex>. | ||
| − | + | Дополнительный код также удобно использовать для вычислений в длинной арифметике. Для сложения чисел с разными знаками нужно сложить все биты, запоминая перенос. При сложении последних двух битов перенос нужно проигнорировать, чтобы число по длине получилось равным длиннейшему из слагаемых, знак определится автоматически. При сложении чисел с одинаковыми знаками нужно следовать такому же алгоритму, но, если последние два бита переноса будут разными, возникнет переполнение. В таком случае последний бит переноса откидывать не надо, и результат окажется на бит длиннее, чем длиннейшее из слагаемых. | |
| + | === Достоинства представления чисел с помощью кода с дополнением до двух === | ||
*возможность заменить арифметическую операцию вычитания операцией сложения и сделать операции сложения одинаковыми для знаковых и беззнаковых типов данных, что существенно упрощает архитектуру процессора и увеличивает его быстродействие; | *возможность заменить арифметическую операцию вычитания операцией сложения и сделать операции сложения одинаковыми для знаковых и беззнаковых типов данных, что существенно упрощает архитектуру процессора и увеличивает его быстродействие; | ||
*нет проблемы двух нулей. | *нет проблемы двух нулей. | ||
| − | + | === Недостатки представления чисел с помощью кода с дополнением до двух === | |
| − | *ряд положительных и отрицательных чисел несимметричен, но это не так важно: с помощью дополнительного кода выполнены гораздо более важные вещи, желаемые от способа представления целых чисел | + | *ряд положительных и отрицательных чисел несимметричен, но это не так важно: с помощью дополнительного кода выполнены гораздо более важные вещи, желаемые от способа представления целых чисел; |
*в отличие от сложения, числа в дополнительном коде нельзя сравнивать как беззнаковые, или вычитать без расширения разрядности. | *в отличие от сложения, числа в дополнительном коде нельзя сравнивать как беззнаковые, или вычитать без расширения разрядности. | ||
| − | == | + | Несмотря на недостатки, дополнение до двух в современных вычислительных системах используется чаще всего. |
| + | |||
| + | == См. также == | ||
| + | |||
| + | *[[Представление_вещественных_чисел | Представление вещественных чисел]] | ||
| + | *[[Представление_символов,_таблицы_кодировок | Представление символов, таблицы кодировок]] | ||
| + | |||
| + | == Источники информации == | ||
| + | |||
*Эндрю Таненбаум «Архитектура компьютера», 5-е изд., стр. 739—741 | *Эндрю Таненбаум «Архитектура компьютера», 5-е изд., стр. 739—741 | ||
| + | *[https://en.wikipedia.org/wiki/Signed_number_representations#Two.27s_complement Wikipedia — Signed number representations] | ||
| + | *[https://en.wikipedia.org/wiki/Offset_binary Wikipedia — Offset binary] | ||
| + | *[http://ru.wikipedia.org/wiki/Прямой_код Википедия — Прямой код] | ||
| + | *[http://ru.wikipedia.org/wiki/Дополнительный_код_(представление_числа) Википедия — Дополнительный код] | ||
| − | |||
| − | |||
| − | |||
| − | |||
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
[[Категория: Представление информации]] | [[Категория: Представление информации]] | ||
Версия 14:33, 29 ноября 2015
Выбор способа хранения целых чисел в памяти компьютера — не такая тривиальная задача, как могло бы показаться на первый взгляд. Желательно, чтобы этот способ:
- не требовал усложнения архитектуры процессора для выполнения арифметических операций с отрицательными числами;
- не усложнял арифметические действия;
- хранил бы одинаковое количество положительных и отрицательных чисел.
Рассмотрим разные методы представления.
Содержание
Прямой код
При записи числа в прямом коде (англ. Signed magnitude representation) старший разряд является знаковым разрядом. Если его значение равно нулю, то представлено положительное число или положительный ноль, если единице, то представлено отрицательное число или отрицательный ноль. В остальных разрядах (которые называются цифровыми) записывается двоичное представление модуля числа. Например, число в восьмибитном типе данных, использующем прямой код, будет выглядеть так: .
Таким способом в -битовом типе данных можно представить диапазон чисел .
Достоинства представления чисел с помощью прямого кода
- получить прямой код числа достаточно просто.
Недостатки представления чисел с помощью прямого кода
- выполнение арифметических операций с отрицательными числами требует усложнения архитектуры центрального процессора (например, для вычитания невозможно использовать сумматор, необходима отдельная схема для этого);
- существуют два нуля: и , из-за чего усложняется арифметическое сравнение.
Из-за весьма существенных недостатков прямой код используется очень редко.
Код со сдвигом
При использовании кода со сдвигом (англ. Offset binary) целочисленный отрезок от нуля до ( — количество бит) сдвигается влево на , а затем получившиеся на этом отрезке числа последовательно кодируются в порядке возрастания кодами от до . Например, число в восьмибитном типе данных, использующем код со сдвигом, превратится в , то есть будет выглядеть так: .
По сути, при таком кодировании:
- к кодируемому числу прибавляют ;
- переводят получившееся число в двоичную систему исчисления.
Можно получить диапазон значений .
Достоинства представления чисел с помощью кода со сдвигом
- не требуется усложнение архитектуры процессора;
- нет проблемы двух нулей.
Недостатки представления чисел с помощью кода со сдвигом
- при арифметических операциях нужно учитывать смещение, то есть проделывать на одно действие больше (например, после «обычного» сложения двух чисел у результата будет двойное смещение, одно из которых необходимо вычесть);
- ряд положительных и отрицательных чисел несимметричен.
Из-за необходимости усложнять арифметические операции код со сдвигом для представления целых чисел используется не часто, но зато применяется для хранения порядка вещественного числа.
Дополнительный код (дополнение до единицы)
В качестве альтернативы представления целых чисел может использоваться код с дополнением до единицы (англ. Ones' complement).
Алгоритм получения кода числа:
- если число положительное, то в старший разряд (который является знаковым) записывается ноль, а далее записывается само число;
- если число отрицательное, то код получается инвертированием представления модуля числа (получается обратный код);
- если число является нулем, от его можно представить двумя способами: или .
Пример: переведём число в двоичный восьмибитный код. Прямой код модуля : , инвертируем и получаем . Для получения из дополнительного кода самого числа достаточно инвертировать все разряды кода.
Таким способом можно получить диапазон значений .
Достоинства представления чисел с помощью кода с дополнением до единицы
- Простое получение кода отрицательных чисел.
Недостатки представления чисел с помощью кода с дополнением до единицы
- выполнение арифметических операций с отрицательными числами требует усложнения архитектуры центрального процессора;
- существуют два нуля: и .
Дополнительный код (дополнение до двух)
Чаще всего для представления отрицательных чисел используется код с дополнением до двух (англ. Two's complement).
Алгоритм получения дополнительного кода числа:
- если число неотрицательное, то в старший разряд записывается ноль, далее записывается само число;
- если число отрицательное, то все биты модуля числа инвертируются, то есть все единицы меняются на нули, а нули — на единицы, к инвертированному числу прибавляется единица, далее к результату дописывается знаковый разряд, равный единице.
В качестве примера переведём число в дополнительный восьмибитный код. Прямой код модуля : , обратный — , прибавляем , получаем , приписываем в качестве знакового разряда, в результате получаем .
Также дополнительный код отрицательного числа , хранящегося в битах, равен . По сути, дополнительный код представляет собой дополнение до : так как в -разрядной арифметике (двоичная запись этого числа состоит из единицы и нулей, а в -разрядную ячейку помещаются только младших разрядов, то есть нулей), то верно равенство .
Для получения из дополнительного кода самого числа нужно инвертировать все разряды кода и прибавить к нему единицу. Можно проверить правильность, сложив дополнительный код с самим числом: результат должен быть равен . Переведём обратно. Инвертируем — , прибавляем , получаем — модуль исходного числа . Проверим: .
Можно получить диапазон значений .
Дополнительный код также удобно использовать для вычислений в длинной арифметике. Для сложения чисел с разными знаками нужно сложить все биты, запоминая перенос. При сложении последних двух битов перенос нужно проигнорировать, чтобы число по длине получилось равным длиннейшему из слагаемых, знак определится автоматически. При сложении чисел с одинаковыми знаками нужно следовать такому же алгоритму, но, если последние два бита переноса будут разными, возникнет переполнение. В таком случае последний бит переноса откидывать не надо, и результат окажется на бит длиннее, чем длиннейшее из слагаемых.
Достоинства представления чисел с помощью кода с дополнением до двух
- возможность заменить арифметическую операцию вычитания операцией сложения и сделать операции сложения одинаковыми для знаковых и беззнаковых типов данных, что существенно упрощает архитектуру процессора и увеличивает его быстродействие;
- нет проблемы двух нулей.
Недостатки представления чисел с помощью кода с дополнением до двух
- ряд положительных и отрицательных чисел несимметричен, но это не так важно: с помощью дополнительного кода выполнены гораздо более важные вещи, желаемые от способа представления целых чисел;
- в отличие от сложения, числа в дополнительном коде нельзя сравнивать как беззнаковые, или вычитать без расширения разрядности.
Несмотря на недостатки, дополнение до двух в современных вычислительных системах используется чаще всего.
См. также
Источники информации
- Эндрю Таненбаум «Архитектура компьютера», 5-е изд., стр. 739—741
- Wikipedia — Signed number representations
- Wikipedia — Offset binary
- Википедия — Прямой код
- Википедия — Дополнительный код