Стековые машины, эквивалентность двухстековой машины МТ

Стековая машина

Рис. 1. k-стековая машина

Стековая машина является обобщением детерминированных МП-автоматов с использованием нескольких стеков вместо одного.
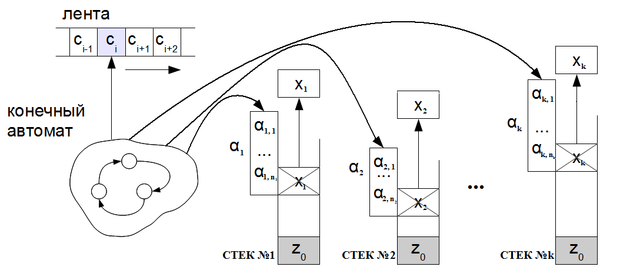
На рис. 1 изображена k-стековая машина. С ленты последовательно считываются символы входного алфавита ([math]c_i[/math] — текущий считываемый символ). В каждом стеке с вершины снимается символ [math]x_i[/math], вместо него помещается строка [math]\alpha_i[/math] таким образом, чтобы первый символ строки находился на вершине стека, и делается переход в автомате в зависимости от считанного с ленты символа [math]c_i[/math] и снятых со стеков верхних значений [math]x_i[/math]. Возможен также и [math]\varepsilon\[/math]-переход.

Определение:

[math]k[/math]-cтековой машиной называется набор A=[math]\langle\Sigma, \Gamma, Q, s\in Q, T \subset Q, z_0 \in \Gamma, \delta : Q \times \Sigma \cup \{\varepsilon\} \times \Gamma^k \rightarrow \cal P [/math] [math] (Q \times (\Gamma^*)^k)\rangle[/math], где [math]\Sigma[/math] — входной алфавит на ленте; [math]\Gamma[/math] — стековый алфавит; [math]Q[/math] — множество состояний автомата; [math]s[/math] — стартовое состояние автомата; [math]T[/math] — множество допускающих состояний автомата; [math]z_0[/math] — маркер дна стека; [math]\delta[/math] — функция переходов.

Эквивалентность двухстековой машины машине Тьюринга

Теорема:

Язык [math]L[/math] допускается машиной Тьюринга тогда и только тогда, когда он допускается двухстековой машиной.

Доказательство:

[math]\triangleright[/math]

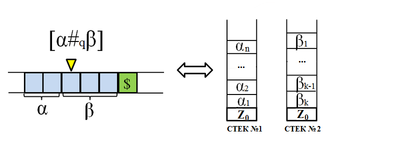
Для упрощения доказательства без умаления общности предположим, что вход для двухстековой машины заканчивается специальным символом [math]\$[/math], которого нет в исходном алфавите. Рис. 2. Представление ленты МТ двумя стеками и наоборот [math]\Rightarrow[/math] Докажем, что если язык [math]L[/math] допускается машиной Тьюринга, то он допускается двухстековой машиной. Мы будем имитировать ленту МТ двумя стеками (Рис. 2). В первом стеке будет хранится кусок ленты слева от положения головки, во втором стеке — справа, включая текущий символ. Разумеется, куски ленты хранятся без бесконечных цепочек пробелов, окружающих значащие символы ленты. Необходимо инициализировать стеки для того, чтобы их содержимое корректно отражало содержимое ленты МТ, поэтому строящаяся нами двухстековая машина сначала читает весь вход до конца (он помечен маркером [math]\$[/math]) и кладёт каждый новый поступивший символ на первый стек. Затем она перебрасывает все значения из первого стека во второй, таким образом получив пустой первый стек (что соответствует бесконечной цепочке пробелов слева от головки МТ) и второй стек, содержащий весь вход (что соответствует положению всех значащих символов ленты МТ не левее головки МТ). После этого машина перейдёт в начальное (имитируемое) состояние МТ. Теперь в каждый момент имитации мы будем знать текущий прочтённый головкой символ (им является вершина второго стека), и, соответственно, переход в МТ. Действие "[math]\leftarrow[/math]" МТ (сдвинуть головку влево) будем имитировать простым перекидыванием вершины первого стека на второй. Стоит обратить внимание на случай, когда первый стек перед действием был пуст, что говорило бы нам о том, что слева от головки бесконечная цепочка из пробелов. Поэтому такой переход имитируется добавлением на второй стек символа пробела и оставлением первого стека пустым. Аналогично делаются «сдвинуть головку вправо» и «остаться на месте». После имитации действия соответствующего перехода в МТ двухстековая машина делает переход в имитируемое новое состояние МТ. Допускающими состояниями двухстековой машины являются те, которые имитируют допускающие состояния МТ. Таким образом, мы с помощью двухстековой машины сымитировали МТ. [math]\Leftarrow[/math] Этот пункт доказательства аналогичен предыдущему. Содержимое двух стеков отображается лентой МТ так же, как и в предыдущем пункте (рис. 2). Снятие, например, с первого стека символа соответствует сдвигу куска ленты, соответствующего второму стеку, влево на одну позицию, что прекрасно умеет делать МТ. Положить символ на этот стек соответствует сдвигу куска ленты, соответствующего второму стеку, вправо на одну позицию, записи этого символа на место начального положения головки и сдвигу головки вправо на одну позицию (действие "положить цепочку на стек" аналогично последовательности действий "положить на стек один символ"). Операции со вторым стеком имитируются аналогично.

[math]\triangleleft[/math]

Источники информации

• Хопкрофт Д., Мотвани Р., Ульман Д. — Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. — Москва, Издательский дом «Вильямс», 2002. — 528 с. : ISBN 5-8459-0261-4 (рус.)