Алгоритм Хьюи — различия между версиями
Nikitaevg (обсуждение | вклад) (Новая страница: «{{Задача |definition=Дано ориентированное дерево, вершины которого раскрашены в цвета. Найти <t...») |
(нет различий)
|
Версия 22:27, 30 декабря 2015
| Задача: |
| Дано ориентированное дерево, вершины которого раскрашены в цвета. Найти , где число различных цветов в поддереве с корнем в вершине . Время работы: |
Алгоритм решения
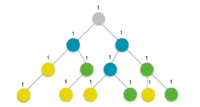
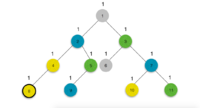
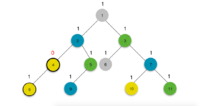
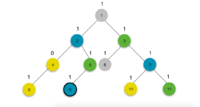
Для начала в каждой вершине поставим единицу. Теперь, если бы все вершины имели различные цвета, надо было бы пройти снизу вверх по дереву и просуммировать для каждой вершины числа, записанные в ее детях. Но некоторые вершины будут иметь одинаковые цвета, и это надо как-то учитывать. Для этого запустим обход в глубину. Также будем хранить для каждого цвета последнюю посещенную вершину данного цвета в массиве . Теперь, заходя в -ую вершину с цветом , смотрим: если вершина с таким цветом еще не встречалась, то просто записываем в , иначе, если вершина с данным цветом уже встречалась, то находим наименьшего общего предка данной вершины и последней вершины с таким цветом и вычитаем из их предка 1, и записываем в . Теперь при выходе из вершины можно просуммировать числа в ее детях и получить ответ для данной вершины, так как для нее все дети уже подсчитаны.
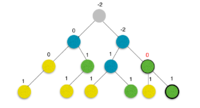
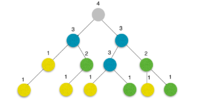
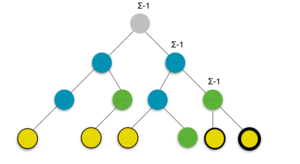
Пример:
Псевдокод
func dfs (Node v): used[v] := true for if !used[u] dfs(u) sum[v] := sum[v] + sum[u] if last[col[v]] != -1 sum[lca(v, last[col[v]])] -= 1 last[col[v]] := v func hugh (int n, int k, Node root): for used[v] := false sum[v] := 1 for k := 1 to k last[k] := -1 dfs (root)
Обоснование корректности
| Лемма: |
Наименьшим общим предком вершины и группы вершин, предшествующих по времени выхода, является наименьший общий предок данной вершины и последней, предшествующей ей из группы. |
| Доказательство: |
|
Рассмотрим дерево как последовательность букв, когда при входе в вершину или выходе из нее записывается ее буква. Пусть рассматриваемая вершина , а последняя рассмотренная из той же группы , их наименьший общий предок Рассмотрим два варианта расположения этих двух вершин. Теперь возьмем вершину , которая встречается до выхода из . Перебрав несложные пять случаев, можно легко убедиться, что наименьший общий предок и будет ниже, чем наименьший общий предок и . |
Для того, чтобы учитывать две вершины с одинаковым цветом, для каждой вершины требуется найти наименьшего общего предка этой вершины и вершин, предшествующих данной по времени выхода с таким же цветом и вычесть из значения этого предка 1. Так, при конечном подсчете значение наименьшего общего предка данной вершины и любой вершины, предшествующей данной с тем же цветом, уменьшится на единицу, так как наименьший предок этой точки и любой предшествующей того же цвета находится на пути из наименьшего общего предка всех этих вершин до корня. А как раз это и требуется - для каждой пары точек одного цвета учесть данный факт в их наименьшем общем предке. И по лемме, чтобы взять наименьшего общего предка текущей вершины и всех предшествующих вершин с данным цветом, надо взять наименьшего общего предка данной вершины и предыдущей вершины с данным цветом, он будет наименьшим для всех.