Задача об ожерельях

Задача:

Требуется посчитать количество ожерелий из $n$ бусинок, каждая из которых может быть покрашена в один из $k$ цветов. При сравнении двух ожерелий их можно поворачивать, но не переворачивать (т.е. разрешается сделать циклический сдвиг).

Решение этой задачи опирается на лемму Бёрнсайда и теорему Пойа.

Алгоритм решения задачи про ожерелья

Пусть нам даны бусинки $k$ различных цветов, а ожерелье должно состоять из $n$ бусинок.

Для решения воспользуемся формулой из теоремы Пойа.

$|C| =$ $\dfrac{1} {|G|}$$\sum\limits_{l \in G} k^{P(l)}$

По условию, перестановкой инвариантной данной будет любая перестановка, полученная из данной циклическим сдвигом. Очевидно, что для каждой перестановки длины $n$ существует ровно $n - 1$ инвариантная перестановка, то есть всего инвариантных перестановок в каждом классе $n$, теперь найдем $P(i)$. Заметим, что в $i$-ой перестановке на $l$-ой позиции стоит элемент $(i + l)\bmod n$. Также, заметим, что элемент $a$ переходит в элемент $a + in$, где $i = 1, 2, \ldots k$. Из этого следует, что длина цикла для $i$-ой перестановки равна $\dfrac{\mathrm{lcm}(n, i)}{i} = \dfrac{n}{\mathrm{gcd}(i,n)}$, где $\mathrm{gcd}(i, n)$ — НОД$(i, n)$, $\mathrm{lcm}(i, n)$ — НОК$(i, n)$. Откуда следует что:

$|C| =$ $\dfrac{1} {n}$$\sum\limits_{i = 1}^{n} k^{\mathrm{gcd}(i,n)}$.

где $|C|$ — кол-во различных ожерелий,которые можно составить из $n$ бусинок $k$ различных цветов.

Если раскраски ожерелья одинаковые, то они принадлежат одной орбите, т.е. одна получается из другой некоторым преобразованием симметрии. Неподвижные точки поворота есть только у тождественного поворота и их $n$ штук. Тогда, по лемме Бёрнсайда, число орбит равняется $\dfrac{n}{p}=\operatorname{gcd}(n,i)$, где $p$ минимальное число такое, что $ip$ делится на $n$, и число их раскрасок $N_i=k^{\operatorname{gcd}(n,i)}$. Сумма же инвариантных раскрасок для всех поворотов: $S=\sum\limits_{i=1}^{n}N_i=\sum\limits_{i=1}^{n}k^{\operatorname{gcd}(n,i)}$. В последней сумме $\varphi(n)$ слагаемых $(\varphi(n)$ — функция Эйлера$)$, для которых $\operatorname{gcd}(n,i)=1$. Если же $\operatorname{gcd}(n,i)=q$, то $\operatorname{gcd}\left(\dfrac{n}{q},\dfrac{i}{q}\right)=1$. Чтобы определить количество таких $i$, меньших $n$, нужно перебрать числа вида $i=lq,\,0\leqslant l\leqslant \dfrac{n}{q}$ и проверять их на условие $1=\operatorname{gcd}\left(\dfrac{n}{q},\dfrac{i}{q}\right)=\operatorname{gcd}\left(\dfrac{n}{q},l\right)$. Таких чисел, очевидно, $\varphi\left(\dfrac{n}{q}\right)$ (по определению $\varphi(n)$). Поэтому сумму можно заменить: $S=\sum\limits_{i=1}^{n}k^{\operatorname{gcd}(n,i)}=\sum\limits_{q|n}\varphi\left(\dfrac{n}{q}\right)k^q$.

Тогда $|C| =$ $\dfrac{1} {n}$$\sum\limits_{q|n}\varphi\left(\dfrac{n}{q}\right)k^q$.

Алгоритм решения задачи про ожерелья с отражениями

Слева пример оси для нечётного случая. Справа для чётного.

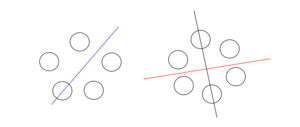
Пусть теперь ожерелья считаются одинаковыми, если они не только переходят друг в друга поворотом, но и отражением относительно некоторой оси (ось может проходить через две противоположные бусинки или через две противоположные пустоты в чётном случае и через бусинку и пустоту напротив неё в нечётном случае). Такие ожерелья называются bracelets . Будем пользоваться леммой Бёрнсайда. Разберём два случая.

Для начала покажем, что в качестве операций требуется рассматривать только повороты и отражения.

• Поворот и отражение — отражение.

Занумеруем наши бусинки по часовой стрелке. Поворот и отражение не меняют порядка (в каком-то направлении бусинки занумерованы по порядку). Нетрудно понять, что отражение меняет направление обхода наших бусинок и не меняет порядка. Если мы сначала сделаем поворот, а потом отразим относительно какой-нибудь оси, то мы то самое же можем получить и обыкновенным отражением относительно какой-то оси. Такая ось найдётся, потому что всегда можно выбрать ось, что поставит первую бусинку на своё изначальное место, поменяв направление обхода (если перебирать все оси подряд, начиная с оси, проходящей через нужную нам бусинку, то изначально она останется на своём месте, потом сместится на одно место, потом на два и.т.д.). Поэтому поворот и отражение не добавляет нам новой операции.

• Отражение и поворот — отражение.

Аналогичные рассуждения.

• Отражение и отражение — поворот.

Тут мы дважды меняем направление обхода, но не меняем порядка. Поэтому данная операция заменяется обычным поворотом.

Пусть число бусинок нечётное, тогда мы имеем $n$ осей, проходящих через каждую бусинку. Рассмотрим одну ось. Возьмём половину бусинок с одной стороны от оси и ту бусинку, через которую проходит данная ось. Мы можем окрасить их в произвольные цвета, а остальная половина по ним однозначно восстановится. Таким образом количество неподвижных точек для одной оси будет $k^{\frac{n + 1}{2}}$. Операций в группе будет в два раза больше, чем было: $2n$ ($n$ сдвигов и $n$ отражений).

По Лемме Бёрнсайда: $|B| =$ $\dfrac{1} {|G|}$$\sum\limits_{k \in G}I(k)$

$|G| = 2n$. Первые $n$ операций — повороты, и сумма количества их неподвижных точек, делённая на $2n$, принимает значение $\dfrac{|C|} {2}$, где $|C|$ - количество ожерелий из $n$ бусинок $k$ различных цветов без отражений (задача выше) т.к. деление в задаче без отражений происходило на $n$, а здесь на $2n$. Следующие $n$ операций — отражения. У каждой такой операции $k^{\frac{n + 1}{2}}$ неподвижных точек. Поэтому сумма получается $k^{\frac{n + 1}{2}}n$.

$|B| = \dfrac{|C|}{2} + \dfrac{1}{2n}k^{\dfrac{n + 1}{2}}n = \dfrac{|C|}{2} + \dfrac{1}{2}k^{\dfrac{n + 1}{2}}$$= \dfrac{1} {2n}\sum\limits_{q|n}\varphi\left(\dfrac{n}{q}\right)k^q + \dfrac{1}{2}k^{\dfrac{n + 1}{2}}$

Разберём теперь чётный случай. Тут мы имеем $\frac{n}{2}$ осей, проходящих через пустоты между бусинками (ось можно провести через пустоту после каждой бусинки, но половина из них будет повторяться). В таких вот случаях можно выбрать по $\frac{n}{2}$ бусинок и дать им произвольные цвета. Остальная половина восстановится по ним. Таким образом для данных осей количество неподвижных точек будет $k^{\frac{n}{2}}$. Ещё у нас есть $\frac{n}{2}$ осей, проходящих через бусинки. В данных случаях мы можем выбрать по $\frac{n}{2} + 1$ бусинок (бусинки на оси и все по одну какую-то сторону от неё). То есть будет $k^{\frac{n}{2} + 1}$ неподвижных точек. Операций также $2n$.

По Лемме Бёрнсайда:

$|B| = \dfrac{|C|}{2} + \dfrac{1}{2n}\left(\dfrac{n}{2}k^{\frac{n}{2}} + \dfrac{n}{2}k^{\frac{n}{2} + 1}\right)$ $= \dfrac{|C|}{2} + \dfrac{1}{4}k^{\frac{n}{2}}(k + 1) = \dfrac{1} {2n}\sum\limits_{q|n}\varphi\left(\dfrac{n}{q}\right)k^q + \dfrac{1}{4}k^{\frac{n}{2}}(k+1)$

См. также

• Лемма Бёрнсайда и Теорема Пойа
• Функция Эйлера

Источники информации

• Википедия — Теорема Редфилда — Пойа, Задача о количестве ожерелий
• MAXimal::algo::Ожерелья