Алгоритм Форда-Фалкерсона, реализация с помощью поиска в глубину — различия между версиями
(→Литература) |
|||
| Строка 2: | Строка 2: | ||
== Идея == | == Идея == | ||
| − | Идея алгоритма заключается в следующем. Изначально величине потока присваивается значение 0: <tex> f(u,v) = 0 </tex> для всех <tex> u, v </tex> из <tex> V </tex>. Затем величина потока итеративно увеличивается посредством поиска увеличивающего пути (путь от источника s к стоку t, вдоль которого можно послать ненулевой поток). В данной статье рассматривается алгоритм, осуществляющий этот поиск с помощью [[Обход в глубину, цвета вершин|обхода в глубину (dfs)]]. Процесс повторяется, пока можно найти увеличивающий путь. | + | Идея алгоритма заключается в следующем. Изначально величине потока присваивается значение <tex>0</tex>: <tex> f(u,v) = 0 </tex> для всех <tex> u, v </tex> из <tex> V </tex>. Затем величина потока итеративно увеличивается посредством поиска увеличивающего пути (путь от источника s к стоку t, вдоль которого можно послать ненулевой поток). В данной статье рассматривается алгоритм, осуществляющий этот поиск с помощью [[Обход в глубину, цвета вершин|обхода в глубину (dfs)]]. Процесс повторяется, пока можно найти увеличивающий путь. |
== Реализация == | == Реализация == | ||
| Строка 21: | Строка 21: | ||
== Оценка производительности == | == Оценка производительности == | ||
| − | Добавляя поток увеличивающего пути к уже имеющемуся потоку, максимальный поток будет получен, когда нельзя будет найти увеличивающий путь. Тем не менее, если величина пропускной способности — иррациональное число, то алгоритм может работать бесконечно. В целых числах таких проблем не возникает и время работы ограничено <tex>O(E|f|)</tex>, где <tex>E</tex> — число рёбер в графе, <tex>f</tex> — максимальный поток в графе, так как каждый увеличивающий путь может быть найден за <tex>O(E)</tex> и увеличивает поток как минимум на 1. | + | Добавляя поток увеличивающего пути к уже имеющемуся потоку, максимальный поток будет получен, когда нельзя будет найти увеличивающий путь. Тем не менее, если величина пропускной способности — иррациональное число, то алгоритм может работать бесконечно. В целых числах таких проблем не возникает и время работы ограничено <tex>O(E|f|)</tex>, где <tex>E</tex> — число рёбер в графе, <tex>f</tex> — максимальный поток в графе, так как каждый увеличивающий путь может быть найден за <tex>O(E)</tex> и увеличивает поток как минимум на <tex>1</tex>. |
| Строка 33: | Строка 33: | ||
! <tex>e_1</tex> !! <tex>e_2</tex> !! <tex>e_3</tex> | ! <tex>e_1</tex> !! <tex>e_2</tex> !! <tex>e_3</tex> | ||
|- | |- | ||
| − | | 0 || <tex>-</tex> || <tex>-</tex> || <tex>r^0=1</tex> || <tex>r</tex> || <tex>1</tex> | + | | <tex>0</tex> || <tex>-</tex> || <tex>-</tex> || <tex>r^0=1</tex> || <tex>r</tex> || <tex>1</tex> |
|- | |- | ||
| − | | 1 || <tex>\{ s, v_2, v_3, t \}</tex> || <tex>1</tex> || <tex>r^0</tex> || <tex>r^1</tex> || <tex>0</tex> | + | | <tex>1</tex> || <tex>\{ s, v_2, v_3, t \}</tex> || <tex>1</tex> || <tex>r^0</tex> || <tex>r^1</tex> || <tex>0</tex> |
|- | |- | ||
| − | | 2 || <tex>p_1</tex> || <tex>r^1</tex> || <tex>r^2</tex> || <tex>0</tex> || <tex>r^1</tex> | + | | <tex>2</tex> || <tex>p_1</tex> || <tex>r^1</tex> || <tex>r^2</tex> || <tex>0</tex> || <tex>r^1</tex> |
|- | |- | ||
| − | | 3 || <tex>p_2</tex> || <tex>r^1</tex> || <tex>r^2</tex> || <tex>r^1</tex> || <tex>0</tex> | + | | <tex>3</tex> || <tex>p_2</tex> || <tex>r^1</tex> || <tex>r^2</tex> || <tex>r^1</tex> || <tex>0</tex> |
|- | |- | ||
| − | | 4 || <tex>p_1</tex> || <tex>r^2</tex> || <tex>0</tex> || <tex>r^3</tex> || <tex>r^2</tex> | + | | <tex>4</tex> || <tex>p_1</tex> || <tex>r^2</tex> || <tex>0</tex> || <tex>r^3</tex> || <tex>r^2</tex> |
|- | |- | ||
| − | | 5 || <tex>p_3</tex> || <tex>r^2</tex> || <tex>r^2</tex> || <tex>r^3</tex> || <tex>0</tex> | + | | <tex>5</tex> || <tex>p_3</tex> || <tex>r^2</tex> || <tex>r^2</tex> || <tex>r^3</tex> || <tex>0</tex> |
|} | |} | ||
| − | Заметим, что после шага 1, как и после шага 5, остаточные способности рёбер <tex>e_1</tex>, <tex>e_2</tex> и <tex>e_3</tex> имеют форму <tex>r^n</tex>, <tex>r^{n+1}</tex> и <tex>0</tex>, соответственно, для какого-то натурального <tex>n</tex>. Это значит, что мы можем использовать увеличивающие пути <tex>p_1</tex>, <tex>p_2</tex>, <tex>p_1</tex> и <tex>p_3</tex> бесконечно много раз, и остаточные пропускные способности этих рёбер всегда будут в той же форме. Полный поток после шага 5 равен <tex>1 + 2(r^1 + r^2)</tex>. За бесконечное время полный поток сойдётся к <tex>\textstyle 1 + 2\sum_{i=1}^\infty r^i = 3 + 2r</tex>, тогда как максимальный поток равен <tex>2M + 1</tex>. Таким образом, алгоритм не только работает бесконечно долго, но даже и не сходится к оптимальному решению. | + | Заметим, что после шага <tex>1</tex>, как и после шага <tex>5</tex>, остаточные способности рёбер <tex>e_1</tex>, <tex>e_2</tex> и <tex>e_3</tex> имеют форму <tex>r^n</tex>, <tex>r^{n+1}</tex> и <tex>0</tex>, соответственно, для какого-то натурального <tex>n</tex>. Это значит, что мы можем использовать увеличивающие пути <tex>p_1</tex>, <tex>p_2</tex>, <tex>p_1</tex> и <tex>p_3</tex> бесконечно много раз, и остаточные пропускные способности этих рёбер всегда будут в той же форме. Полный поток после шага <tex>5</tex> равен <tex>1 + 2(r^1 + r^2)</tex>. За бесконечное время полный поток сойдётся к <tex>\textstyle 1 + 2\sum_{i=1}^\infty r^i = 3 + 2r</tex>, тогда как максимальный поток равен <tex>2M + 1</tex>. Таким образом, алгоритм не только работает бесконечно долго, но даже и не сходится к оптимальному решению. |
=== Пример медленной работы алгоритма Форда-Фалкерсона с использованием поиска в глубину по сравнению с реализацией, использующей поиск в ширину === | === Пример медленной работы алгоритма Форда-Фалкерсона с использованием поиска в глубину по сравнению с реализацией, использующей поиск в ширину === | ||
| − | При использовании поиска в ширину алгоритму потребуется всего лишь | + | При использовании поиска в ширину алгоритму потребуется всего лишь два шага. |
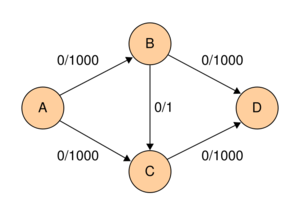
Дана сеть (рис. 2). | Дана сеть (рис. 2). | ||
[[Файл:F-f.1.png|thumb|300px|center|рис. 2]] | [[Файл:F-f.1.png|thumb|300px|center|рис. 2]] | ||
| Строка 55: | Строка 55: | ||
[[Файл:F-f.2.png|thumb|300px|center|рис. 3]] | [[Файл:F-f.2.png|thumb|300px|center|рис. 3]] | ||
[[Файл:F-f.3.png|thumb|300px|center|рис. 4]] | [[Файл:F-f.3.png|thumb|300px|center|рис. 4]] | ||
| − | рёбра <tex>AB, AC, BD, CD</tex> насытились лишь на 1. | + | рёбра <tex>AB, AC, BD, CD</tex> насытились лишь на <tex>1</tex>. |
Конечная сеть будет получена ещё через 1998 итераций (рис. 5). | Конечная сеть будет получена ещё через 1998 итераций (рис. 5). | ||
[[Файл:F-f.4.png|thumb|300px|center|рис. 5]] | [[Файл:F-f.4.png|thumb|300px|center|рис. 5]] | ||
| Строка 62: | Строка 62: | ||
* [[Теорема Форда-Фалкерсона]] | * [[Теорема Форда-Фалкерсона]] | ||
| − | == | + | == Источники информации == |
* [http://ru.wikipedia.org/wiki/Алгоритм_Форда_—_Фалкерсона Википедия: Алгоритм Форда — Фалкерсона] <br> | * [http://ru.wikipedia.org/wiki/Алгоритм_Форда_—_Фалкерсона Википедия: Алгоритм Форда — Фалкерсона] <br> | ||
* Томас Х. Кормен и др. Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1 | * Томас Х. Кормен и др. Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1 | ||
Версия 15:51, 13 января 2016
Алгоритм Форда-Фалкерсона — алгоритм, решающий задачу нахождения максимального потока в транспортной сети.
Содержание
Идея
Идея алгоритма заключается в следующем. Изначально величине потока присваивается значение : для всех из . Затем величина потока итеративно увеличивается посредством поиска увеличивающего пути (путь от источника s к стоку t, вдоль которого можно послать ненулевой поток). В данной статье рассматривается алгоритм, осуществляющий этот поиск с помощью обхода в глубину (dfs). Процесс повторяется, пока можно найти увеличивающий путь.
Реализация
dfs(u, Cmin) {
if (u = t)
return Cmin
u.vis <- true
for (uv in E)
if (!v.vis) && (uv.f < uv.c)
дельта <- dfs(v, min(Cmin, uv.c - uv.f))
if (дельта > 0) {
uv.f += дельта
uv.backEdge.f -= дельта
return дельта
}
return 0
}
Оценка производительности
Добавляя поток увеличивающего пути к уже имеющемуся потоку, максимальный поток будет получен, когда нельзя будет найти увеличивающий путь. Тем не менее, если величина пропускной способности — иррациональное число, то алгоритм может работать бесконечно. В целых числах таких проблем не возникает и время работы ограничено , где — число рёбер в графе, — максимальный поток в графе, так как каждый увеличивающий путь может быть найден за и увеличивает поток как минимум на .
Пример несходящегося алгоритма
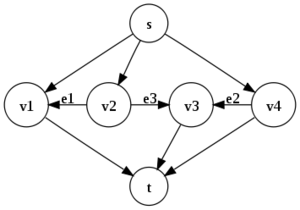
Рассмотрим приведённую справа сеть, с источником , стоком , пропускными способностями рёбер , и соответственно , и и пропускной способностью всех остальных рёбер, равной целому числу . Константа выбрана так, что . Мы используем пути из остаточного графа, приведённые в таблице, причём , и .
| Шаг | Найденный путь | Добавленный поток | Остаточные пропускные способности | ||
|---|---|---|---|---|---|
Заметим, что после шага , как и после шага , остаточные способности рёбер , и имеют форму , и , соответственно, для какого-то натурального . Это значит, что мы можем использовать увеличивающие пути , , и бесконечно много раз, и остаточные пропускные способности этих рёбер всегда будут в той же форме. Полный поток после шага равен . За бесконечное время полный поток сойдётся к , тогда как максимальный поток равен . Таким образом, алгоритм не только работает бесконечно долго, но даже и не сходится к оптимальному решению.
Пример медленной работы алгоритма Форда-Фалкерсона с использованием поиска в глубину по сравнению с реализацией, использующей поиск в ширину
При использовании поиска в ширину алгоритму потребуется всего лишь два шага. Дана сеть (рис. 2).
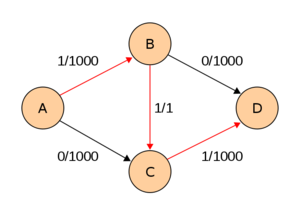
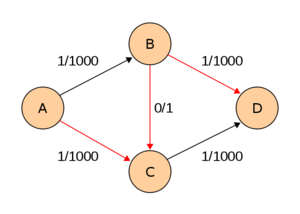
Благодаря двум итерациям (рис. 3 и рис. 4)
рёбра насытились лишь на . Конечная сеть будет получена ещё через 1998 итераций (рис. 5).
См. также
Источники информации
- Википедия: Алгоритм Форда — Фалкерсона
- Томас Х. Кормен и др. Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1