Игра «Жизнь» — различия между версиями
Mariashka (обсуждение | вклад) |
Mariashka (обсуждение | вклад) |
||
| Строка 43: | Строка 43: | ||
|statement= | |statement= | ||
Проблема останова игры «Жизнь» неразрешима. | Проблема останова игры «Жизнь» неразрешима. | ||
| − | |proof = Заметим, что если существует МТ, которая по начальной конфигурации игры «Жизнь» может определить, завершается ли она, то та же МТ может определить останавливается ли любая МТ, что противоречит неразрешимости проблемы останова для МТ. | + | |proof = |
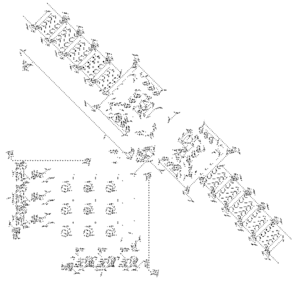
| + | [[Файл:TM.png|300px|thumb|right| МТ в игре «Жизнь»]] | ||
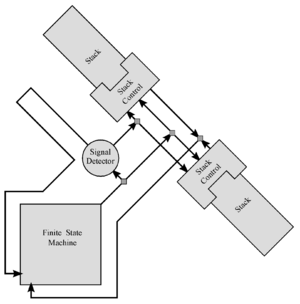
| + | [[Файл:TM_diagram.png|300px|thumb|right| Схема МТ в игре «Жизнь»]] | ||
| + | Заметим, что если существует МТ, которая по начальной конфигурации игры «Жизнь» может определить, завершается ли она, то та же МТ может определить останавливается ли любая МТ, что противоречит неразрешимости проблемы останова для МТ. | ||
<br> | <br> | ||
| − | Покажем схему построения МТ в игре Жизнь. | + | Покажем схему построения МТ в игре Жизнь (см.рисунок): |
| + | * конечный автомат, | ||
| + | * детектор сигнала, | ||
| + | * стек, | ||
| + | * контроллер стека. | ||
| + | |||
}} | }} | ||
== См.также == | == См.также == | ||
Версия 11:17, 14 января 2016
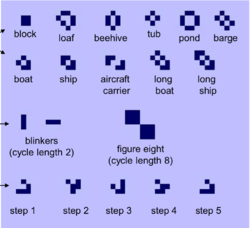
Игра «Жизнь» (англ. Conway's Game of Life) — клеточный автомат, придуманный английским математиком Джоном Конвеем в 1970.
Содержание
Правила
- Правило 1. Действие происходит на бесконечной плоскости, разделенной на клетки, которую можно иногда представить как зацикленную конечную.
- Правило 2. Каждая клетка может находиться в двух состояниях: быть живой или быть мёртвой.
- Правило 3. У каждой клетки соседей.
- Правило 4. Если клетка жива и у нее живых соседа, то она остается живой, иначе умирает.
- Правило 5. Если клетка мертва и у нее живых соседа, то она становится живой, иначе остается мертвой.
- Правило 6. Игра прекращается, если на поле не останется ни одной живой клетки.
- Правило 7. Игра прекращается, если при очередном шаге ни одна из клеток не меняет своего состояния.
- Правило 8. Игра прекращается, если конфигурация на очередном шаге в точности повторит себя же на одном из более ранних шагов.
Булевы функции
| Теорема: |
В игре «Жизнь» можно построить любую булеву функцию. |
| Доказательство: |
Базовые конструкцииРассмотрим базовые конструкции необходимые для построения.
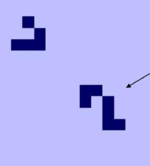
Булевы функцииТак как (штрих Шеффера или NAND) является полной системой, то достаточно построить и , чтобы показать возможность построения любой булевой функции. Построение NOTРассмотрим поток данных, состоящий из планеров. Наличие планера — , отсутствие — . Добавим поток планеров, состоящий только из . При столкновении планеры исчезают, следовательно на месте образуется и наоборот. Построение ANDСм. рисунок. Пусть , тогда y соударяется с . Если , то на выходе ничего не попадет, если , то просто пройдет . 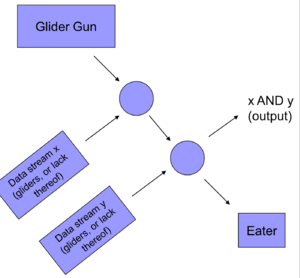 |
| Теорема: |
Проблема останова игры «Жизнь» неразрешима. |
| Доказательство: |
|
Заметим, что если существует МТ, которая по начальной конфигурации игры «Жизнь» может определить, завершается ли она, то та же МТ может определить останавливается ли любая МТ, что противоречит неразрешимости проблемы останова для МТ.
|
См.также
- Неразрешимость исчисления предикатов первого порядка
- Задача о выводе в полусистеме Туэ
- Задача о замощении
- Однозначность грамматики
- Неразрешимость задачи об эквивалентности КС-грамматик
- Неразрешимость проблемы существования решения диофантова уравнения в целых числах