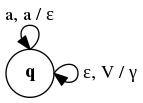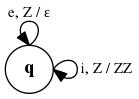Совпадение множества языков МП-автоматов и контекстно-свободных языков — различия между версиями
YanaZimka (обсуждение | вклад) |
YanaZimka (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| − | + | == Построение МП-автомата по заданной КС-грамматике == | |
{{Теорема | {{Теорема | ||
|id = th1 | |id = th1 | ||
| − | |statement = Класс [[Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора | контекстно-свободных языков]] | + | |statement = Класс [[Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора | контекстно-свободных языков]] <tex>(\mathrm{CFG})</tex> является подмножеством класса языков, задаваемых [[Автоматы с магазинной памятью | автоматами с магазинной памятью]] <tex>(\mathrm{PDA})</tex>, то есть по любой КС-грамматике можно построить МП-автомат, задающий тот же язык, что и исходная грамматика. |
|proof = | |proof = | ||
Пусть дана КС-грамматика <tex>\Gamma =\langle \Sigma, N, S, P\rangle</tex>. Поскольку классы языков, допускаемых МП-автоматами по допускающему состоянию и по пустому стеку, [[МП-автоматы, допуск по пустому стеку и по допускающему состоянию, эквивалентность | совпадают]], достаточно построить автомат с допуском по пустому стеку. | Пусть дана КС-грамматика <tex>\Gamma =\langle \Sigma, N, S, P\rangle</tex>. Поскольку классы языков, допускаемых МП-автоматами по допускающему состоянию и по пустому стеку, [[МП-автоматы, допуск по пустому стеку и по допускающему состоянию, эквивалентность | совпадают]], достаточно построить автомат с допуском по пустому стеку. | ||
| Строка 17: | Строка 17: | ||
;Пусть <tex>S \Rightarrow^* w</tex>.: Рассмотрим [[ Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора | левосторонний вывод ]] <tex>S = \gamma_0 \Rightarrow \gamma_1 \Rightarrow ... \Rightarrow \gamma_n=w</tex>. Обозначим как <tex>v_i</tex> наибольший префикс <tex>\gamma_i</tex>, состоящий только из терминалов, а <tex>\alpha_i</tex> {{---}} остаток <tex>\gamma_i</tex>, то есть <tex>\gamma_i = v_i\alpha_i</tex>, причём <tex>v_i \in \Sigma^*</tex>, а <tex>\alpha_i</tex> начинается с нетерминала (либо пустая). С помощью индукции по <tex>i</tex> докажем, что <tex>(q, w, S) \vdash^* (q, x_i, \alpha_i)</tex> для <tex>i \leq n</tex>, где <tex>x_i</tex> {{---}} то, что остаётся после чтения <tex>v_i</tex>, то есть <tex>v_ix_i = w</tex>. Иными словами, переходя по автомату по символам <tex>v_i</tex>, можно оставить на стеке <tex>\alpha_i</tex>. | ;Пусть <tex>S \Rightarrow^* w</tex>.: Рассмотрим [[ Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора | левосторонний вывод ]] <tex>S = \gamma_0 \Rightarrow \gamma_1 \Rightarrow ... \Rightarrow \gamma_n=w</tex>. Обозначим как <tex>v_i</tex> наибольший префикс <tex>\gamma_i</tex>, состоящий только из терминалов, а <tex>\alpha_i</tex> {{---}} остаток <tex>\gamma_i</tex>, то есть <tex>\gamma_i = v_i\alpha_i</tex>, причём <tex>v_i \in \Sigma^*</tex>, а <tex>\alpha_i</tex> начинается с нетерминала (либо пустая). С помощью индукции по <tex>i</tex> докажем, что <tex>(q, w, S) \vdash^* (q, x_i, \alpha_i)</tex> для <tex>i \leq n</tex>, где <tex>x_i</tex> {{---}} то, что остаётся после чтения <tex>v_i</tex>, то есть <tex>v_ix_i = w</tex>. Иными словами, переходя по автомату по символам <tex>v_i</tex>, можно оставить на стеке <tex>\alpha_i</tex>. | ||
| − | :* База | + | :* '''База:''' <br> Пусть <tex>i = 0</tex>. <br> В этом случае <tex>\gamma_0 = S</tex>, поэтому <tex>v_0 = \varepsilon, \alpha_0 = S, x_i = w</tex>. Очевидно, <tex>(q, w, S) \vdash^* (q, w, S)</tex>. |
| − | :* Индукционный переход: <br> Пусть <tex>(q, w, S) \vdash^* (q, x_i, \alpha_i)</tex> для <tex>i < n</tex>. <tex>\alpha_i</tex> по определению начинается с какого-то нетерминала <tex>V</tex> (если <tex>\alpha_i = \varepsilon</tex>, то получена <tex>\gamma_n</tex>, а мы предположили, что <tex>i < n</tex>), то есть <tex>\alpha_i = Vq_i</tex> Поскольку мы рассматриваем левосторонний вывод, то переход <tex>\gamma_i \Rightarrow \gamma_{i + 1}</tex> включает замену нетерминала <tex>V</tex> на какую-то цепочку <tex>\beta</tex> по правилу <tex>V \rightarrow \beta</tex>. Так как <tex>\gamma_i = v_i \alpha_i = v_i V q_i</tex>, то <tex>\gamma_{i + 1} = v_i \beta q_i = v_{i + 1} \alpha_{i + 1}</tex>. В автомате <tex>A</tex> по построению присутствует правило перехода <tex>\delta(q, \varepsilon, V) = \{(q, \beta)\}</tex>, поэтому <tex>\alpha_i</tex> на стеке можно заменить на <tex>\beta q_i</tex>. Заметим, что <tex>\beta q_i</tex> представляет собой конкатенацию нескольких терминалов из <tex>w</tex> и <tex>\alpha_{i + 1}</tex>. Считывая очередные символы строки <tex>w</tex>, будем переходить по автомату, убирая терминалы со стека, пока не встретим нетерминал. Таким образом, на стеке окажется <tex>\alpha_{i+1}</tex>. Получили, что <tex>(q, x_i, \alpha_i) \vdash^* (q, x_{i + 1}, \alpha_{i + 1})</tex>, а значит, <tex>(q, w, S) \vdash^* (q, x_{i + 1}, \alpha_{i + 1})</tex>. Индукционный переход доказан. | + | :* '''Индукционный переход:''' <br> Пусть <tex>(q, w, S) \vdash^* (q, x_i, \alpha_i)</tex> для <tex>i < n</tex>. <tex>\alpha_i</tex> по определению начинается с какого-то нетерминала <tex>V</tex> (если <tex>\alpha_i = \varepsilon</tex>, то получена <tex>\gamma_n</tex>, а мы предположили, что <tex>i < n</tex>), то есть <tex>\alpha_i = Vq_i</tex> Поскольку мы рассматриваем левосторонний вывод, то переход <tex>\gamma_i \Rightarrow \gamma_{i + 1}</tex> включает замену нетерминала <tex>V</tex> на какую-то цепочку <tex>\beta</tex> по правилу <tex>V \rightarrow \beta</tex>. Так как <tex>\gamma_i = v_i \alpha_i = v_i V q_i</tex>, то <tex>\gamma_{i + 1} = v_i \beta q_i = v_{i + 1} \alpha_{i + 1}</tex>. В автомате <tex>A</tex> по построению присутствует правило перехода <tex>\delta(q, \varepsilon, V) = \{(q, \beta)\}</tex>, поэтому <tex>\alpha_i</tex> на стеке можно заменить на <tex>\beta q_i</tex>. Заметим, что <tex>\beta q_i</tex> представляет собой конкатенацию нескольких терминалов из <tex>w</tex> и <tex>\alpha_{i + 1}</tex>. Считывая очередные символы строки <tex>w</tex>, будем переходить по автомату, убирая терминалы со стека, пока не встретим нетерминал. Таким образом, на стеке окажется <tex>\alpha_{i+1}</tex>. Получили, что <tex>(q, x_i, \alpha_i) \vdash^* (q, x_{i + 1}, \alpha_{i + 1})</tex>, а значит, <tex>(q, w, S) \vdash^* (q, x_{i + 1}, \alpha_{i + 1})</tex>. Индукционный переход доказан. |
: Заметим, что <tex>\alpha_n = \varepsilon, v_n = w, x_n = \varepsilon</tex>, поэтому <tex>(q, w, S) \vdash^* (q, \varepsilon, \varepsilon)</tex>. | : Заметим, что <tex>\alpha_n = \varepsilon, v_n = w, x_n = \varepsilon</tex>, поэтому <tex>(q, w, S) \vdash^* (q, \varepsilon, \varepsilon)</tex>. | ||
;Пусть <tex>(q, w, S) \vdash^* (q, \varepsilon, \varepsilon)</tex>.: Воспользуемся индукцией по числу переходов в автомате и докажем для любой строки <tex>x</tex> и нетерминала <tex>M \in N</tex>, что если <tex>(q, x, M) \vdash^* (q, \varepsilon, \varepsilon)</tex>, то <tex>M \Rightarrow^* x</tex>. | ;Пусть <tex>(q, w, S) \vdash^* (q, \varepsilon, \varepsilon)</tex>.: Воспользуемся индукцией по числу переходов в автомате и докажем для любой строки <tex>x</tex> и нетерминала <tex>M \in N</tex>, что если <tex>(q, x, M) \vdash^* (q, \varepsilon, \varepsilon)</tex>, то <tex>M \Rightarrow^* x</tex>. | ||
| − | :* База | + | :* '''База:''' <br> Пусть в автомате один переход. <br> Если <tex>(q, x, M) \vdash^* (q, \varepsilon, \varepsilon)</tex>, то <tex>x = \varepsilon</tex> и в грамматике присутствует правило <tex>M \rightarrow \varepsilon</tex>, по которому выводится <tex>\varepsilon = x</tex>. |
| − | :* Индукционный переход: <br> Предположим, что автомат <tex>A</tex> совершает <tex>n</tex> шагов (<tex>n > 1</tex>). Изначально на вершине стеке находится <tex>M</tex>, поэтому первый переход совершается по какому-то правилу из первого пункта построения <tex>\delta</tex>, и на стеке оказывается последовательность из терминалов и нетерминалов <tex>Y_1 Y_2 \ldots Y_k</tex>. В процессе следующих <tex>n - 1</tex> переходов автомат прочитает строку <tex>x</tex> и поочерёдно вытолкнет со стека <tex>Y_1 Y_2 \ldots Y_k</tex>. Разобьём <tex>w</tex> на подстроки <tex>x_1 x_2 \ldots x_k</tex>, где <tex>x_1</tex> {{---}} порция входа, прочитанная до выталкивания <tex>Y_1</tex> со стека, <tex>x_2</tex> {{---}} следующая порция входа, прочитанная до выталкивания <tex>Y_2</tex> со стека и так далее. Формально можно заключить, что <tex>(q, x_i x_{i + 1} \ldots x_k, Y_i) \vdash^* (q, x_{i + 1} \ldots x_k, \varepsilon)</tex>, причём менее чем за <tex>n</tex> шагов. Если <tex>Y_i</tex> {{---}} нетерминал, то по индукционному предположению имеем, что <tex>Y_i \Rightarrow^* x_i</tex>. Если же <tex>Y_i</tex> {{---}} терминал, то должен совершаться только один переход, в котором проверяется совпадение <tex>x_i</tex> и <tex>Y_i</tex>. Значит, <tex>Y_i \Rightarrow^* x_i</tex> за 0 шагов. <br> Таким образом, получаем, что <tex>M \Rightarrow Y_1 Y_2 \ldots Y_k \Rightarrow^* x_1 x_2 \ldots x_k = x</tex>. | + | :* '''Индукционный переход:''' <br> Предположим, что автомат <tex>A</tex> совершает <tex>n</tex> шагов (<tex>n > 1</tex>). Изначально на вершине стеке находится <tex>M</tex>, поэтому первый переход совершается по какому-то правилу из первого пункта построения <tex>\delta</tex>, и на стеке оказывается последовательность из терминалов и нетерминалов <tex>Y_1 Y_2 \ldots Y_k</tex>. В процессе следующих <tex>n - 1</tex> переходов автомат прочитает строку <tex>x</tex> и поочерёдно вытолкнет со стека <tex>Y_1 Y_2 \ldots Y_k</tex>. Разобьём <tex>w</tex> на подстроки <tex>x_1 x_2 \ldots x_k</tex>, где <tex>x_1</tex> {{---}} порция входа, прочитанная до выталкивания <tex>Y_1</tex> со стека, <tex>x_2</tex> {{---}} следующая порция входа, прочитанная до выталкивания <tex>Y_2</tex> со стека и так далее. Формально можно заключить, что <tex>(q, x_i x_{i + 1} \ldots x_k, Y_i) \vdash^* (q, x_{i + 1} \ldots x_k, \varepsilon)</tex>, причём менее чем за <tex>n</tex> шагов. Если <tex>Y_i</tex> {{---}} нетерминал, то по индукционному предположению имеем, что <tex>Y_i \Rightarrow^* x_i</tex>. Если же <tex>Y_i</tex> {{---}} терминал, то должен совершаться только один переход, в котором проверяется совпадение <tex>x_i</tex> и <tex>Y_i</tex>. Значит, <tex>Y_i \Rightarrow^* x_i</tex> за 0 шагов. <br> Таким образом, получаем, что <tex>M \Rightarrow Y_1 Y_2 \ldots Y_k \Rightarrow^* x_1 x_2 \ldots x_k = x</tex>. |
: Подставляя <tex>w</tex> вместо <tex>x</tex> и <tex>S</tex> вместо <tex>M</tex>, получаем, что <tex>S \Rightarrow^* w. | : Подставляя <tex>w</tex> вместо <tex>x</tex> и <tex>S</tex> вместо <tex>M</tex>, получаем, что <tex>S \Rightarrow^* w. | ||
</tex> | </tex> | ||
}} | }} | ||
| − | + | === Пример === | |
Поскольку доказательство теоремы конструктивно, то используя правила перехода, описанные в ней, можно преобразовать любую КС-грамматику в МП-автомат. Рассмотрим грамматику слов над алфавитом <tex>\{0, 1\}</tex>, в которых одинаковое количество нулей и единиц: | Поскольку доказательство теоремы конструктивно, то используя правила перехода, описанные в ней, можно преобразовать любую КС-грамматику в МП-автомат. Рассмотрим грамматику слов над алфавитом <tex>\{0, 1\}</tex>, в которых одинаковое количество нулей и единиц: | ||
: <tex> S \rightarrow 0S1 </tex>; | : <tex> S \rightarrow 0S1 </tex>; | ||
| Строка 42: | Строка 42: | ||
[[Файл:Example1.png]] | [[Файл:Example1.png]] | ||
| − | + | == Построение КС-грамматики по МП-автомату == | |
{{Теорема | {{Теорема | ||
|id = th2 | |id = th2 | ||
| − | |statement = Класс языков, задаваемых автоматами с магазинной памятью | + | |statement = Класс языков, задаваемых автоматами с магазинной памятью <tex>(\mathrm{PDA})</tex>, является подмножеством класса контекстно-свободных языков <tex>(\mathrm{CFG})</tex>, то есть по любому МП-автомату можно построить КС-грамматику, задающую тот же язык, что и допускаемый автоматом. |
|proof = | |proof = | ||
Пусть дан МП-автомат с допуском по пустому стеку <tex>A = \langle \Sigma, \Pi, Q, q_0 \in Q, z_0, \delta \rangle</tex>. Как отмечалось ранее, предположение о допуске по пустому стеку не умаляет общности. | Пусть дан МП-автомат с допуском по пустому стеку <tex>A = \langle \Sigma, \Pi, Q, q_0 \in Q, z_0, \delta \rangle</tex>. Как отмечалось ранее, предположение о допуске по пустому стеку не умаляет общности. | ||
| Строка 58: | Строка 58: | ||
;Пусть <tex>(p, w, X) \vdash^* (q, \varepsilon, \varepsilon)</tex>.: Докажем, что <tex>[pXq] \Rightarrow^* w</tex>, используя индукцию по числу переходов в автомате. | ;Пусть <tex>(p, w, X) \vdash^* (q, \varepsilon, \varepsilon)</tex>.: Докажем, что <tex>[pXq] \Rightarrow^* w</tex>, используя индукцию по числу переходов в автомате. | ||
| − | :*База | + | :*'''База:'''<br> Пусть выполняется только один переход.<br> Тогда длина <tex>w</tex> не больше единицы и <tex>(q, \varepsilon) \in \delta(p, w, X)</tex>, поэтому правило <tex>[pXq] \rightarrow w</tex> по построению должно присутствовать в <tex>P</tex>. |
| − | :*Индукционный переход:<br> Предположим, что <tex>(p, w, X) \vdash^* (q, \varepsilon, \varepsilon)</tex> за <tex>n > 1</tex> шагов. Первый переход имеет вид <tex>(p, w, X) \vdash (r_0, x, \gamma_1 \gamma_2 \ldots \gamma_k) \vdash^* (q, \varepsilon, \varepsilon)</tex>, где <tex>w = ax</tex> (<tex>a</tex> {{---}} символ из <tex>\Sigma</tex> или <tex>\varepsilon</tex>). Значит, <tex>(r_0, \gamma_1 \gamma_2 \ldots \gamma_k) \in \delta(p, a, X)</tex>. По построению в грамматике должно присутствовать правило <tex>[p X r_k] \rightarrow a [r_0 \gamma_1 r_1] [r_1 \gamma_2 r_2] \ldots [r_{k - 1} \gamma_k r_k]</tex> для любой последовательности состояний <tex>[r_1, \ldots r_k]</tex>. Пусть <tex>x = w_1 w_2 \ldots w_k</tex>, где <tex>w_i</tex> {{---}} входная цепочка, которая прочитывается до удаления <tex>\gamma_i</tex> со стека, то есть найдётся такая последовательность состояний <tex>[r_1, \ldots r_k]</tex>, что <tex>(r_{i - 1}, w_i, \gamma_i) \vdash^* (r_i, \varepsilon, \varepsilon)</tex>, причём заканчивается всё в <tex>q = r_k</tex>. Заметим, что все эти выводы содержат менее <tex>n</tex> переходов, а значит, по индукционному предположению <tex>[r_{i - 1} \gamma_i r_i] \Rightarrow^* w_i</tex> для всех <tex>i</tex>. <br> Собирая вышесказанное, получаем <tex>[p X r_k] \Rightarrow a [r_0 \gamma_1 r_1] [r_1 \gamma_2 r_2] \ldots [r_{k - 1} \gamma_k r_k] \Rightarrow^* a w_1 w_2 \ldots w_k = w</tex>. Так как <tex>r_k = q</tex>, то <tex>[pXq] \Rightarrow^* w</tex>, тем самым индукционный переход доказан. | + | :*'''Индукционный переход:'''<br> Предположим, что <tex>(p, w, X) \vdash^* (q, \varepsilon, \varepsilon)</tex> за <tex>n > 1</tex> шагов. Первый переход имеет вид <tex>(p, w, X) \vdash (r_0, x, \gamma_1 \gamma_2 \ldots \gamma_k) \vdash^* (q, \varepsilon, \varepsilon)</tex>, где <tex>w = ax</tex> (<tex>a</tex> {{---}} символ из <tex>\Sigma</tex> или <tex>\varepsilon</tex>). Значит, <tex>(r_0, \gamma_1 \gamma_2 \ldots \gamma_k) \in \delta(p, a, X)</tex>. По построению в грамматике должно присутствовать правило <tex>[p X r_k] \rightarrow a [r_0 \gamma_1 r_1] [r_1 \gamma_2 r_2] \ldots [r_{k - 1} \gamma_k r_k]</tex> для любой последовательности состояний <tex>[r_1, \ldots r_k]</tex>. Пусть <tex>x = w_1 w_2 \ldots w_k</tex>, где <tex>w_i</tex> {{---}} входная цепочка, которая прочитывается до удаления <tex>\gamma_i</tex> со стека, то есть найдётся такая последовательность состояний <tex>[r_1, \ldots r_k]</tex>, что <tex>(r_{i - 1}, w_i, \gamma_i) \vdash^* (r_i, \varepsilon, \varepsilon)</tex>, причём заканчивается всё в <tex>q = r_k</tex>. Заметим, что все эти выводы содержат менее <tex>n</tex> переходов, а значит, по индукционному предположению <tex>[r_{i - 1} \gamma_i r_i] \Rightarrow^* w_i</tex> для всех <tex>i</tex>. <br> Собирая вышесказанное, получаем <tex>[p X r_k] \Rightarrow a [r_0 \gamma_1 r_1] [r_1 \gamma_2 r_2] \ldots [r_{k - 1} \gamma_k r_k] \Rightarrow^* a w_1 w_2 \ldots w_k = w</tex>. Так как <tex>r_k = q</tex>, то <tex>[pXq] \Rightarrow^* w</tex>, тем самым индукционный переход доказан. |
;Пусть <tex>[pXq] \Rightarrow^* w</tex>.: Докажем, что <tex>(p, w, X) \vdash^* (q, \varepsilon, \varepsilon)</tex>, используя индукцию по числу шагов в порождении. | ;Пусть <tex>[pXq] \Rightarrow^* w</tex>.: Докажем, что <tex>(p, w, X) \vdash^* (q, \varepsilon, \varepsilon)</tex>, используя индукцию по числу шагов в порождении. | ||
| − | :*База | + | :*'''База:''' <br> Пусть <tex>[pXq] \Rightarrow^* w</tex> за один шаг.<br> Тогда в <tex>\Gamma</tex> должно быть правило вывода <tex>[pXq] \rightarrow w</tex>, а значит, в автомате должен быть переход <tex>(q, \varepsilon) \in \delta(p, w, X)</tex> и <tex>w</tex> не может иметь длину больше единицы. Таким образом, <tex>(p, w, X) \vdash^* (q, \varepsilon, \varepsilon)</tex>. |
| − | :*Индукционный переход: <br> Предположим, что <tex>[pXq] \Rightarrow^* w </tex> за <tex>n > 1</tex> шагов. По построению вывод должен иметь вид <tex>[p X r_k] \Rightarrow a [r_0 \gamma_1 r_1] [r_1 \gamma_2 r_2] \ldots [r_{k - 1} \gamma_k r_k] \Rightarrow^* w</tex>, где <tex>r_k = q</tex> и <tex>(r_0, \gamma_1 \gamma_2 \ldots \gamma_k) \in \delta(p, a, X)</tex>. Вновь представим <tex>w</tex> в виде <tex>w = a w_1 w_2 \ldots w_k</tex> так, что <tex>[r_{i - 1} \gamma_i r_i] \Rightarrow^* w_i</tex>. Так как все эти выводы содержат менее <tex>n</tex> шагов, то по индукционному предположению для всех <tex>i</tex> выполнено <tex>(r_{i - 1}, w_i, \gamma_i) \vdash^* (r_i, \varepsilon, \varepsilon)</tex>. Собирая всё вместе, получаем <tex>(r_0, w_1 w_2 \ldots w_k, \gamma_1 \gamma_2 \ldots \gamma_k) \vdash^* (r_1, w_2 w_3 \ldots w_k, \gamma_2 \gamma_3 \ldots \gamma_k) \vdash^* \ldots \vdash^* (r_k, \varepsilon, \varepsilon)</tex>. Так как <tex>(r_0, \gamma_1 \gamma_2 \ldots \gamma_k) \in \delta(p, a, X)</tex> и <tex>r_k = q</tex>, то в итоге <tex>(p, w, X) \vdash^* (q, \varepsilon, \varepsilon)</tex>. | + | :*'''Индукционный переход:''' <br> Предположим, что <tex>[pXq] \Rightarrow^* w </tex> за <tex>n > 1</tex> шагов. По построению вывод должен иметь вид <tex>[p X r_k] \Rightarrow a [r_0 \gamma_1 r_1] [r_1 \gamma_2 r_2] \ldots [r_{k - 1} \gamma_k r_k] \Rightarrow^* w</tex>, где <tex>r_k = q</tex> и <tex>(r_0, \gamma_1 \gamma_2 \ldots \gamma_k) \in \delta(p, a, X)</tex>. Вновь представим <tex>w</tex> в виде <tex>w = a w_1 w_2 \ldots w_k</tex> так, что <tex>[r_{i - 1} \gamma_i r_i] \Rightarrow^* w_i</tex>. Так как все эти выводы содержат менее <tex>n</tex> шагов, то по индукционному предположению для всех <tex>i</tex> выполнено <tex>(r_{i - 1}, w_i, \gamma_i) \vdash^* (r_i, \varepsilon, \varepsilon)</tex>. Собирая всё вместе, получаем <tex>(r_0, w_1 w_2 \ldots w_k, \gamma_1 \gamma_2 \ldots \gamma_k) \vdash^* (r_1, w_2 w_3 \ldots w_k, \gamma_2 \gamma_3 \ldots \gamma_k) \vdash^* \ldots \vdash^* (r_k, \varepsilon, \varepsilon)</tex>. Так как <tex>(r_0, \gamma_1 \gamma_2 \ldots \gamma_k) \in \delta(p, a, X)</tex> и <tex>r_k = q</tex>, то в итоге <tex>(p, w, X) \vdash^* (q, \varepsilon, \varepsilon)</tex>. |
Таким образом, мы доказали, что <tex>[pXq] \Rightarrow^* w \iff (p, w, X) \vdash^* (q, \varepsilon, \varepsilon)</tex>. Заметим, что <tex>S \Rightarrow^* w</tex> тогда и только тогда, когда найдётся <tex>p</tex>, что <tex>[q_0 z_0 p] \Rightarrow^* w</tex>. По доказанному выше это равносильно тому, что <tex>(q_0, w, z_0) \vdash^* (p, \varepsilon, \varepsilon)</tex>, то есть что <tex>A</tex> допускает <tex>w</tex> по пустому стеку. Суммируя всё вышесказанное, получаем, что построенная грамматика <tex>\Gamma</tex> порождает слово <tex>w</tex> тогда и только тогда, когда оно допускается автоматом <tex>A</tex>. | Таким образом, мы доказали, что <tex>[pXq] \Rightarrow^* w \iff (p, w, X) \vdash^* (q, \varepsilon, \varepsilon)</tex>. Заметим, что <tex>S \Rightarrow^* w</tex> тогда и только тогда, когда найдётся <tex>p</tex>, что <tex>[q_0 z_0 p] \Rightarrow^* w</tex>. По доказанному выше это равносильно тому, что <tex>(q_0, w, z_0) \vdash^* (p, \varepsilon, \varepsilon)</tex>, то есть что <tex>A</tex> допускает <tex>w</tex> по пустому стеку. Суммируя всё вышесказанное, получаем, что построенная грамматика <tex>\Gamma</tex> порождает слово <tex>w</tex> тогда и только тогда, когда оно допускается автоматом <tex>A</tex>. | ||
}} | }} | ||
| − | + | === Пример === | |
Пусть у нас имеется МП-автомат <tex>A = \langle \{i,e\}, \{Z\}, \{q\}, q, Z, \delta \rangle</tex>, функция <tex>\delta</tex> задана следующим образом: | Пусть у нас имеется МП-автомат <tex>A = \langle \{i,e\}, \{Z\}, \{q\}, q, Z, \delta \rangle</tex>, функция <tex>\delta</tex> задана следующим образом: | ||
| − | + | :<tex>\delta(q, i, Z) = \{(q, ZZ)\}</tex>, | |
| − | + | :<tex>\delta(q, e, Z) = \{(q, \varepsilon)\}</tex>. | |
[[Файл:Example2.png]] | [[Файл:Example2.png]] | ||
| Строка 77: | Строка 77: | ||
Так как стековый алфавит <tex>A</tex> содержит лишь один символ и одно состояние, то в построенной грамматике будет лишь 2 нетерминала: | Так как стековый алфавит <tex>A</tex> содержит лишь один символ и одно состояние, то в построенной грамматике будет лишь 2 нетерминала: | ||
| − | * <tex>S</tex> — стартовый нетерминал. | + | *<tex>S</tex> — стартовый нетерминал. |
| − | * <tex>[qZq]</tex> — единственная тройка, которую можно собрать из состояний автомата и символов стекового алфавита. | + | *<tex>[qZq]</tex> — единственная тройка, которую можно собрать из состояний автомата и символов стекового алфавита. |
Также грамматика имеет следующие правила вывода: | Также грамматика имеет следующие правила вывода: | ||
| Строка 86: | Строка 86: | ||
* Из <tex>\delta(q,e,Z)=\{(q,\varepsilon)\}</tex> получаем правило вывода <tex>[qZq] \rightarrow e</tex> | * Из <tex>\delta(q,e,Z)=\{(q,\varepsilon)\}</tex> получаем правило вывода <tex>[qZq] \rightarrow e</tex> | ||
Для удобства тройку <tex>[qZq]</tex> можно заменить символом <tex>A</tex>, в таком случае правила вывода в грамматике будут следующие: | Для удобства тройку <tex>[qZq]</tex> можно заменить символом <tex>A</tex>, в таком случае правила вывода в грамматике будут следующие: | ||
| − | + | :<tex>S \rightarrow A</tex>; | |
| − | + | :<tex>A \rightarrow iAA</tex>; | |
| − | + | :<tex>A \rightarrow e</tex>. | |
Упростим грамматику, заменив <tex>A</tex> на <tex>S</tex> (очевидно, она не поменяется), и получим в результате <tex>\Gamma = \langle\{i,e\}, \{S\}, S, \{S \rightarrow iSS | e\}\rangle</tex> | Упростим грамматику, заменив <tex>A</tex> на <tex>S</tex> (очевидно, она не поменяется), и получим в результате <tex>\Gamma = \langle\{i,e\}, \{S\}, S, \{S \rightarrow iSS | e\}\rangle</tex> | ||
| − | + | == Эквивалентность языков МП-автоматов и КС-языков== | |
{{Теорема | {{Теорема | ||
|about = об эквивалентности языков МП-автоматов и КС-языков | |about = об эквивалентности языков МП-автоматов и КС-языков | ||
| Строка 98: | Строка 98: | ||
}} | }} | ||
| − | + | == Следствия == | |
{{Утверждение | {{Утверждение | ||
|statement = Для любого МП-автомата с допуском по пустому стеку существует эквивалентный МП-автомат с одним состоянием. | |statement = Для любого МП-автомата с допуском по пустому стеку существует эквивалентный МП-автомат с одним состоянием. | ||
| Строка 113: | Строка 113: | ||
|proof = Построим КС-грамматику по данному автомату, затем по полученной грамматике построим МП-автомат, как указано выше. Заметим, что этот автомат не будет иметь <tex>\varepsilon</tex>-переходов, что и требовалось доказать. | |proof = Построим КС-грамматику по данному автомату, затем по полученной грамматике построим МП-автомат, как указано выше. Заметим, что этот автомат не будет иметь <tex>\varepsilon</tex>-переходов, что и требовалось доказать. | ||
}} | }} | ||
| − | === | + | == См. также == |
| − | |||
| − | |||
| − | |||
*[[Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора | Контекстно-свободные грамматики]] | *[[Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора | Контекстно-свободные грамматики]] | ||
*[[Автоматы с магазинной памятью | Автоматы с магазинной памятью]] | *[[Автоматы с магазинной памятью | Автоматы с магазинной памятью]] | ||
| − | == | + | == Источники информации == |
| + | *[https://en.wikipedia.org/wiki/Pushdown_automaton#PDA_and_context-free_languages Wikipedia — PDA and context-free languages] | ||
* Введение в теорию автоматов, языков и вычислений / Хопкрофт Д., Мотвани Р., Ульман Д. — М.:Издательский дом «Вильямс», 2002. с. 251. — ISBN 5-8459-0261-4 | * Введение в теорию автоматов, языков и вычислений / Хопкрофт Д., Мотвани Р., Ульман Д. — М.:Издательский дом «Вильямс», 2002. с. 251. — ISBN 5-8459-0261-4 | ||
Версия 17:49, 15 марта 2016
Содержание
Построение МП-автомата по заданной КС-грамматике
| Теорема: |
Класс контекстно-свободных языков является подмножеством класса языков, задаваемых автоматами с магазинной памятью , то есть по любой КС-грамматике можно построить МП-автомат, задающий тот же язык, что и исходная грамматика. |
| Доказательство: |
|
Пусть дана КС-грамматика . Поскольку классы языков, допускаемых МП-автоматами по допускающему состоянию и по пустому стеку, совпадают, достаточно построить автомат с допуском по пустому стеку. Построим автомат из одного состояния с входным алфавитом , стековым алфавитом , маркером дна и функцией перехода , определённой ниже. Формально , где задаётся следующим образом:
Покажем, что язык, допускаемый автоматом , совпадает с языком грамматики , то есть что :
|
Пример
Поскольку доказательство теоремы конструктивно, то используя правила перехода, описанные в ней, можно преобразовать любую КС-грамматику в МП-автомат. Рассмотрим грамматику слов над алфавитом , в которых одинаковое количество нулей и единиц:
- ;
- ;
- .
Множеством терминалов является , а нетерминалов — . Таким образом, стековый алфавит состоит из . Функция переходов определена следующим образом:
- (в соответствии с первым пунктом построения );
- ; (в соответствии со вторым пунктом построения ).
Построение КС-грамматики по МП-автомату
| Теорема: |
Класс языков, задаваемых автоматами с магазинной памятью , является подмножеством класса контекстно-свободных языков , то есть по любому МП-автомату можно построить КС-грамматику, задающую тот же язык, что и допускаемый автоматом. |
| Доказательство: |
|
Пусть дан МП-автомат с допуском по пустому стеку . Как отмечалось ранее, предположение о допуске по пустому стеку не умаляет общности. Построим эквивалентную ему КС-грамматику . В качестве нетерминалов будем использовать конструкции вида (где , ), которая неформально означает, что в процессе изменения состояния автомата от до символ удаляется с вершины стека, не затрагивая то, что находится ниже. Также введём стартовый нетерминал . Таким образом, . Правила вывода построим следующим образом:
Нетерминал должен выводить только те строки , которые переводят автомат из состояния в . Формально это можно записать следующим образом: . Докажем это утверждение:
|
Пример
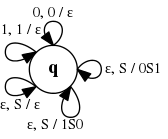
Пусть у нас имеется МП-автомат , функция задана следующим образом:
- ,
- .
Так как стековый алфавит содержит лишь один символ и одно состояние, то в построенной грамматике будет лишь 2 нетерминала:
- — стартовый нетерминал.
- — единственная тройка, которую можно собрать из состояний автомата и символов стекового алфавита.
Также грамматика имеет следующие правила вывода:
- Единственной продукцией для является . Но если бы у автомата было состояний, то тут бы имелось и продукций.
- Из того факта, что содержит , получаем правило вывода . Если бы у автомата было состояний, то такой переход порождал бы продукций.
- Из получаем правило вывода
Для удобства тройку можно заменить символом , в таком случае правила вывода в грамматике будут следующие:
- ;
- ;
- .
Упростим грамматику, заменив на (очевидно, она не поменяется), и получим в результате
Эквивалентность языков МП-автоматов и КС-языков
| Теорема (об эквивалентности языков МП-автоматов и КС-языков): |
Множество языков, допускаемых МП-автоматами, совпадает с множеством контекстно-свободных языков. |
| Доказательство: |
| Первая теорема гласит, что , а вторая — что . Таким образом, . |
Следствия
| Утверждение: |
Для любого МП-автомата с допуском по пустому стеку существует эквивалентный МП-автомат с одним состоянием. |
| Построим КС-грамматику по данному автомату, затем по полученной грамматике построим МП-автомат, как указано выше. Заметим, что этот автомат будет иметь одно состояние, что и требовалось доказать. |
| Утверждение: |
Для любого МП-автомата с допуском по пустому стеку существует эквивалентный МП-автомат, в любом переходе которого на стек кладётся не больше двух символов. |
| Построим КС-грамматику по данному автомату и приведём её к нормальной форме Хомского. Затем по полученной грамматике построим МП-автомат, как указано выше. Заметим, что в нормальной форме Хомского правые части всех правил имеют длину не больше двух, поэтому в любом переходе в полученном автомате на стек кладётся не больше двух символов. |
| Утверждение: |
Для любого МП-автомата существует эквивалентный МП-автомат с допуском по пустому стеку без -переходов. |
| Построим КС-грамматику по данному автомату, затем по полученной грамматике построим МП-автомат, как указано выше. Заметим, что этот автомат не будет иметь -переходов, что и требовалось доказать. |
См. также
Источники информации
- Wikipedia — PDA and context-free languages
- Введение в теорию автоматов, языков и вычислений / Хопкрофт Д., Мотвани Р., Ульман Д. — М.:Издательский дом «Вильямс», 2002. с. 251. — ISBN 5-8459-0261-4