Алгоритм Апостолико-Крочемора — различия между версиями
(→Псевдокод) |
(→Описание алгоритма) |
||
| Строка 21: | Строка 21: | ||
| − | Пусть теперь <tex>l = 0</tex>, если <tex>x = c ^ m</tex> и <tex>c \in \Sigma</tex>, иначе <tex>l</tex> равно позиции первого элемента, который не равен <tex>x[0]</tex> (<tex>x = a ^ l bu</tex>, где <tex>a \in \Sigma</tex>, <tex>b \in \Sigma</tex>, <tex>a \neq b</tex>, <tex>u \in \Sigma^*</tex>). | + | Пусть теперь <tex>l = 0</tex>, если <tex>x = c ^ m</tex> и <tex>c \in \Sigma</tex>, иначе <tex>l</tex> равно позиции первого элемента, который не равен <tex>x[0]</tex> (<tex>x = a ^ l bu</tex>, где <tex>a \in \Sigma</tex>, <tex>b \in \Sigma</tex>, <tex>a \neq b</tex>, <tex>u \in \Sigma^*</tex>). При каждой подстановке шаблона к тексту к позиции <tex>i</tex> мы проводим следующие сравнения: <tex>x[l] = y[i + l], x[l + 1] = y[i + l + 1], \ldots , x[m - 2] = y[i + m - 2], x[m - 1] = y[i + m - 1],</tex><tex> x[0] = y[i], x[1] = y [i + 1], \ldots , x[l - 1] = y[i + l - 1]</tex>. |
| + | |||
Во время поиска вхождений мы рассматриваем данную тройку <tex>(i, j, k)</tex> где: | Во время поиска вхождений мы рассматриваем данную тройку <tex>(i, j, k)</tex> где: | ||
Версия 21:26, 17 марта 2016
Алгоритм Апостолико — Крочемора (англ. Apostolico — Crochemore algorithm) — алгоритм поиска подстроки в строке.
Содержание
Описание алгоритма
Нам даны: — текст, — образец, , .
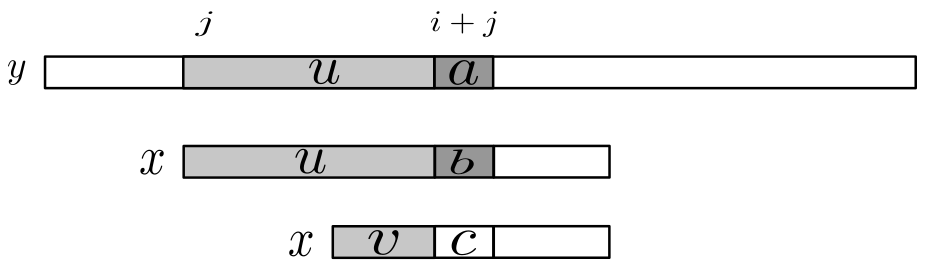
Для начала рассмотрим ситуацию, когда мы сравниваем наш образец с . Предположим, что при . Тогда и . Когда сдвиг возможен, разумно ожидать, что префикс шаблона совпадет c некоторым суффиксом . Более того, если мы хотим избежать несовпадения при сдвиге, то нужно, чтобы символ, следующий за префиксом в шаблоне, не совпадал с . Такой наибольший префикс называется помеченным бордером строки .
| Определение: |
| Помеченный бордер (англ. tagged border) строки — строка . |
Введем обозначение: пусть — длина наибольшего бордера для за которым следует символ и если нет такого помеченного бордера, где (). Затем, после сдвига, сравнение можно продолжить между символами и не потеряв никакого вхождения в и избежав отступа по тексту (смотри рисунок ниже).
Примечание: — помеченный бордер строки .
Пусть теперь , если и , иначе равно позиции первого элемента, который не равен (, где , , , ). При каждой подстановке шаблона к тексту к позиции мы проводим следующие сравнения: .
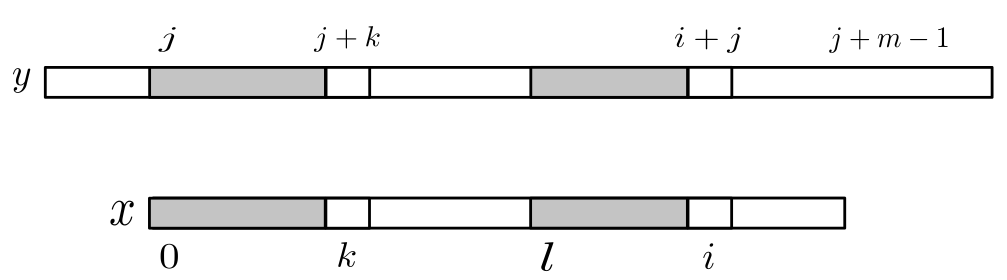
Во время поиска вхождений мы рассматриваем данную тройку где:
- шаблон сравнивается с
- и
- и
(см. рисунок ниже)
Вначале инициализируем эту тройку . Теперь опишем, как по уже вычисленной тройке перейти к следующей. Возможны три случая в зависимости от значения :
- :
- Если , тогда следующая тройка .
- Если , тогда следующая тройка .
-
- Если , тогда следующая тройка .
- Если , тогда возможны два случая в зависимости от значения :
- Если , тогда следующая тройка .
- Если , тогда следующая тройка .
- :
- Если и , тогда следующая тройка .
- Иначе либо и , либо . Если , то вхождение в найдено. В обоих случаях следующая тройка вычисляется, как в случае .
Псевдокод
void getT(string x, int t[]): //функция, вычисляющая массив для строки int i = 0 int j = t[0] = -1 while i < x.size while j > -1 and x[i] x[j] j = t[j] i++ j++ if x[i] == x[j] t[i] = t[j] else t[i] = j vector aG(string x, string y): // — образец, — текст int l int t[x.size] vector v //этап предпосчета getT(x, t) //вычисление значения for l = 1; x[l - 1] == x[l]; l++ if l == x.size l = 0 //этап поиска int i = l int j = 0 int k = 0 while j y.size - x.size while i < x.size and x[i] == y[i + j] // если ++i // тогда следующая тройка if i x.size while k < l and x[k] == y[j + k] // если и ++k // тогда следующая тройка if k l // если v.pushBack(j) // тогда найдена подстрока в позиции j j += i - t[i] // вычисляем новый сдвиг if i == l k = max(0, k - 1) // если и , тогда следующая тройка else if t[i] l // если , тогда следующая тройка k = max(0, t[i]) i = l else // если , тогда следующая тройка k = l i = t[i] return v
Пример
| Изображение | Описание | |
|---|---|---|
|
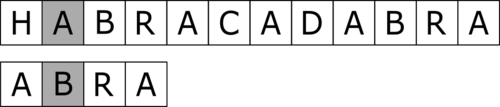
step 1 | |

|
step 2 | |
|
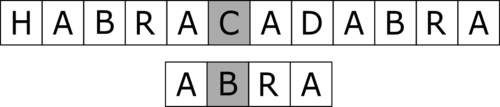
step 3 | |
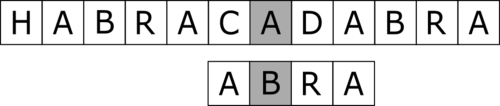
|
step 4 | |
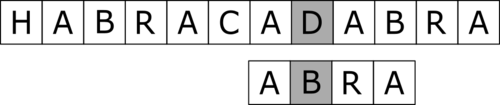
|
step 5 | |
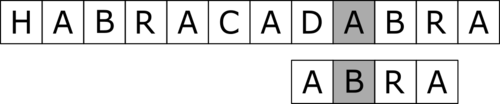
|
step 6 | |
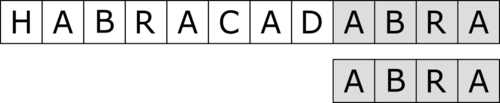
|
step 7 |
Асимптотика алгоритма
Этап предподсчета, а именно вычисление массива и переменной занимает времени и константное количество памяти. Этап поиска занимает времени, более того, алгоритм в худшем случае выполнит сравнений.