Алгоритм поиска подстроки в строке с помощью суффиксного массива

Далее будут рассмотрены некоторые способы нахождения всех вхождений образца в текст с помощью суффиксного массива.

Наивный алгоритм поиска

Простейший способ узнать, встречается ли образец в тексте, используя суффиксный массив, — взять первый символ образца и бинарным поиском по суффиксному массиву найти диапазон с суффиксами, начинающимися на такую же букву. Так как все элементы в полученном диапазоне отсортированы, а первые символы одинаковые, то оставшиеся после отбрасывания первого символа суффиксы тоже отсортированы. А значит, можно повторять процедуру сужения диапазона поиска уже по второму, затем третьему и так далее символу образца до получения либо пустого диапазона, либо успешного нахождения всех символов образца.

Бинарный поиск работает за время равное [math] O(\log|s|) [/math], а сравнение суффикса с образцом не может превышать длины образца.

Таким образом время работы алгоритмы [math] O(|p|\log|s|)[/math], где [math] s [/math] — текст, [math] p [/math] — образец.

Псевдокод

Поиск диапазона

[math] \mathtt {cmp (k)}[/math] — функция, сравнивающая строки по [math]k[/math]-тому символу.

[math] \mathtt {lower}[/math]_[math]\mathtt {bound (left, right, value, cmp)}[/math], [math] \mathtt {upper}[/math]_[math]\mathtt {bound (left, right, value, cmp)}[/math] — функции бинарного поиска.

Элементы строк нумеруются с единицы

function elementary_search():
    left = 0                                          // left, right — границы диапазона 
    right = n                                         //  n —  длина образца 
    for i = 1 to n 
        left = lower_bound(left, right, p[i], cmp (i) )
        right = upper_bound(left, right, p[i], cmp (i) )
    if (right - left > 0)   
        yield left                   
        yield right                 
    else
        yield "No matches";

Более быстрый поиск

Существует более быстрый алгоритм поиска образца в строке. Для этого используется [math]\mathtt {lcp} [/math] (longest common prefix).

Условные обозначения

• [math] L_p [/math] и [math] R_p [/math] — левая и правая границы диапазона ответов в суффиксном массиве [math] array [/math].
• [math] L [/math] — левая граница диапазона поиска (изначально равна [math]0[/math]).
• [math] R [/math] — правая граница диапазона поиска (изначально равна [math] |S| - 1 [/math]).
• [math] M = (L + R) / 2 [/math].
• [math] l = [/math][math]\mathtt {lcp(array[L], p)} [/math].
• [math] r = [/math][math]\mathtt {lcp(array[R], p)} [/math].
• [math] m_l = [/math][math]\mathtt {lcp(array[L], array[M])} [/math].
• [math] m_r = [/math][math]\mathtt {lcp(array[M], array[R])} [/math].

Алгоритм:

У любого суффикса в пределах диапазона от [math] L_p [/math] до [math] R_p [/math] есть префикс, который полностью совпадает с образцом.

В самом начале просто посчитаем [math] l [/math] и [math] r [/math] за линейное время, а во время выполнения алгоритма прямой пересчет производиться не будет, изменения будут происходить за [math] O(1) [/math].

Подсчет [math] m_l [/math] и [math] m_r [/math] можно производить за [math] O(1) [/math], если применять алгоритм Фарака-Колтона и Бендера. Любая пара суффиксов [math] array [/math] из диапазона [math] [L, M] [/math] имеет хотя бы [math] m_l [/math] совпадений в префиксах. Аналогично любая пара суффиксов [math] array [/math] из диапазона [math] [M, R] [/math] имеет хотя бы [math] m_r [/math] совпадений в префиксах.

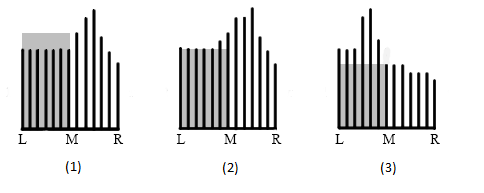
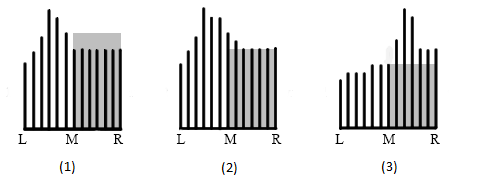
Рисунки:

• Черная вертикальная линия на рисунке обозначает [math]\mathtt {lcp} [/math] от [math] i [/math]-го суффикса суффиксного массива [math] array [/math] и образца [math] p [/math]. Чем линия длиннее, тем совпадений символов больше.
• [math] L [/math], [math] M [/math] и [math] R [/math] — то же самое, что в алгоритме. Кроме того, самая левая черная вертикальная линия на каждом рисунке означает [math] l [/math], аналогично, самая правая черная вертикальная линия на каждом рисунке означает [math] r [/math]. Переменная [math] m_l [/math] — это [math]\mathtt {lcp} [/math] в суффиксном массиве на промежутке [math] [L, M] [/math]. Переменная [math] m_r [/math] — это [math]\mathtt {lcp} [/math] в суффиксном массиве на промежутке [math] [M, R] [/math].
• Серым цветом выделен [math]\mathtt {lcp} [/math] в суффиксном массиве на рассматриваемом промежутке.

Поиск границ диапазона ответов

Рассмотрим поиск левой границы диапазона ответов [math] L_p [/math].

Сразу проверим образец с суффиксами по краям исходного диапазона поиска [math] L [/math] и [math] R [/math]: если образец лексикографически больше последнего суффикса [math] array [/math] или меньше первого суффикса, то образец не встречается в строке вовсе и поиск можно прекратить.

[math] L_p [/math] ищется при помощи бинарного поиска по суффиксному массиву [math] array [/math]. На каждом шаге поиска нам надо определять, на каком отрезке [math] [L, M] [/math] или [math] [M, R] [/math] надо продолжать поиск границы [math] L_p [/math]. Каждую итерацию бинарного поиска будем сравнивать [math] l [/math] и [math] r [/math]. Если [math] l \geqslant r [/math], то возможно одно из трех:

1. [math] m_l \gt l [/math]. Это означает, что каждая пара суффиксов из диапазона [math] [L, M] [/math] имеет между собой больше совпадений, чем суффикс с левого края с образцом, поэтому продолжим поиск в диапазоне [math] [M, R] [/math]. Значение [math] l [/math] при этом не меняется, а [math] L = M [/math].
2. [math] m_l = l [/math]. Это означает, что у каждого суффикса из [math] [L, M] [/math] есть хотя бы [math] l [/math] совпадений с образцом. Проверим суффикс в позиции [math] M [/math], так как с ним совпадений у образца может получиться больше. Начнем сравнивать суффикс в позиции [math] M [/math] начиная с [math] l [/math]-ого символа. Мы либо найдем полное вхождение образца в суффикс, либо на каком-то шаге [math] k [/math] получим несоответствие. В первом случае [math] R = M [/math] и [math] r = |p| [/math], так как мы ищем левую границу диапазона ответов. Во втором случае все зависит от лексикографического несовпадения. Если символ [math] l + k + 1 [/math] у образца меньше, чем у суффикса, то [math] R = M [/math] и [math] r = l + k + 1[/math], иначе [math] L = M [/math] и [math] l = l + k + 1[/math].
3. [math] m_l \lt l [/math]. Это означает, что совпадений у суффикса с левого края диапазона поиска с образцом больше, чем у суффикса в позиции [math] M [/math]. Очевидно, что поиск надо продолжать между [math] L [/math] и [math] M [/math], то есть [math] R = M [/math], а новое значение [math] r = m_l [/math].

Если [math] l \lt r [/math], то действия аналогичны. Также три случая:

1. [math] m_r \gt r [/math]. Сдвигаем [math] R [/math] в [math] M [/math]. Значение [math] r [/math] не изменяется.
2. [math] m_r = r [/math]. Считаем [math]\mathtt {lcp} [/math] для образца и суффикса, стоящего в позиции [math] M [/math], начиная с позиции [math] r [/math].
3. [math] m_r \lt r [/math]. Сдвигаем [math] L [/math] в [math] M [/math], [math] l = m_r [/math].

Бинарный поиск будет работать до тех пор, пока [math] R - L \gt 1 [/math]. После этого можно присвоить левой границе диапазона ответов [math] L_p = R [/math] и переходить к поиску правой границы диапазона ответов [math] R_p [/math].

Рассуждения при поиске [math] R_p [/math] аналогичны, только нужно не забыть изменить границы поиска на изначальные [math] L = 0 [/math] и [math] R = |s| - 1 [/math].

Таким образом часть бинарного поиска мы сделаем при сравнении нескольких [math]\mathtt {lcp} [/math] между собой(каждое за [math] O(1) [/math]), а если дойдет до сравнения символов, то любой символ [math] p [/math] сравнивается не более одного раза(при сравнении мы берем [math]\mathtt {max}[/math][math](l, r) [/math], а значит никогда не возвращаемся назад). В самом начале мы посчитали [math] l [/math] и [math] r [/math] за [math] O(p) [/math]. В итоге получаем сложность алгоритма [math] O(p + log(s)) [/math]. Правда нужен предподсчет, чтобы можно было брать [math]\mathtt {lcp} [/math] для двух любых суффиксов [math] array [/math] за [math] O(1) [/math], начиная с позиции [math] r [/math].

Псевдокод

Массивы и строки нумеруются с нуля.

Сравнения [math]\lt _z , \gt _z , =_z , \leqslant_z , \geqslant_z [/math] означают лексикографическое сравнение двух строк по их первым [math]z[/math] символам.

Сравнения [math]\lt , \gt , == , \leqslant , \geqslant [/math] при применении к строкам означают полное лексикографическое сравнение строк.

Функция [math]\mathtt {lcp}[/math]_[math]\mathtt{z(s, p)}[/math] ищет количество совпадений символов строк [math]s[/math] и [math]p[/math] начиная с позиции [math]z[/math].

[math]n[/math] — длина строки [math]s[/math], [math]w[/math] — длина строки [math]p[/math].

В алгоритме используются переменные, введенные выше в разделе "более быстрый поиск".

Поиск левой границы ответов [math] L_p [/math].

function find_L_p():
    l = lcp(p, s[array[0]])
    r = lcp(p, s[array[n - 1]])
    if (l == w or p < s[array[0]])
        L_p = 0 
    else if (p > s[array[n - 1])
        L_p = n
    else 
        L = 0
        R = n - 1
        while (R - L > 1) do 
            M = (L + R) / 2
            m_l = lcp(array[L], array[M])
            m_r = lcp(array[M], array[R])
            if (l [math]\geqslant[/math] r)
                if (m_l [math]\geqslant[/math] l)
                    m = l + lcp_l(s[array[M]], p)
                else
                    m = m_l
            else
                if (m_r [math]\geqslant[/math] r)
                    m = r + lcp_r(s[array[M]], p)
                else
                    m = m_r
            if (m == w || p [math]\leqslant[/math][math]_m[/math] s[array[M]]){
                R = M
                r = m
            else 
                L = M
                l = m
        L_p = R

См. также

• Алгоритм цифровой сортировки суффиксов циклической строки
• Алгоритм Касаи и др.
• Построение суффиксного массива с помощью стандартных методов сортировки

Источники информации

• Habrahabr — Суффиксный массив — удобная замена суффиксного дерева
• U. Manber and G. Mayers. — "Suffix arrays: A new method for on-line string searches"