Z-функция — различия между версиями
(→Построение Z-функции по префикс-функции) |
(→Построение Z-функции по префикс-функции) |
||
| Строка 119: | Строка 119: | ||
Таким образом, мы рассмотрели все случаи, при которых <tex>z[i] \ne 0</tex>, и показали корректность восстановления блока. | Таким образом, мы рассмотрели все случаи, при которых <tex>z[i] \ne 0</tex>, и показали корректность восстановления блока. | ||
==Построение Z-функции по префикс-функции== | ==Построение Z-функции по префикс-функции== | ||
| − | [[Файл:Case one.png|300px|thumb|right|Случай первый]] | + | [[Файл:Case one.png|300px|thumb|right|'''Случай первый''']] |
| − | [[Файл:Case two.png|300px|thumb|right|Случай второй]] | + | [[Файл:Case two.png|300px|thumb|right|'''Случай второй''']] |
| − | [[Файл:Case three.png|300px|thumb|right|Случай третий]] | + | [[Файл:Case three.png|300px|thumb|right|'''Случай третий''']] |
=== Постановка задачи === | === Постановка задачи === | ||
Дан массив с корректной [[Префикс-функция | префикс-функцией]] для строки <tex>s</tex>, получить за <tex>O(n)</tex> массив с Z-функцией для строки <tex>s</tex>. | Дан массив с корректной [[Префикс-функция | префикс-функцией]] для строки <tex>s</tex>, получить за <tex>O(n)</tex> массив с Z-функцией для строки <tex>s</tex>. | ||
Версия 19:28, 7 апреля 2016
| Определение: |
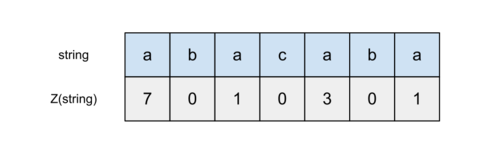
| Z-функция (англ. Z-function) от строки и позиции — это длина максимального префикса подстроки, начинающейся с позиции в строке , который одновременно является и префиксом всей строки . Более формально, . Значение Z-функции от первой позиции не определено, поэтому его обычно приравнивают к нулю или к длине строки. |
Примечание: далее в конспекте символы строки нумеруются с нуля.
Содержание
Тривиальный алгоритм
Простая реализация за , где — длина строки. Для каждой позиции перебираем для неё ответ, начиная с нуля, пока не обнаружим несовпадение или не дойдем до конца строки.
Псевдокод
int[] zFunction(s : string):
int[] zf = int[n]
for i = 1 to n − 1
while i + zf[i] < n and s[zf[i]] == s[i + zf[i]]
zf[i]++
return zf
Эффективный алгоритм поиска
Z-блоком назовем подстроку с началом в позиции и длиной .
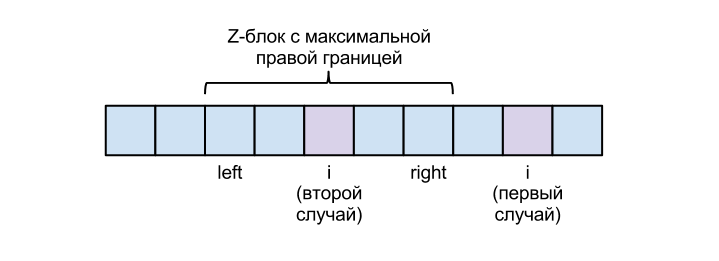
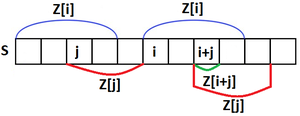
Для работы алгоритма заведём две переменные: и — начало и конец Z-блока строки с максимальной позицией конца (среди всех таких Z-блоков, если их несколько, выбирается наибольший). Изначально и .
Пусть нам известны значения Z-функции от до . Найдём .
Рассмотрим два случая.
- :
Просто пробегаемся по строке и сравниваем символы на позициях и .Пусть первая позиция в строке для которой не выполняется равенство , тогда это и Z-функция для позиции . Тогда . В данном случае будет определено корректное значение в силу того, что оно определяется наивно, путем сравнения с начальными символами строки. - :
Сравним и . Если меньше, то надо просто наивно пробежаться по строке начиная с позиции и вычислить значение . Корректность в таком случае также гарантирована.Иначе мы уже знаем верное значение , так как оно равно значению .
Время работы
Этот алгоритм работает за , так как каждая позиция пробегается не более двух раз: при попадании в диапазон от до и при высчитывании Z-функции простым циклом.
Псевдокод
int[] zFunction(s : string):
int[] zf = int[n]
int left = 0, right = 0
for i = 1 to n − 1
zf[i] = max(0, min(right − i, zf[i − left]))
while i + zf[i] < n and s[zf[i]] == s[i + zf[i]]
zf[i]++
if i + zf[i] >= right
left = i
right = i + zf[i]
return zf
Поиск подстроки в строке с помощью Z-функции
— длина текста. — длина образца.
Образуем строку s = pattern + # + text, где # — символ, не встречающийся ни в text, ни в pattern. Вычисляем Z-функцию от этой строки.
В полученном массиве, в позициях в которых значение Z-функции равно , по определению начинается подстрока, совпадающая с pattern.
Псевдокод
int substringSearch(text : string, pattern : string):
int[] zf = zFunction(pattern + '#' + text)
for i = m + 1 to n + 1
if zf[i] == m
return i
Построение строки по Z-функции
| Задача: |
| Восстановить строку по Z-функции за , считая алфавит ограниченным. |
Описание алгоритма
Пусть в массиве хранятся значения Z-функции, в будет записан ответ. Пойдем по массиву слева направо.
Нужно узнать значение . Для этого посмотрим на значение : если , тогда в запишем ещё не использованный символ или последний использованный символ алфавита, если мы уже использовали все символы. Если , то нам нужно записать префикс длины строки . Но если при посимвольном записывании этого префикса в конец строки мы нашли такой (индекс последнего символа строки), что больше, чем длина оставшейся незаписанной части префикса, то мы перестаём писать этот префикс и пишем префикс длиной строки .
Для правильной работы алгоритма, будем считать значение равным нулю.
Алгоритм всегда сможет построить строку по корректному массиву значений Z-функции, если в алфавите больше одного символа.
Реализация
string buildFromZ(z : int[], alphabet : char[]):
string s = ""
int prefixLength = 0 // длина префикса, который мы записываем
int j // позиция символа в строке, который будем записывать
int newCharacter = 0 // индекс нового символа
for i = 0 to z.length - 1
// мы не пишем какой-то префикс и не будем писать новый
if z[i] = 0 and prefixLength = 0
if newCharacter < alphabet.length
s += alphabet[newCharacter]
newCharacter++
else
s += alphabet[newCharacter - 1]
// нам нужно запомнить, что мы пишем префикс
if z[i] > prefixLength
prefixLength = z[i]
j = 0
// пишем префикс
if prefixLength > 0
s += s[j]
j++
prefixLength--
return s
Доказательство корректности алгоритма
Докажем, что если нам дали корректную Z-функцию, то наш алгоритм построит строку с такой же Z-функцией.
Пусть — данная Z-функция, строку построил наш алгоритм, — массив значений Z-функции для .
Если , то и , так как (в результате алгоритма мы получаем, что , а ).
Рассмотрим значения . В этом случае является началом префикса исходной строки. Назовём подстроку, совпадающую с некоторым префиксом строки, блоком. Возможны три положения блока, относительно других блоков.
- Он не пересекает другие блоки (но может полностью включать в себя какой-то блок). Тогда , потому что наш алгоритм полностью скопирует префикс всей строки.
- Рассмотрим случай, когда мы записали часть префикса и прервались для написания нового. Новый блок корректно закончит предыдущий блок (иначе бы массив был бы некорректен, и предыдущий блок будет совпадать с префиксом, тогда .
- Если блок лежит внутри другого блока, то его массив совпадает с массивом для блока, содержащегося в префиксе строки. Проверяем корректность массива для этого блока.
Таким образом, мы рассмотрели все случаи, при которых , и показали корректность восстановления блока.
Построение Z-функции по префикс-функции
Постановка задачи
Дан массив с корректной префикс-функцией для строки , получить за массив с Z-функцией для строки .
Описание алгоритма
Пусть префикс функция хранится в массиве . Z-функцию будем записывать в массив . Заметим, что если , то мы можем заявить, что будет не меньше, чем .
Так же заметим, что после такого прохода в будет максимальное возможное значение. Далее будем поддерживать инвариант: в будет максимальное возможное значение.
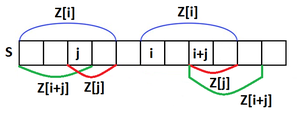
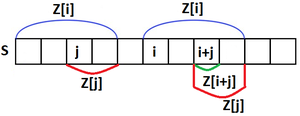
Пусть в , рассмотрю , и . Заметим, что совпадает с и тогда возможны три случая:
- . Тогда мы не можем увеличить значение и надо рассматривать уже .
- и . Тогда очевидно, что можно увеличить до .
- и . Тогда понятно, что .
Псевдокод
int[] buildZFunctionFromPrefixFunction(int[] P)
int n = P.length;
int[] Z = new int[n]
for(int i = 1; i < n; i++)
if(P[i])
Z[i - P[i] + 1] = P[i]
Z[0] = n;
int t
for(int i = 1; i < n - 1; i++)
t = i;
if(Z[i])
for(int j = 1; j < Z[i] && Z[i + j] <= Z[j]; j++)
Z[i + j] = min(Z[j], Z[i] - j)
t = i + j
i = t
return Z