Коды Грея для перестановок — различия между версиями
Niko (обсуждение | вклад) |
Niko (обсуждение | вклад) |
||
| Строка 84: | Строка 84: | ||
== См. также == | == См. также == | ||
* [[Коды Грея]] | * [[Коды Грея]] | ||
| − | * [[ | + | * [[Комбинаторные объекты]] |
| + | * [[Гамильтонов путь]] | ||
Версия 09:58, 3 декабря 2010
код Грея для перестановки при n = 2
1 2 2 1 |
код Грея для перестановки при n = 3
1 2 3 2 1 3 2 3 1 3 2 1 3 1 2 1 3 2 |
код Грея для перестановки при n = 4
1 2 3 4 2 1 3 4 2 3 1 4 2 3 4 1 3 2 4 1 3 2 1 4 3 1 2 4 1 3 2 4 1 3 4 2 3 1 4 2 3 4 1 2 3 4 2 1 4 3 2 1 4 3 1 2 4 1 3 2 1 4 3 2 1 4 2 3 4 1 2 3 4 2 1 3 4 2 3 1 2 4 3 1 2 4 1 3 2 1 4 3 1 2 4 3 |
Содержание
Определение
Коды Грея для перестановок - называют такое упорядочение перестановок, что соседние перестановки отличаются только элементарной транспозицией.
Построения Кода Грея для перестановок на Pascal
for i := 1 to n do
begin
P[i] := i; //перестановка
C[i] := 1; //показывает, какую из возможных n - i + 1 позиций i занимает относительно элементов i + 1, .., n
PR[i] := true; //содержит информацию о том, переносился ли элемент i вперед или назад
end;
C[n] := 0;
for g := 1 to n - 1 do
write(P[g], ' ');
writeln(P[n]);
i := 1;
while i < n do
begin
i := 1;
x := 0;
while C[i] = n - i + 1 do
begin
PR[i] := not PR[i];
C[i] := 1;
if PR[i] then x := x + 1;
i := i + 1;
end;
if i < n then
begin
if PR[i] then k := C[i] + x
else k := n - i + 1 - C[i] + x;
swap(P[k], P[k + 1]); // меняем местами значения P[k] и P[k + 1]
for g := 1 to n - 1 do
write(P[g], ' ');
writeln(P[n]);
C[i] := C[i] + 1
end;
end;
Сведение задачи построение кода Грея для перестановок к графам
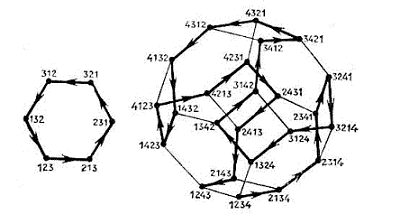
Последовательность перестановок, полученная с помощью данного алгоритма имеет интересную интерпретацию. Так, если рассмотреть граф, вешины которого соответствуют всем перестановкам и в котором две вершины, соответствующие перестановкам f и g, соединены ребром, если g образуется из f однократной транспозицией соседних элементов, то полученная последовательность является гамильтоновым путем в этом графе. На рисунке изображен граф последовательности для n = 3, 4.