Арифметическое кодирование — различия между версиями
Migan (обсуждение | вклад) м (→Псевдокод) |
Migan (обсуждение | вклад) |
||
| Строка 13: | Строка 13: | ||
=== Псевдокод === | === Псевдокод === | ||
| − | <tex>s</tex> {{---}} текст, подаваемый на вход | + | *<tex>s</tex> {{---}} текст, подаваемый на вход |
| + | *<tex>left</tex>, <tex>right</tex> {{---}} границы отрезка, содержащего возможный результат арифметического кодирования | ||
| + | *<tex>segment</tex> {{---}} структура, задающая подотрезок отрезка <tex>[0; 1)</tex>, соответствующего конкретному символу на основе частотного анализа. Имеет поля: | ||
| + | ** <tex>left</tex> {{---}} левая граница подотрезка | ||
| + | ** <tex>right</tex> {{---}} правая граница подотрезка | ||
| − | + | '''double''' ArithmeticCoding(s: '''string'''): | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''double''' ArithmeticCoding (s: '''string'''): | ||
left = 0 | left = 0 | ||
right = 1 | right = 1 | ||
| Строка 40: | Строка 38: | ||
=== Псевдокод === | === Псевдокод === | ||
| − | <tex>code</tex> {{---}} вещественное число, подаваемое на вход | + | *<tex>code</tex> {{---}} вещественное число, подаваемое на вход |
| − | + | *<tex>length</tex> {{---}} длина восстанавливаемого текста | |
| − | <tex>length</tex> {{---}} длина восстанавливаемого текста | + | *<tex>segment</tex> {{---}} структура, задающая подотрезок отрезка <tex>[0; 1)</tex>, соответствующего конкретному символу на основе частотного анализа. Имеет поля: |
| − | + | ** <tex>left</tex> {{---}} левая граница подотрезка | |
| − | <tex>segment</tex> {{---}} структура, задающая подотрезок отрезка <tex>[0; 1)</tex>, соответствующего конкретному символу на основе частотного анализа. Имеет поля: | + | ** <tex>right</tex> {{---}} правая граница подотрезка |
| − | * <tex>left</tex> {{---}} левая граница подотрезка | + | ** <tex>character</tex> {{---}} значение символа |
| − | * <tex>right</tex> {{---}} правая граница подотрезка | ||
| − | * <tex>character</tex> {{---}} значение символа | ||
<code> | <code> | ||
| − | '''string''' ArithmeticDecoding (code: '''double'''): | + | '''string''' ArithmeticDecoding(code: '''double'''): |
s = "" | s = "" | ||
'''for''' i = 1 '''to''' length | '''for''' i = 1 '''to''' length | ||
| Строка 66: | Строка 62: | ||
== Пример работы == | == Пример работы == | ||
| − | Рассмотрим в качестве примера строку <tex>abacaba</tex> | + | Рассмотрим в качестве примера строку <tex>abacaba</tex>: |
=== Кодирование === | === Кодирование === | ||
{|class="wikitable" | {|class="wikitable" | ||
| Строка 147: | Строка 143: | ||
| − | ||proof= | + | ||proof=Введём следующие обозначения: |
| + | <tex>l</tex> {{---}} длина текста; | ||
| + | <tex>n</tex> {{---}} размер алфавита; | ||
| + | <tex>f_i</tex> {{---}} частота встречаемости символа; | ||
| + | <tex>p_i</tex> {{---}} вероятность вхождения символа; | ||
| + | |||
| + | Размер сообщения <tex>L</tex> можно найти по формуле: <tex> L = \prod\limits_{i=1}^l p_{fi} = \prod\limits_{i=1}^n p_{i}^{f_{i}}</tex> | ||
Число бит в закодированном тексте: <tex>\log_2 L = \sum\limits_{i=1}^n f_i\cdot \log_2 p_i = l \cdot \sum\limits_{i=1}^n p_i\cdot \log_2 p_i = -l \cdot H(p_1...p_n)</tex> | Число бит в закодированном тексте: <tex>\log_2 L = \sum\limits_{i=1}^n f_i\cdot \log_2 p_i = l \cdot \sum\limits_{i=1}^n p_i\cdot \log_2 p_i = -l \cdot H(p_1...p_n)</tex> | ||
Версия 17:36, 17 июня 2016
Арифметическое кодирование (англ. Arithmetic coding) — алгоритм сжатия информации без потерь, который при кодировании ставит в соответствие тексту вещественное число из отрезка . Данный метод, как и алгоритм Хаффмана, является энтропийным, т.е. длина кода конкретного символа зависит от частоты встречаемости этого символа в тексте. Арифметическое кодирование показывает более высокие результаты сжатия, чем алгоритм Хаффмана, для данных с неравномерными распределениями вероятностей кодируемых символов. Кроме того, при арифметическом кодировании каждый символ кодируется нецелым числом бит, что эффективнее кода Хаффмана (теоретически, символу с вероятностью появления допустимо ставить в соответствие код длины , следовательно, при кодировании алгоритмом Хаффмана это достигается только с вероятностями, равными обратным степеням двойки).
Содержание
Принцип действия
Кодирование
На вход алгоритму передаются текст для кодирования и список частот встречаемости символов.
- Рассмотрим отрезок на координатной прямой.
- Поставим каждому символу текста в соответствие отрезок, длина которого равна частоте его появления.
- Считаем символ из входного потока и рассмотрим отрезок, соответствующий этому символу. Разделим этот отрезок на части, пропорциональные частотам встречаемости символов.
- Повторим пункт (3) до конца входного потока.
- Выберем любое число из получившегося отрезка, которое и будет результатом арифметического кодирования.
Псевдокод
- — текст, подаваемый на вход
- , — границы отрезка, содержащего возможный результат арифметического кодирования
- — структура, задающая подотрезок отрезка , соответствующего конкретному символу на основе частотного анализа. Имеет поля:
- — левая граница подотрезка
- — правая граница подотрезка
double ArithmeticCoding(s: string):
left = 0
right = 1
for i = 0 to length(s)-1
symb = s[i]
newRight = left + (right - left) * segment[symb].right
newLeft = left + (right - left) * segment[symb].left
left = newLeft
right = newRight
return (left + right) / 2
Декодирование
Алгоритм по вещественному числу восстанавливает исходный текст.
- Выберем на отрезке , разделенном на части, длины которых равны вероятностям появления символов в тексте, подотрезок, содержащий входное вещественное число. Символ, соответствующий этому подотрезку, дописываем в ответ.
- Нормируем подотрезок и вещественное число.
- Повторим пункты 1—2 до тех пор, пока не получим ответ.
Псевдокод
- — вещественное число, подаваемое на вход
- — длина восстанавливаемого текста
- — структура, задающая подотрезок отрезка , соответствующего конкретному символу на основе частотного анализа. Имеет поля:
- — левая граница подотрезка
- — правая граница подотрезка
- — значение символа
string ArithmeticDecoding(code: double):
s = ""
for i = 1 to length
for j = 1 to n
if code >= segment[j].left and code < segment[j].right
s = s + segment[j].character
code = (code – segment[j].left) / (segment[j].right – segment[j].left)
break
return s
Замечание: кодировщику и декодировщику должно быть известно, когда завершать работу. Для этого можно передавать в качестве аргумента длину текста или символ конца файла, после которого процесс должен быть остановлен.
Для оптимизации размера кода необходимо выбрать из окончательного диапазона число, содержащее наименьшее количество знаков в двоичной записи.
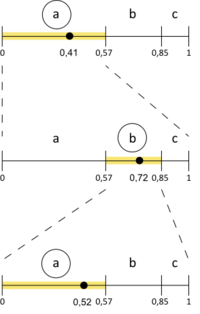
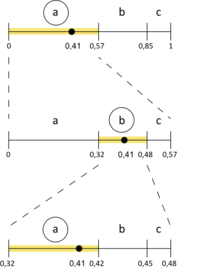
Пример работы
Рассмотрим в качестве примера строку :
Кодирование
| Символ | Частота появления |
|---|---|
| |
| |
|
| Считанный символ | Левая граница отрезка | Правая граница отрезка |
|---|---|---|
| ||
| ||
| ||
| ||
| ||
| ||
| ||
|
Код:
Декодирование
Код:
| Декодируемый символ | Код |
|---|---|
| |
| |
| |
| |
| |
| |
|
Замечание: при декодировании текста можно не только нормализовывать рабочий отрезок и текущий код, но и уменьшать рабочий отрезок (аналогично кодированию), не изменяя значение кода.
Декодирование (второй способ)
Код:
| Декодируемый символ | Границы отрезка | |||
|---|---|---|---|---|
| ||||
| ||||
| ||||
| ||||
| ||||
| ||||
| ||||
Оценка длины кодового слова
| Теорема: |
При арифметическом кодировании длина кодового слова не превышает энтропии исходного текста. |
| Доказательство: |
|
Введём следующие обозначения: — длина текста; — размер алфавита; — частота встречаемости символа; — вероятность вхождения символа; Размер сообщения можно найти по формуле: Число бит в закодированном тексте: |