Детерминированные конечные автоматы

Определение:

Детерминированный конечный автомат (ДКА) (англ. deterministic finite automaton (DFA)) — набор из пяти элементов [math]\langle \Sigma , Q, s \in Q, T \subset Q, \delta : Q \times \Sigma \to Q \rangle[/math], где [math]\Sigma[/math] — алфавит (англ. alphabet), [math]Q[/math] — множество состояний (англ. finite set of states), [math]s[/math] — начальное (стартовое) состояние (англ. start state), [math]T[/math] — множество допускающих состояний (англ. set of accept states), [math]\delta[/math] — функция переходов (англ. transition function).

Процесс допуска

Изначально автомат находится в стартовом состоянии [math]s[/math]. Автомат считывает символы по очереди. При считывании очередного символа [math]p_i[/math] автомат переходит в состояние [math]\delta(q, p_i)[/math], где [math]q[/math] — текущее состояние автомата. Процесс продолжается до тех пор, пока не будет достигнут конец входного слова.

Определение:

Будем говорить, что автомат допускает (англ. accept) слово, если после окончания описанного выше процесса автомат окажется в допускающем состоянии.

Замечание. Если в какой-то момент из текущего состояния нет перехода по считанному символу, то будем считать, что автомат не допускает данное слово. При реализации вместо отдельного рассмотрения данного случая иногда удобно вводить фиктивную нетерминальную «дьявольскую вершину» (также тупиковое состояние, сток), из которой любой переход ведет в неё же саму, и заменить все несуществующие переходы на переходы в «дьявольскую вершину».

Способы представления

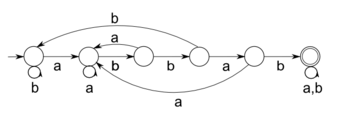
Диаграмма переходов

Диаграмма переходов — граф, вершины которого соответствуют состояниям автомата, а рёбра — переходам между состояниями.

[math]\bigcirc[/math] — нетерминальное состояние,

[math]\circledcirc[/math] — терминальное состояние,

Стрелка [math]\downarrow[/math] указывает на начальное состояние.

Пример	Описание
	Автомат для поиска образца в тексте для строки [math]abbab[/math].
	Автомат, принимающий непустые строки из чередующихся символов [math]a[/math] и [math]b[/math],без «дьявольской вершины».
	Автомат, принимающий непустые строки из чередующихся символов [math]a[/math] и [math]b[/math], с «дьявольской вершиной».

Таблица переходов

Таблица переходов [math]T (|Q| \times |\Sigma|)[/math], дающая табличное представление функции [math]\delta[/math].

[math]M = (Q, \Sigma , \delta, q_0, F)[/math], где

• [math]Q = {S_1, S_2}[/math],
• [math]\Sigma = \{0, 1 \}[/math],
• [math]q_0 = S_1[/math],
• [math]F = {S_1}[/math],
• [math]\delta[/math] — функция переходов, представленная таблицей:

	[math]0[/math]	[math]1[/math]
[math]S_1[/math]	[math]S_2[/math]	[math]S_1[/math]
[math]S_2[/math]	[math]S_1[/math]	[math]S_2[/math]

Автоматные языки

Определение:

Мгновенное описание (конфигурация) (англ. snapshot) — пара [math]\langle q, \alpha \rangle[/math], где [math]q[/math] — текущее состояние, [math]\alpha[/math] — оставшиеся символы.

Будем говорить, что конфигурация [math]\langle p, \beta \rangle[/math] выводима из [math]\langle q, \alpha \rangle[/math] за один шаг [math](\langle q, \alpha \rangle \vdash \langle p, \beta \rangle)[/math], если:

• [math]\alpha = c\beta[/math],
• [math]\delta (q, c)=p [/math].

Будем говорить, что конфигурация [math]\langle p, \beta \rangle[/math] выводима из [math]\langle q, \alpha \rangle[/math] за конечное число шагов [math](\langle q, \alpha \rangle \vdash^* \langle p, \beta \rangle)[/math], если [math]\exists n:[/math]

• [math]\alpha = c_1 c_2 ... c_n\beta[/math],
• [math]\langle q, c_1 c_2 c_3 ... c_n\beta \rangle \vdash \langle u_1, c_2 c_3 ... c_n\beta \rangle \vdash \langle u_2, c_3 ... c_n\beta \rangle \vdash ... \vdash \langle u_{n-1}, c_n\beta \rangle \vdash \langle p, \beta \rangle[/math].

Лемма:

[math]\langle q, \alpha \rangle \vdash^* \langle p, \varepsilon \rangle, \langle p, \beta \rangle \vdash^* \langle r, \varepsilon \rangle \Rightarrow \langle q, \alpha\beta \rangle \vdash^* \langle r, \varepsilon \rangle[/math].

Доказательство:

[math]\triangleright[/math]

[math]\langle q, \alpha\beta \rangle \vdash^* \langle p, \beta \rangle \vdash^* \langle r, \varepsilon \rangle.[/math]

[math]\triangleleft[/math]

Определение:

Множество [math]L(\mathcal{A})=\{\alpha \mid \exists t \in T : \langle s, \alpha \rangle \vdash^* \langle t, \varepsilon \rangle\}[/math] называется языком автомата (англ. automata's language) [math]\mathcal{A}[/math].

Иначе говоря, языком автомата является множество всех допускаемых им слов. Произвольный язык является автоматным, если существует ДКА, допускающий те и только те слова, которые принадлежат языку.

Определение:

Множество языков всех ДКА образует множество автоматных языков [math]\mathrm{AUT}[/math].

Изоморфизм двух автоматов

Определение:

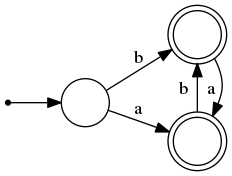
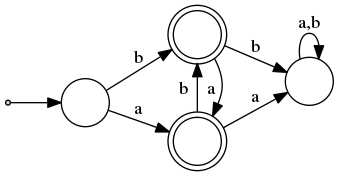
Автоматы называются изоморфными (англ. isomorphic), если существует биекция между их вершинами такая, что сохраняются все переходы, терминальные состояния соответствуют терминальным, начальные — начальным

Задача:

Задано два детерминированных конечных автомата. Определить, изоморфны ли они друг другу. Гарантируется, что все состояния автоматов достижимы.

Алгоритм

Из определения следует, что если автоматы изоморфны, то можно их состояния занумеровать одним способом так, что вершины из разных автоматов с одинаковыми номерами будут равны — то есть в каждом из этих двух состояний существует переход в какое-то состояние с таким же номером, что и переход по этой же букве в другом состоянии. Поэтому мы можем зафиксировать какую-то нумерацию, например, в порядке обхода в глубину по символам в лексикографическом порядке и просто проверить состояния с одинаковыми номерами на равенство. Если все состояния будут равны, то автоматы будут равны, в нашем случае будет следовать изоморфизм двух автоматов. Асимптотика алгоритма совпадает с асимптотикой обхода в глубину, то есть [math]O(N + M) [/math], где [math] N[/math] — суммарное число вершин в автоматах, [math] M[/math] — суммарное число ребер.

Псевдокод

• [math] \mathtt {Transitions} [/math] — множество пар [math]\langle a[/math], [math]T \rangle[/math] , где [math] a \in \Sigma[/math], [math]T \in Q[/math]

boolean dfs(u: Vertex, v: Vertex): 
   visited[u] = true   // заметим, что достаточно только одного массива [math]\mathtt{visited}[/math] на два автомата
   if (v.terminal != u.terminal)
     return false   
     
   boolean result = true
   for ([math]\langle c, q \rangle[/math] : u.transitions)      
     Vertex t1 = u.transitions.getVertex(c)
     Vertex t2 = v.transitions.getVertex(c)
     if одна из вершин t1, t2 дьявольская, а другая — нет
       return false
     if (not visited[t1]) 
       result = result and dfs(t1, t2)                
         
   return result

См. также

• Недетерминированные конечные автоматы
• Автомат для поиска образца в тексте
• Алгоритм Ахо-Корасик
• Теорема Клини (совпадение классов автоматных и регулярных языков)

Источники информации

• Хопкрофт Д., Мотвани Р., Ульман Д. Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. — М.:Издательский дом «Вильямс», 2002. — С. 61.— ISBN 5-8459-0261-4
• Lawson, Mark V. (2004). Finite automata. Chapman and Hall/CRC. ISBN 1-58488-255-7.
• Wikipedia — Deterministic finite automaton