Алгоритм Дейкстры

В ориентированном взвешанном графе [math]G = (V, E)[/math], вес рёбер которого неотрицателен и определяется весовой функцией [math]w(uv) \geqslant 0[/math], Алгоритм Дейкстры находит длину кратчайшего пути из одной вершины [math]s[/math] до всех остальных.

Алгоритм

В алгоритме поддерживается множество вершин [math]S[/math], для которых уже вычислены кратчайшие пути к ним из вершины [math]s[/math]. На каждой итерации основного цикла выбирается вершина [math] u \in V \setminus S[/math], которой на текущий момент соответствует минимальная оценка кратчайшего пути. Вершина [math]u[/math] добавляется в множество [math]S[/math] и производится релаксация всех исходящих из неё рёбер.

Псевдокод

Dijkstra([math]G[/math], [math]w[/math], [math]s[/math])
  [math]d \gets \infty[/math]
  [math]d[s] \gets 0[/math]
  [math]S \gets \emptyset[/math]
  while [math]V \setminus S \neq \emptyset[/math]
      do argmin([math]v : v \in V \setminus S, d[v][/math])
         [math]S \gets S \cup \{u\}[/math]
         for [math](uv) \in E[/math]
             do relax([math]u[/math], [math]v[/math], [math]w[/math])

Обоснование корректности работы

Теорема:

После окончания работы алгоритма Дейкстры для всех вершин [math]u \in V[/math] будет выполняться равенство [math]d[u] = \delta(s, u)[/math]

Доказательство:

[math]\triangleright[/math]

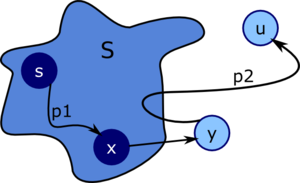
Рассмотрим инвариант основного цикла: в начале каждой итерации для всех вершин [math]v \in S[/math] выполняется [math]d[v] = \delta(s, v)[/math] Инициализация. Изначально множество [math]S[/math] пусто, инвариант выполняется. Рис. 1 Сохранение. Покажем, что при каждой итерации инвариант сохраняется для каждой вершины, добавленной в [math]S[/math], для этого воспользуемся методом «от противного». Предположим, что [math]u[/math] первая добавленная в [math]S[/math] вершина, для которой равенство [math]d[u] = \delta(s, u)[/math] не выполняется. Рассмотрим ситуацию, сложившуюся в начале итерации, в которой [math]u[/math] будет добавлена в [math]S[/math]. Рассмотрев кратчайший путь из [math]s[/math] в [math]u[/math], можно получить противоречие, заключающееся в том, что на рассматриваемый момент справедливо равенство [math]d[u] = \delta(s, u)[/math]. Должно выполняться условие [math]u \neq s[/math], так как [math]s[/math] является первой вершиной, добавленной в [math]S[/math] и в момент её добавления равенство [math]d[u] = \delta(s, u)[/math] выполняется. Из условия [math]u \neq s[/math] следует, в частности, что [math]S[/math] не пусто. Из вершины [math]s[/math] в вершину [math]u[/math] должен существовать какой-нибудь путь, так как иначе выполняется соотношение [math]d[u] = \delta(s, u) = \infty[/math], нарушающее предположение о том, что равенство [math]d[u] = \delta(s, u)[/math] не выполняется. Из существования пути следует, что существует и кратчайший путь [math]p[/math] из [math]s[/math] в [math]u[/math]. Перед добавлением [math]u[/math] в [math]S[/math] путь [math]p[/math] соединяет вершину из множества [math]S[/math] с вершиной принадлежащей множеству [math]V \setminus S[/math]. Рассмотрим первую вершину [math]y[/math] на пути [math]p[/math] принадлежащую [math]V \setminus S[/math], и положим, что её предшествует вершина [math]x \in S[/math]. Тогда, как видно из рис.1, путь [math]p[/math] можно разложить на составляющие [math]s \overset{p_1}{\leadsto} x \to y \overset{p_2}{\leadsto} u[/math]. Утверждается, что в момент добавления вершины [math]u[/math] в множество [math]S[/math], выполняется равенство [math]d[u] = \delta(s, y)[/math]. Так как вершина [math]u[/math] выбрана как первая вершина, после добавления которой в множество [math]S[/math] не выполянется соотношение [math]d[u] = \delta(s, u)[/math], то после добавления вершины [math]x[/math] в [math]S[/math] справедливо равенство [math]d[x] = \delta(s, x)[/math]. В это время происходит релаксация ребра [math]xy[/math]. В это время происходит релаксация ребра [math]xy[/math], поэтому вышеописанное утверждение выполняется. Поскольку на кратчайшем пути из [math]s[/math] в [math]u[/math] вершина [math]y[/math] находиться перед [math]u[/math] и вес каждого из ребер выражается неотрицательным значением, выполняется неравенство [math]\delta(s, y) \leqslant \delta(s, u)[/math], поэтому [math]d[y] = \delta(s, y) \leqslant \delta(s, u) \leqslant d[u][/math]. Но так как и вершина [math]u[/math], и вершина [math]y[/math] во время выбора вершины [math]u[/math] находились в множестве [math]V \setminus S[/math], выполняется неравенство [math]d[u] \leqslant d[y][/math]. Таким образом, оба [math]d[y] = \delta(s, y) = \delta(s, u) = d[u][/math]. Значит, [math]d[u] = \delta(s, u)[/math], что противоречит нашему выбору вершины [math]u[/math]. Следовательно, во время добавления вершины [math]u[/math] в множество [math]S[/math] выполняется равенство[math]d[u] = \delta(s, u)[/math], а следовательно, оно выполняется и в дальнейшем. Завершение. По завершении работы алгоритма множество [math]V \setminus S[/math] пусто. Из этого равенства следует, что [math]S = V[/math]. Таким образом, для всех вершин [math]u \in V[/math] выполняется равенство [math]d[u] = \delta(s, u)[/math].

[math]\triangleleft[/math]

Оценка сложности

Основной цикл выполняется [math]V[/math] раз. Релаксация выполниться всего [math]E[/math] раз. В реализации алгоритма присутствует функция argmin, ассимптотика её работы зависит от реализации.

Таким образом:

Структура данных для хранения множества [math]V \setminus S[/math]	Ассимптотика времени работы
Наивная реализация	[math]O(V^2+E)[/math]
Куча	[math]O(E\log{V})[/math]
Куча Фибоначчи	[math]O(V\log{V}+E)[/math]

Литература

• Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн Клиффорд Алгоритмы: построение и анализ, 2-е издание. Пер. с англ. — М.:Издательский дом "Вильямс", 2010. — 1296 с.: ил. — Парал. тит. англ. — ISBN 978-5-8459-0857-5 (рус.)