Участник:Dominica — различия между версиями
Dominica (обсуждение | вклад) м |
Dominica (обсуждение | вклад) м |
||
| Строка 1: | Строка 1: | ||
<tex dpi = "200" >1 \mid\mid \sum w_i U_i</tex> | <tex dpi = "200" >1 \mid\mid \sum w_i U_i</tex> | ||
| + | {{Утверждение | ||
| + | |id=krit_dol3 | ||
| + | |statement= | ||
| + | Критерии Делоне для ребер и треугольников равносильны. | ||
| + | |proof= | ||
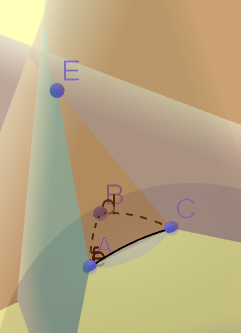
| + | [[Файл:dol3.png|400px|thumb|right|]] | ||
| + | Из треугольника в ребра: если для каждого треугольника выполнен критерий, то для каждого ребра можно рассматривать плоскость при любом треугольнике при ребре. | ||
| + | Обратно: Рассмотрим треугольник <tex>ABC</tex>, для каждого из ребра можно провести плоскость и они образуют трехмерный угол, снаружи которого нет точек. В пересечении угла и плосокости <tex>ABC</tex> образуется тетраэдр. Если в нем есть точки, то точки есть внутри треугольника, тогда это не триангуляция <tex>\implies</tex> точек в тетраэдре нет <tex>\implies</tex> плоскостью <tex>ABC</tex> можно отделить пространство с точками <tex>\implies</tex> выполняется глобальный критерий. | ||
| + | }} | ||
| + | Будем называть '''хорошими''' те рёбра, для которых выполняется локальный критерий Делоне. | ||
| + | {{Лемма | ||
| + | |about=4 | ||
| + | |id=fliplemmasphere | ||
| + | |statement= | ||
| + | Из двух рёбер, которые можно провести для пары треугольников, как минимум одно хорошее. | ||
| + | |proof= | ||
| + | }} | ||
| + | |||
{{nohate2}} | {{nohate2}} | ||
{{wasted}} | {{wasted}} | ||
Текущая версия на 23:21, 28 ноября 2016
| Утверждение: |
Критерии Делоне для ребер и треугольников равносильны. |
|
Из треугольника в ребра: если для каждого треугольника выполнен критерий, то для каждого ребра можно рассматривать плоскость при любом треугольнике при ребре. Обратно: Рассмотрим треугольник , для каждого из ребра можно провести плоскость и они образуют трехмерный угол, снаружи которого нет точек. В пересечении угла и плосокости образуется тетраэдр. Если в нем есть точки, то точки есть внутри треугольника, тогда это не триангуляция точек в тетраэдре нет плоскостью можно отделить пространство с точками выполняется глобальный критерий. |
Будем называть хорошими те рёбра, для которых выполняется локальный критерий Делоне.
| Лемма (4): |
Из двух рёбер, которые можно провести для пары треугольников, как минимум одно хорошее. |
| НЯ! Эта статья полна любви и обожания. Возможно, стоит добавить ещё больше? |
| Задача: |
| Есть один станок и работ. Для каждой работы заданы время выполнения дедлаин и стоимось выполнения этой работы . Необходим минимизировать . |
Содержание
Решение
Применим для решения данной задачи динамическое программирование.
Обозначим . Для всех и будем рассчитывать — значение целевой функции, при условии, что были рассмотрены первые работ и общее время выполнения тех из них, что будут закончены вовремя, не превышает времени .
- Если и работа успевает выполниться вовремя в расписании, соответствующем , то , иначе .
- Если , то , поскольку все работы с номерами , законченные позже, чем , будут выполнены с опозданием.
Отсюда, получим соотношение:
В качестве начальных условий следует взять при и при .
Ответом на задачу будет .
Приведенный ниже алгоритм вычисляет для и . За обозначим самое большое из времен выполнения заданий.
отсортиртировать работы по неубыванию времен дедлайнов = for to for to F_j(t) = \infty for to F_0(t) = 0 for to for to if else for to
Время работы данного алгоритма — .
Для того, чтобы найти само расписание, по доказанной ниже лемме, нам достаточно найти множество работ, которые будут выполнены с опозданием. Это может быть сделано следующим способом:
t = d_n L = \varnothing for downto if </tex> else
Доказательство корректности и оптимальности
| Лемма: |
Пусть все работы отсортированы в порядке неубывания дедлайнов .
Тогда существует оптимальное расписание вида , такое, что — номера работ, которые успеют выполниться вовремя, а — номера просроченных работ. |
| Доказательство: |
|
Пусть у нас есть некоторое оптимальное раписание . Получим необходимое нам расписание путем переставления некоторых работ.
|
См. также
Источники информации
- P. Brucker. Scheduling Algorithms (2006), 5th edition, стр. 26 - 28