Аффинное пространство

Неформальное введение

Аффинное пространство можно воспринимать как векторное пространство, в котором потеряли начальную точку.

Представим, что Алиса знает настоящую начальную точку, а Боб думает, что начальная точка это [math]p[/math]. Есть какие-то два вектора [math]a[/math] и [math]b[/math], и Алиса с Бобом их складывают. Алиса, опираяющаяся на настоящую начальную точку, получит [math]a + b[/math], а Боб, откладывая те же вектора от точки [math]p[/math], получит [math]p + (a - p) + (b - p)[/math], понятно, что результаты будут разные.

Точно так же они могут вычислять линейные комбинации этих векторов, и, как правило, получать разные результаты. Однако, если сумма коэффициентов линейной комбинации будет равна [math]1[/math], то результаты будут получаться одинаковые. Алиса будет получать получать [math]\lambda a + (1 - \lambda) b[/math], и Боб будет точно так же получать [math]p + \lambda(a - p) + (1 - \lambda)(b - p) = \lambda a + (1 - \lambda) b[/math].

У Боба с Алисой есть знание об "аффинной структуре" пространства, то есть значения аффинных комбинаций, определённых как линейные комбинации в которых сумма коэффициентов равна [math]1[/math]. Пространство с аффинной структурой и есть аффинное пространство.

Определение

Определение:

Аффинное пространство – это множество [math]A[/math], ассоциированное с векторным пространством [math]V[/math] над полем [math]K[/math] и свободным действием аддитивной группы [math]V[/math].

Элементы аффинного пространства [math]A[/math] называются точками, элементы векторного пространства [math]V[/math] – векторами.

Другим языком, данное определение говорит, что существует отображение [math](+) : A \times V \rightarrow A[/math], обладающее следующими свойствами:

1. [math]\forall a \in A : a + 0 = a[/math];
2. [math]\forall v, w \in V, a \in A : (a + v) + w = a + (v + w)[/math];
3. Для всех [math]a[/math] из [math]A[/math] отображение [math](a+)[/math] биективно (и для всех [math]v[/math] из [math]V[/math] [math](+v)[/math] тоже биективно).

Последнее свойство позволяет определить вычитание двух элементов из [math]A[/math]. Пусть [math]a, b \in A[/math], тогда [math]b - a[/math] или [math]\overrightarrow{ab}[/math] это такой вектор из [math]V[/math], что [math]a + \overrightarrow{ab} = b[/math]. Таким образом определённое вычитание обладает следующими свойствами:

1. [math]\forall a \in A, v \in V \ \exists ! b \in A : \overrightarrow{ab} = v[/math];
2. [math]\forall a, b, c \in A : \overrightarrow{ab} + \overrightarrow{bc} = \overrightarrow{ac}[/math].

Базисы

Определение:

Набор векторов [math]\{\vec{e}_i\}_{i=1}^n[/math] называется линейно независимым (ЛНЗ), если его линейная комбинация [math]\sum_{i=1}^n \alpha_i \vec{e}_i[/math] равна нулю только в том случае, если она тривиальная, то есть [math]\forall i : \alpha_i = 0[/math].

Определение:

Векторное пространство называется [math]d[/math]-мерным, если в нём существует набор из [math]d[/math] линейно независимых векторов, и не существует набора из [math]d + 1[/math] линейно независимого вектора.

Единственность

Утверждение:

В [math]d[/math]-мерном пространстве любой вектор [math]\vec{A}[/math] единственным образом раскладывается в базисе из [math]d[/math] линейно независимых векторов [math]\{\vec{e}_i\}_{i=1}^d[/math] как [math]\sum_{i=1}^d\alpha_i\vec{e}_i[/math].

[math]\triangleright[/math]

Если мы добавим в базис вектор [math]\vec{A}[/math], то он обязательно станет линейно зависимым, и, значит, найдутся такие [math]\beta[/math] и [math]\{\alpha_i\}[/math], что [math]\displaystyle \beta \vec{A} + \sum_{i=1}^d\alpha_i\vec{e}_i=0 \implies \vec{A} = \sum\limits_{i=1}^d-\frac{\alpha_i}{\beta}\vec{e}_i[/math], и, значит, разложение существует. Теперь пусть есть два разложения [math]\sum_{i=1}^d\alpha_i\vec{e}_i=\vec{A}[/math] и [math]\sum_{i=1}^d\beta_i\vec{e}_i=\vec{A}[/math]. Тогда [math]\displaystyle \vec{A} - \vec{A} = \vec{0} = \sum_{i=1}^d(\alpha_i - \beta_i)\vec{e}_i[/math], однако такое может быть только в том случае, если линейная комбинация тривиальная, то есть [math]\alpha_i - \beta_i = 0 \implies \alpha_i = \beta_i \implies[/math]   разложение единственно.

[math]\triangleleft[/math]

Матрица перехода

Мы можем переходить из одного базиса в другой. Пусть у нас есть базисы [math]\{\vec{e}_i\}_{i=1}^d[/math] и [math]\{\vec{f}_i\}_{i=1}^d[/math].

[math]\displaystyle \vec{A} = \sum_{i=1}^d\alpha_i\vec{e}_i = \sum_{i=1}^d\beta_i\vec{f}_i \ \land\ \vec{e}_i = \sum_{j=1}^d c_{ij}\vec{f}_j[/math]

[math]\displaystyle \vec{A} = \sum_{i=1}^d\alpha_i\vec{e}_i = \sum_{i=1}^d \alpha_i \sum_{j=1}^d c_{ij} \vec{f}_j = \sum_{j=1}^d \vec{f}_j \sum_{i=1}^d \alpha_i c_{ij}[/math]

[math]\displaystyle \beta_j = \sum_{i=1}^d\alpha_i c_{ij} \implies \begin{pmatrix} \beta_1 \\ \beta_2 \\ \vdots \\ \beta_d \end{pmatrix} = \begin{pmatrix} c_{11} & c_{21} & \cdots & c_{d1} \\ c_{12} & c_{22} & \cdots & c_{d2} \\ \vdots & \vdots & \ddots & \vdots \\ c_{1d} & c_{2d} & \cdots & c_{dd} \end{pmatrix} \cdot \begin{pmatrix} \alpha_1 \\ \alpha_2 \\ \vdots \\ \alpha_d \end{pmatrix} [/math]

Вычисление поворота

Матрица поворота

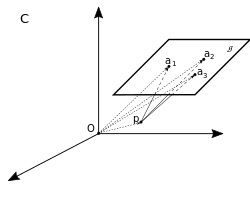
У нас есть гиперплоскость [math]g[/math] и точки задающие её. В [math]d[/math] мерном пространстве у нас будет [math]d[/math] линейно независимых (ЛНЗ) точек [math]a_1, a_2, \dots, a_d[/math]. Линейную независимость точек воспринимаем творчески.

Определение:

Будем называть набор из [math]d[/math] точек линейно независимым, если мы можем выбрать одну из них, провести вектора от нее до всех остальных и получить [math]d-1[/math] ЛНЗ вектор.

Возьмем в нашем пространстве еще одну выделенную точку [math]p[/math]. Получившийся набор [math]a_1, a_2, \dots, a_d, p[/math] тоже будет ЛНЗ.

Пусть у нас есть какая-то выделенная зарание система координат [math]C[/math]. Эта система приходит обычно вместе с какой-то задачей, и обычно она декартова. И у нас тоже будет сейчас декартова.

Мы знаем, что можно составить матрицу перехода, если умеем выразить координаты векторов в исходной базовой системе координат [math]C[/math]. А в нашем случае мы это сделать, конечно, можем: поскольку вектор существует между любыми парами точек, просто сопредставим нашим точкам вектора, соединяющие начало координат [math]O[/math] и очередную точку. Значит, если нам известны координаты точек, то нам известны координаты векторов в ситеме [math]C[/math]. Запишем матрицу перехода и немножко преобразуем её:

Пример для [math]R^3[/math]

[math]A = \begin{pmatrix} \overrightarrow{Oa_1} - \overrightarrow{Op} \\ \overrightarrow{Oa_2} - \overrightarrow{Op} \\ \vdots \\ \overrightarrow{Oa_d} - \overrightarrow{Op} \end{pmatrix}^ \mathrm{T} = \begin{pmatrix} a_1 - p \\ a_2 - p\\ \vdots \\ a_d - p \end{pmatrix}^ \mathrm{T} = \begin{pmatrix} a_1 & 1 \\ a_2 & 1\\ \vdots & \vdots \\ a_d & 1 \\ p & 1 \end{pmatrix}^ \mathrm{T}[/math]

В дальнейшем нас будут интересовать детерминант этой матрицы и его знак:

[math]\det(A) = \begin{vmatrix} a_1 & 1 \\ a_2 & 1\\ \vdots & \vdots \\ a_d & 1 \\ p & 1 \end{vmatrix}[/math]

Обоснование

Лемма:

Точка [math]p[/math] лежит на плоскости [math]g[/math] тогда и только тогда, когда определитель матрицы [math]A[/math] равен [math]0[/math].

Доказательство:

[math]\triangleright[/math]

Плоскость [math]g[/math] определяется замыканием набора [math]a_1, a_2, \dots, a_d[/math] ЛНЗ точек, значит, если [math]p[/math] принадлежит множеству, то [math]p[/math] является линейной комбинацией этих точек. В этом случае мы с помощью преобразований можем получить нулевую стррочку в матрице [math]A[/math], значит, ее определитель будет ноль.

[math]\triangleleft[/math]

Разобъем все точки пространства (кроме тех, что лежат на плоскости) на два множества в зависимости от того, какой знак для них будет иметь детерминант [math]A[/math]. Покажем, что наша классификация осмысленна.

Лемма:

Получившиеся множества будут выпуклыми.

Доказательство:

[math]\triangleright[/math]

По определению выпуклого множества. Возьмем две любые точки [math]p_1[/math] и [math]p_2[/math], лежащие в одной области. По аксиоматике существует вектор [math]\overrightarrow{p_1p_2}[/math] и по определению можно сделать линейную комбинацию. Значит можем получить любую точку между [math]p_1[/math] и [math]p_2[/math], лежащую с ними на одной прямой, отложив от [math]p_1[/math] вектор [math]\alpha \overrightarrow{p_1p_2}[/math], где [math]\alpha \in [0..1][/math]. Если подставить это в определитель, то получим [math]\begin{vmatrix} a_1 & 1 \\ a_2 & 1\\ \dots \\ a_d & 1 \\ p_1 + \alpha\overrightarrow{p_1p_2} & 1 \end{vmatrix} = \begin{vmatrix} a_1 & 1 \\ a_2 & 1\\ \dots \\ a_d & 1 \\ \alpha p_2 + (1 - \alpha)p_1 & 1 \end{vmatrix} = \alpha \begin{vmatrix} a_1 & 1 \\ a_2 & 1\\ \dots \\ a_d & 1 \\ p_2 & 1 \end{vmatrix} + (1 - \alpha) \begin{vmatrix} a_1 & 1 \\ a_2 & 1\\ \dots \\ a_d & 1 \\ p_1 & 1 \end{vmatrix} [/math] Матрицы одинакового знака, и стоящие перед ними коэффициенты положительны. Значит, у нашей точки будет тот же знак определителя, что и у [math]p_1[/math] и [math]p_2[/math].

[math]\triangleleft[/math]

Хорошая лемма, пользоваться мы ей, конечно, не будем.

Проблема в том, что нужно показать, что любая непрерывная кривая не может пройти из точки одного множества в точку другого множества не пересекая плоскость. Но для этого нам необходимо понятие непрерывности, а непрерывность связана с топологией. А у нас есть только афинное пространство, но нет топологии. Пример с Парижской железнодорожной метрикой. TOTO

Можно было бы воспользоваться аналогом леммы Жордана о том, что любая замкнутая кривая без самопересечений делит пространство на две области, но у нас нет области, потому что понятие области связано с топологией.

В афинном пространстве можно вполне естественно ввести евклидовскую метрику: ввести скалярное произведение, а затем показать, что корень из скалярного произведения задает метрику. Тогда эта метрика будет индуцировать топологию открытыми шарами, а значит, можно будет воспользоваться аналогом теоремы Жордана.

Эта история о том, что даже когда мы притворяемся, что у нас нет метрики, мы неявно испоользуем топологию, индуцированную этой метрикой. Но, метрика, не единственна, и топология не единственна. Иногда нам достаточно топологии, которая даже может быть не индуцирована метрикой, или которая вообще не метризуема, но эта топология будет давать свойство непрерывности. Но тогда для нашей топогогии нужно будет доеказывать вышеупомянутый факт (про непрерывность кривой).

Итак, поворот классифицирует точки не лежащие на плоскости и разбивает их на два выпуклых множества