Действие перестановки на набор из элементов, представление в виде циклов

Перестановка — это отображение [math]\pi:X\rightarrow X[/math], которое каждому [math]x_i \in X[/math] ставит во взаимно-однозначное соответствие [math]x_j \in X[/math]

Индексы [math]i,j \in \mathcal{f}1, 2, \ldots, n\mathcal{g}[/math], где [math]n = \mathcal{j}X\mathcal{j}[/math]. Число [math]~n[/math] называют порядком перестановки. Перестановку можно записать в виде упорядоченного набора из чисел [math]1, 2,\ldots, n[/math]. Элемент такого набора [math]~\lt a_1,a_2,\ldots,a_n\gt ~ a_k[/math] означает, что [math]~\pi (x_{a_k}) = x_k [/math]. Таким образом, если [math] \Theta = \lt x_1,x_{2},\ldots,x_{n}\gt [/math] — упорядоченный набор элементов из множества[math]~X[/math], то [math]\pi (\Theta) = \lt x_{q_1},x_{q_2},\ldots,x_{q_n}\gt [/math], где [math]q_{a_i} = i[/math]. Например, применив перестановку [math]~\lt 3,2,4,1\gt [/math] к набору элементов [math]~(x_1,x_2,x_3,x_4)[/math], получим набор [math]~\lt x_4,x_2,x_1,x_3\gt [/math]. <br\>

Произведение перестановок

Произведением перестановок [math]~\pi[/math] и [math]~\sigma[/math] называется композиция (т.е. последовательное применение) этих перестановок: [math](\pi*\sigma)(\Theta) = \pi(\sigma(\Theta)) = \pi \circ \sigma (\Theta)[/math]. Легко показать, что произведение перестановок тоже является перестановкой, причем если [math]~\phi = \pi*\sigma[/math], то [math]\phi(x_i) = \pi \circ \sigma (x_i)[/math].

Циклы

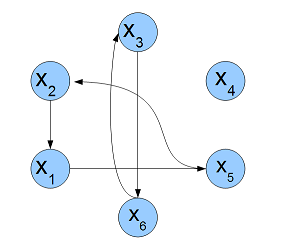
Циклом длины [math]~l[/math] называется такая перестановка [math]~\pi,[/math] которая тождественна на всём множестве [math]X,[/math] кроме подмножества [math]\{x_1,x_2,\dots,x_l\}\subset X[/math] и [math]~\pi(x_l)=x_1,[/math] [math]~\pi(x_i)=x_{i+1}.[/math] Обозначается [math](x_1,x_2,\dots,x_l).[/math] Перестановку также можно записать в виде произведения непересекающихся циклов, причём единственным образом с точностью до порядка следования циклов в произведении. Например: [math]~(1, 5, 2)(3, 6)(4)=\lt 5,1,6,4,2,3\gt [/math].

Перестановку можно представить в виде графа. Граф содержит ребро от вершины [math]~x_i[/math] к вершине [math]~x_j[/math] если [math]~\pi(x_j) = x_i[/math], то есть элемент [math]~x_i[/math] переходит в [math]~x_j[/math] после применения перестановки [math]~\pi[/math]. Тогда циклы перестановки соответствуют циклическим путям в графе.