Связь максимального паросочетания и минимального вершинного покрытия в двудольных графах — различия между версиями
| Строка 1: | Строка 1: | ||
==Определения== | ==Определения== | ||
| − | {{Определение | + | {{Определение|definition= |
Паросочетанием <tex>M</tex> <tex>(matching)</tex> в графе <tex>G</tex> называется такое подмножество множества ребер графа <tex>Е</tex>, | Паросочетанием <tex>M</tex> <tex>(matching)</tex> в графе <tex>G</tex> называется такое подмножество множества ребер графа <tex>Е</tex>, | ||
что каждая вершина <tex>G</tex> инцидентна<br/> не более чем одному ребру из <tex>M</tex>. | что каждая вершина <tex>G</tex> инцидентна<br/> не более чем одному ребру из <tex>M</tex>. | ||
}} | }} | ||
| − | + | ||
| − | {{Определение | + | {{Определение|definition= |
Максимальным паросочетанием <tex>MM</tex> <tex>(maximum</tex> <tex>matching)</tex> в графе <tex>G</tex> называется паросочетание | Максимальным паросочетанием <tex>MM</tex> <tex>(maximum</tex> <tex>matching)</tex> в графе <tex>G</tex> называется паросочетание | ||
максимальной мощности. | максимальной мощности. | ||
| Строка 11: | Строка 11: | ||
| − | {{Определение | + | {{Определение|definition= |
Вершинным покрытием <tex>VC</tex> <tex>(vertex</tex> <tex>covering)</tex> графа <tex>G</tex> называется такое подмножество множества вершин графа <tex>V</tex>, что каждому ребру <tex>G</tex><br/> инцидентна хотя бы одна вершина из <tex>VC</tex>. | Вершинным покрытием <tex>VC</tex> <tex>(vertex</tex> <tex>covering)</tex> графа <tex>G</tex> называется такое подмножество множества вершин графа <tex>V</tex>, что каждому ребру <tex>G</tex><br/> инцидентна хотя бы одна вершина из <tex>VC</tex>. | ||
}} | }} | ||
| − | {{Определение | + | {{Определение|definition= |
Минимальным вершинным покрытием <tex>MVС</tex> <tex>(minimum</tex> <tex>vertex</tex> <tex>covering)</tex> графа <tex>G</tex> называется вершинное покрытие минимальной мощности. | Минимальным вершинным покрытием <tex>MVС</tex> <tex>(minimum</tex> <tex>vertex</tex> <tex>covering)</tex> графа <tex>G</tex> называется вершинное покрытие минимальной мощности. | ||
}} | }} | ||
| Строка 23: | Строка 23: | ||
}} | }} | ||
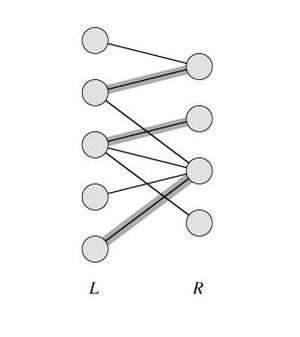
| + | [[Файл:Matching.jpg|thumb|right|Пример максимального паросочетания]] | ||
Версия 16:10, 15 декабря 2010
Определения
| Определение: |
| Паросочетанием в графе называется такое подмножество множества ребер графа ,
что каждая вершина инцидентна не более чем одному ребру из . |
| Определение: |
| Максимальным паросочетанием в графе называется паросочетание максимальной мощности. |
| Определение: |
| Вершинным покрытием графа называется такое подмножество множества вершин графа , что каждому ребру инцидентна хотя бы одна вершина из . |
| Определение: |
| Минимальным вершинным покрытием графа называется вершинное покрытие минимальной мощности. |
Связь MM и MVC в двудольном графе
| Теорема: |
В произвольном двудольном графе мощность максимального паросочетания равна мощности минимального вершинного покрытия. |