Примеры сведения к задачам поиска потока — различия между версиями
| Строка 51: | Строка 51: | ||
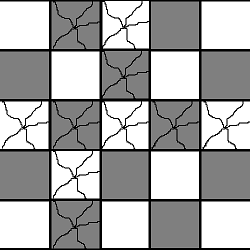
[[Файл:Parquet_example_2.png|Пример раскраски]] | [[Файл:Parquet_example_2.png|Пример раскраски]] | ||
| − | Сначала проверим, что <tex>2 | + | Сначала проверим, что <tex>2 \times B>A</tex>. Если это условие не выполнено, то все выгодней замостить только плитками <tex>1 \times 1</tex> и больше нечего считать. Теперь на нужно максимизировать количество плиток ценой <tex>A</tex>. |
| − | Раскрасим наш паркет по принципу шахматной доски, тогда один конец плитки <tex>2 \times 1</tex> будет лежать на черной клетке, другой — на белой. Итак, построим двудольный граф, одна доля которого будет содержать белые клетки, другая — черные. Ребра весом в <tex>1</tex> проведем между граничащими клетками. Добавим исток с ребрами в белые вершины весом в бесконечность и сток с ребрами из черных клеток весом тоже в бесконечность. Пускай <tex>f</tex> — величина найденного максимального потока между истоком и стоком, это и будет количество плиток <tex>2 \times 1</tex>. Ответом к задаче будет величина <tex>f | + | Раскрасим наш паркет по принципу шахматной доски, тогда один конец плитки <tex>2 \times 1</tex> будет лежать на черной клетке, другой — на белой. Итак, построим двудольный граф, одна доля которого будет содержать белые клетки, другая — черные. Ребра весом в <tex>1</tex> проведем между граничащими клетками. Добавим исток с ребрами в белые вершины весом в бесконечность и сток с ребрами из черных клеток весом тоже в бесконечность. Пускай <tex>f</tex> — величина найденного максимального потока между истоком и стоком, это и будет количество плиток <tex>2 \times 1</tex>. Ответом к задаче будет величина <tex>f \times A+(K-f) \times B</tex>, где <tex>K</tex> — общее количество испорченных клеток. |
==Пример №3. Коллекционер монет.== | ==Пример №3. Коллекционер монет.== | ||
| Строка 59: | Строка 59: | ||
}} | }} | ||
===Решение=== | ===Решение=== | ||
| − | Построим сеть следующего вида: создадим для каждого типа монет по одной вершине, эти вершины будут соответствовать вашим монетам. Нужно собрать как можно больше уникальных монет, поэтому проведем ребро пропускной способности <tex>1</tex> в сток из каждой такой вершины. В вершины, соответствующие монетам, которые у Вас есть изначально, проведем ребро, пропускная способность которого равна количеству таких монет у вас. Для каждого члена клуба (кроме вас) заведем по одной вершине. Эта вершина может принимать не более одной монеты, которой у него нет и отдавать не более <tex>k-1</tex> монеты, которых у него <tex>k | + | Построим сеть следующего вида: создадим для каждого типа монет по одной вершине, эти вершины будут соответствовать вашим монетам. Нужно собрать как можно больше уникальных монет, поэтому проведем ребро пропускной способности <tex>1</tex> в сток из каждой такой вершины. В вершины, соответствующие монетам, которые у Вас есть изначально, проведем ребро, пропускная способность которого равна количеству таких монет у вас. Для каждого члена клуба (кроме вас) заведем по одной вершине. Эта вершина может принимать не более одной монеты, которой у него нет и отдавать не более <tex>k-1</tex> монеты, которых у него <tex>k (k > 1)</tex>. Естественно, член клуба отдает одну монету взамен одной полученной. Таким образом, в каждую такую вершину нужно провести ребро пропускной способности <tex>1</tex> из вершин соответствующих монетам, которых нет у этого члена клуба. А из этих вершин нужно провести ребра пропускной способностью <tex>k_i - 1</tex> в вершину <tex>i</tex>, соответствующую монетам, которых у члена клуба больше одной. Построенная сеть отражает процессы обмена в клубе. Максимальный поток в такой сети будет равен максимальному количеству монет, которые могуть быть собраны вами. |
== См.также == | == См.также == | ||
* [[Схема алгоритма Диница]] | * [[Схема алгоритма Диница]] | ||
Версия 10:03, 10 января 2017
Рассмотрим несколько задач, которые решаются путём сведения к задаче о поиске максимального потока в сети.
Содержание
Пример №1. Лабиринт Минотавра
| Задача: |
| Дано поле размером , некоторые клетки поля закрашены. В одной из незакрашенных клеток поля стоит Минотавр, он умеет ходить только по незакрашенным клеткам (из текущей клетки он может пойти только в ту клетку, с которой имеет общую сторону). Какое минимальное количество клеток нужно закрасить, чтобы Минотавр не смог выбраться за пределы поля? |
Сразу скажем, что выбраться за пределы поля эквивалентно тому, что Минотавр может дойти до какой-либо крайней клетки.
Решение и доказательство корректности
| Теорема: |
Минимальное количество клеток, которое нужно закрасить, равно максимальному количеству клеточно-непересекающихся путей из позиции Минотавра до крайних клеток поля. |
| Доказательство: |
| Очевидно, что ответ не больше, чем количество всех путей от Минотавра до крайних клеток. Сделаем ещё более строгое неравенство: ответ не больше, чем максимальное количество клеточно-непересекающихся путей, т.к. если взять какие-нибудь пересекающихся пути и закрасить клетку в позиции, где они пересекаются, то блокируется выход за пределы поля сразу по этим путям. С другой стороны, если закрасить клетку на каком-то из путей, то блокируется только этот путь, т.к. были взяты клеточно-непересекающиеся пути. Значит, ответ не меньше, чем количество таких путей. |
Переход к сети
Рассмотрим сеть, в которой вершинам будут соответствовать незакрашенные клетки поля, соседние незакрашенные клетки соединим ориентированными рёбрами с пропускной способностью . В качестве истока возьмём вершину, которой соответствует клетка Минотавр. Добавим в граф ещё одну вершину — сток, добавим рёбра из вершин, соответствующим крайним клеткам поля, в сток с пропускной способностью . Чтобы пути не пересекались по клеткам, раздвоим каждую вершину графа на вершины: в одну будут только входить рёбра, из другой — только выходить рёбра, и сами эти вершины соединим ребром с пропускной способностью .
Используя алгоритм Форда-Фалкерсона, найдём максимальный поток в сети. Согласно теореме о декомпозиции, нахождение максимального потока эквивалентно тому, что мы нашли максимальное количество путей из истока в сток. Т.е. требуемый ответ на задачу равен максимальному потоку.
Оценка времени работы
Время работы алгоритма Форда-Фалкерсона . Первое замечание: (это следует из того, что из каждой вершины исходит не более рёбер), т.е. . Второе замечание: ответ не превосходит , т.к. можно закрасить клетку слева, справа, сверху и снизу от позиции Минотавра и он не сможет никуда двигаться, поэтому можно считать константой. Итоговое время работы .
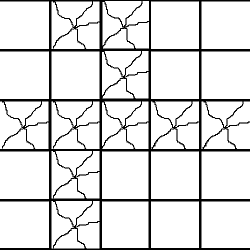
Пример №2. Испорченный паркет.
| Задача: |
| Дан паркет размером , некоторые клетки которого испорчены, их необходимо закрыть новыми плитками. Плитки бывают размером ценой , и ценой . Плитки можно поворачивать, но нельзя разрезать. Какую минимальную сумму нужно потратить, что бы заложить испорченные плитки паркета. Новые плитки не должны перекрывать никакие другие плитки. |
Решение
Сначала проверим, что . Если это условие не выполнено, то все выгодней замостить только плитками и больше нечего считать. Теперь на нужно максимизировать количество плиток ценой . Раскрасим наш паркет по принципу шахматной доски, тогда один конец плитки будет лежать на черной клетке, другой — на белой. Итак, построим двудольный граф, одна доля которого будет содержать белые клетки, другая — черные. Ребра весом в проведем между граничащими клетками. Добавим исток с ребрами в белые вершины весом в бесконечность и сток с ребрами из черных клеток весом тоже в бесконечность. Пускай — величина найденного максимального потока между истоком и стоком, это и будет количество плиток . Ответом к задаче будет величина , где — общее количество испорченных клеток.
Пример №3. Коллекционер монет.
| Задача: |
| Есть коллекционеров и видов монет. Для вступления в клуб, необходимо иметь не меньше одной монеты каждого типа. Вы (у вас номер 1) можете меняться с коллекционерами имеющимися монетами. Любой коллекционер обменяет монету свою монету на вашу монету , если у него больше одной монеты типа и нету ни одной монеты типа . Вы, в свою очередь, можете нарушать это правило. Нужно набрать как можно больше типов монет по известной ситуации у всех коллекционеров. |
Решение
Построим сеть следующего вида: создадим для каждого типа монет по одной вершине, эти вершины будут соответствовать вашим монетам. Нужно собрать как можно больше уникальных монет, поэтому проведем ребро пропускной способности в сток из каждой такой вершины. В вершины, соответствующие монетам, которые у Вас есть изначально, проведем ребро, пропускная способность которого равна количеству таких монет у вас. Для каждого члена клуба (кроме вас) заведем по одной вершине. Эта вершина может принимать не более одной монеты, которой у него нет и отдавать не более монеты, которых у него . Естественно, член клуба отдает одну монету взамен одной полученной. Таким образом, в каждую такую вершину нужно провести ребро пропускной способности из вершин соответствующих монетам, которых нет у этого члена клуба. А из этих вершин нужно провести ребра пропускной способностью в вершину , соответствующую монетам, которых у члена клуба больше одной. Построенная сеть отражает процессы обмена в клубе. Максимальный поток в такой сети будет равен максимальному количеству монет, которые могуть быть собраны вами.