Классы Sharp P, Sharp P-Complete

Классы #P и #P-Complete

Определение:

[math]\#P[/math] представляет класс задач, решением которых является количество успешных (завершающихся в допускающих состояниях) путей вычислений для недетерминированной МТ, работающей за полиномиальное время. Отличается от большинства рассмотренных классов тем, что задачи требуют в качестве ответа не [math]``0"[/math] или [math]``1"[/math], а натуральное число. Более формально: [math]f : \{0,1\}^* \rightarrow \mathbb{N}[/math] принадлежит [math]\#P[/math], если существует [math]p \in Poly[/math] и машина Тьюринга [math]M[/math] такая, что для любого [math]x \in \{0,1\}^* : f(x) = | \{y \in \{0,1\}^{p(|x|)} : M(x,y) = 1 \} |[/math].

Вопрос, являются ли задачи из [math]\#P[/math] //эффективно разрешимыми// остается открытым. Класс [math]FP[/math] - аналог класса [math]P[/math] для задач, ответ на которые представляется не битовым значением, а натуральным числом. Подсчет числа сертификатов как минимум столь же сложно, как и проверка наличия сертификата, а значит, если доказать равенство [math]\#P=FP[/math], то автоматически будет доказано [math]NP=P[/math]. Однако из [math]NP=P[/math] вовсе не следует [math]\#P=FP[/math]. Если [math]PSPACE = P[/math], то [math]\#P=FP[/math], так как подсчет числа сертификатов может быть выполнен за полиномиальную память.

Примеры задач из #P

• #SAT
• [math]\#CYCLE[/math] - имея ориентированный граф [math]G[/math], посчитать число простых циклов. Аналогичная задача, отвечающая на вопрос, существует ли в заданном ориентированном графе простой цикл, может быть решена за линейное время при помощи поиска в ширину. Проблема подсчета значительно сложнее.

Теорема:

Если [math]\#CYCLE \in FP[/math], тогда [math]P=NP[/math].

Доказательство:

[math]\triangleright[/math]

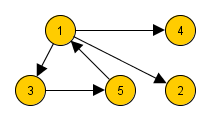
[math]deg^{-}+deg^{+}=10=2\cdot |E|[/math] Для графа [math]G[/math] с n вершинами построим граф [math]G'[/math] такой, что в [math]G[/math] есть Гамильтонов цикл тогда и только тогда, когда в [math]G'[/math] есть [math]n^{n^2}[/math] циклов. Чтобы получить [math]G'[/math], заменим каждое ребро [math](u,v)[/math] из [math]G[/math] на блок [math]H[/math]. Блок состоит из [math]m = n * \log{n} + 1[/math] уровней. [math]G[/math] представляет из себя ацикличный граф, а значит циклы в [math]G'[/math] соответствуют циклам в [math]G[/math]. Кроме того, существует [math]2^m[/math] различных путей между [math]u[/math] и [math]v[/math] внутри блока, следовательно простому циклу длины [math]l[/math] в [math]G[/math] соответствует цикл длины [math]2^{(ml)}[/math] в [math]G'[/math]. Заметим, что если граф [math]G[/math] содержит гамильтонов цикл, то в [math]G'[/math] существует минимум [math]2^{m(n-1)} \gt n^{n^2}[/math] циклов. Проверим в обратную сторону. Если в [math]G[/math] не существует Гамильтонова цикла, то самый длинный цикл в [math]G[/math] имеет длину не больше [math]n-1[/math] и число циклов не может превысить [math]n^{n-1}[/math]. Таким образом, в [math]G'[/math] будет не более чем [math](2^m)^{n-1} * n^{n-1} \lt n^{n^2}[/math] циклов.му входящих и на единицу сумму исходящих степеней. Таким образом, сумма входящих и исходящих степеней всех вершин ориентированного графа чётна и равна удвоенному числу рёбер. Преобразование графа [math]G[/math] в [math]G'[/math] можно выполнить за полином от количества вершин. Таким образом, если [math]\#CYCLE \in FP[/math], тогда сразу же [math]HAM \in P[/math]. А так как[math] HAM \in NP[/math], то [math]NP = P[/math].

[math]\triangleleft[/math]