Техника частичного каскадирования — различия между версиями
(Синтаксические поправочки ч3) |
(Добавлена часть "ответ на запрос", требуется немного дописать) |
||
| Строка 44: | Строка 44: | ||
<br>''Первый этап построения'': | <br>''Первый этап построения'': | ||
<br> <tex> i = k </tex> : Данный каталог не имеет никаких ссылок и равен <tex> C_i </tex>. | <br> <tex> i = k </tex> : Данный каталог не имеет никаких ссылок и равен <tex> C_i </tex>. | ||
| − | <br> <tex> i < k </tex> : Для построения данного каталога будем сливать каталог <tex> C_i </tex> с каждым вторым элементом каталога <tex> M_{i + 1} </tex>. Каждый элемент из каталога <tex> M_{i + 1} </tex> оснастим ссылкой на позицию, откуда мы его взяли. | + | <br> <tex> i < k </tex> : Для построения данного каталога будем сливать каталог <tex> C_i </tex> с каждым вторым элементом каталога <tex> M_{i + 1} </tex>. Каждый элемент из каталога <tex> M_{i + 1} </tex> оснастим ссылкой на позицию, откуда мы его взяли, такие ссылки будет называть ссылками вниз. |
<br>''Второй этап построения'': | <br>''Второй этап построения'': | ||
| − | <br> В каждом ''модифицированном каталоге'' для каждого элемента заведем две ссылки. Для ''неподставных элементов'' это будут ссылки на минимальный ''подставной элемент'' больше текущего и на максимальный ''подставной элемент'' меньше текущего. И наоборот, если ''элемент подставной'', то ссылки будут на минимальный ''неподставной элемент'' больше текущего и на максимальный ''неподставной элемент'' больше текущего. | + | <br> В каждом ''модифицированном каталоге'' для каждого элемента заведем две ссылки. Для ''неподставных элементов'' это будут ссылки на минимальный ''подставной элемент'' больше текущего и на максимальный ''подставной элемент'' меньше текущего. И наоборот, если ''элемент подставной'', то ссылки будут на минимальный ''неподставной элемент'' больше текущего и на максимальный ''неподставной элемент'' больше текущего. Назовем их ссылками влево и вправо. |
<br> Рассмотрим на процесс построения на примере. | <br> Рассмотрим на процесс построения на примере. | ||
| Строка 59: | Строка 59: | ||
=== Ответ на запрос === | === Ответ на запрос === | ||
| + | |||
| + | В каталоге <tex> C_1 </tex> ответ на запрос найдем с помощью бинарного поиска по <tex> С_1 </tex>. Пусть ответом для этого каталога будет ячейка <tex> cell </tex>. Далее проитерируемся по оставшимся каталогам. Для того, чтобы перейти в новый модифицированный каталог мы перейдем из <tex> cell </tex> по ссылке влево, чтобы попасть в подставную вершину, а потом из нее перейдем по ссылке вниз, чтобы попасть в следующий каталог. Если теперь <tex> cell </tex> - неподставная вершина, то нам достаточно рассмотреть двух ее соседей справа в <tex> C_i </tex>, так как <tex> cell.key < x </tex>, а каждая вторая ячейка из <tex> M_i </tex> попадает в <tex> M_{i - 1} </tex>, т.е. мы бы встретили ее ранее. | ||
Версия 20:20, 7 июня 2017
| Определение: |
| Каталог — упорядоченный массив из элементов, на которых введено отношение порядка. В данной статье предполагается, что массив упорядочен по неубыванию. |
Техника частичного каскадирования (англ. fractional cascading technique) — это способ организации структуры данных, который предназначен для быстрого итеративного поиска в каталогах.
| Задача: |
| Дано каталогов , каталог имеет размер . Поступают запросы, которые представляют собой один элемент . Требуется для каждого запроса определить в каждом каталоге максимальный элемент меньше либо равный . |
Содержание
Различные подходы к решению
Пусть .
1) Для ответа на запрос последовательно посетим все каталоги. Пусть мы находимся в -ом каталоге, тогда мы можем ответить на запрос для данного каталога за , используя бинарный поиск. Так как каталогов штук, то для ответа на запрос понадобится времени. Для хранения всех каталогов понадобится памяти.
2) Для второго способа построим сбалансированное бинарное дерево поиска их всех элементов всех каталогов. В каждой вершине дерева будет хранится дополнительно кортеж из элементов - максимальных представителей каталогов меньше либо равных ключу вершины. Таким образом такая структура будет занимать на дерево поиска и на дополнительные кортежи.Тогда для ответа на запрос найдем в дереве поиска максимальный ключ меньше либо равный и выведем элементов соответствующего кортежа, итого ответ на запрос производится за .
Итого имеем:
| Тип подхода к решению | Необходимая память | Время ответа на один запрос |
|---|---|---|
| |
|
|
| |
|
|
Решение с помощью техники частичного каскадирования
Как будет показано далее, эта техника берет лучшее от подходов к решению этой задачи, что были рассмотрены выше, а именно она требует памяти и времени для ответа на запрос.
Идея данной техники построена на следующем:
1) Мы можем проводить ссылки из каталога номер в -ый каталог таким образом, что разница между элементами, соединенными ссылками минимальна, что, очевидно, в некоторых случаях уменьшит время поиска.
2) Мы можем для оптимизации пункта 1 создать модифицированные каталоги , где -ый каталог будет представлять каталог слитый с
Построение
Рассмотрим подробнее построение каталогов . Введем определения:
| Определение: |
| Подставной элемент — элемент каталога , который пришел из каталога . А также каталоги будем называть модифицированными каталогами. |
Первый этап построения:
: Данный каталог не имеет никаких ссылок и равен .
: Для построения данного каталога будем сливать каталог с каждым вторым элементом каталога . Каждый элемент из каталога оснастим ссылкой на позицию, откуда мы его взяли, такие ссылки будет называть ссылками вниз.
Второй этап построения:
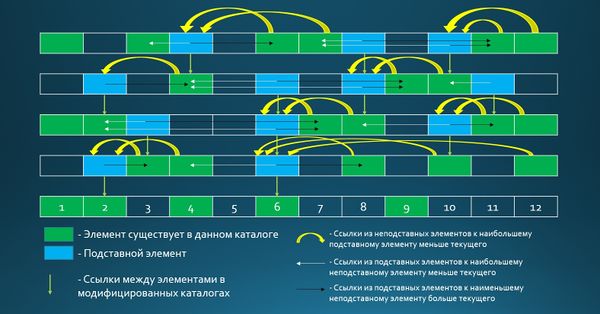
В каждом модифицированном каталоге для каждого элемента заведем две ссылки. Для неподставных элементов это будут ссылки на минимальный подставной элемент больше текущего и на максимальный подставной элемент меньше текущего. И наоборот, если элемент подставной, то ссылки будут на минимальный неподставной элемент больше текущего и на максимальный неподставной элемент больше текущего. Назовем их ссылками влево и вправо.
Рассмотрим на процесс построения на примере.
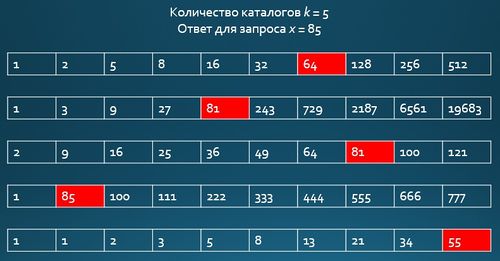
Пусть дано каталогов :
Для наглядности заведем таблицу, где в -ой строке -ая ячейка будет окрашена в зеленый цвет, если она присутствует в каталоге . Тогда результатом построения будет таблица, которая представлена на рисунке (без ссылок из подставных элементов).
Ответ на запрос
В каталоге ответ на запрос найдем с помощью бинарного поиска по . Пусть ответом для этого каталога будет ячейка . Далее проитерируемся по оставшимся каталогам. Для того, чтобы перейти в новый модифицированный каталог мы перейдем из по ссылке влево, чтобы попасть в подставную вершину, а потом из нее перейдем по ссылке вниз, чтобы попасть в следующий каталог. Если теперь - неподставная вершина, то нам достаточно рассмотреть двух ее соседей справа в , так как , а каждая вторая ячейка из попадает в , т.е. мы бы встретили ее ранее.