Панциклический граф — различия между версиями
(Первая часть доказательства) |
|||
| Строка 27: | Строка 27: | ||
Докажем методом от противного, что <tex> n </tex> {{---}} четно. Пусть <tex> n </tex> является нечетным, тогда из рассуждений выше существует вершина <tex> v_x </tex>, для которое верно, что <tex> deg(v_x) \leqslant \genfrac{}{}{}{}{n-1}{2} </tex>. | Докажем методом от противного, что <tex> n </tex> {{---}} четно. Пусть <tex> n </tex> является нечетным, тогда из рассуждений выше существует вершина <tex> v_x </tex>, для которое верно, что <tex> deg(v_x) \leqslant \genfrac{}{}{}{}{n-1}{2} </tex>. | ||
Пусть это не так, тогда <tex> \forall i, 1 \leqslant i \leqslant n : deg(i) \geqslant \genfrac{}{}{}{}{n-1}{2} + 1 = \genfrac{}{}{}{}{n+1}{2} </tex>, значит <tex> \forall j, 1 \leqslant j \leqslant n : deg(v_j) + deg(v_{j+1}) \geqslant \genfrac{}{}{}{}{n+1}{2} + \genfrac{}{}{}{}{n+1}{2} = n + 1 </tex>, то есть мы получили противоречие с тем, что <tex> deg(v_j) + deg(v_{j + 1}) \leqslant n </tex>. | Пусть это не так, тогда <tex> \forall i, 1 \leqslant i \leqslant n : deg(i) \geqslant \genfrac{}{}{}{}{n-1}{2} + 1 = \genfrac{}{}{}{}{n+1}{2} </tex>, значит <tex> \forall j, 1 \leqslant j \leqslant n : deg(v_j) + deg(v_{j+1}) \geqslant \genfrac{}{}{}{}{n+1}{2} + \genfrac{}{}{}{}{n+1}{2} = n + 1 </tex>, то есть мы получили противоречие с тем, что <tex> deg(v_j) + deg(v_{j + 1}) \leqslant n </tex>. | ||
| − | Без потери общности пусть <tex> v_x = v_n </tex> Рассмотрим <tex> 2|E| = \sum\limits_{i=1}^n deg(v_i) = \sum\limits_{i=1}^{(n - 1)/2} (deg(v_{2i-1}) + deg(v_{2i})) + deg(v_n) \leqslant \genfrac{}{}{}{}{n(n-1)}{2} + \genfrac{}{}{}{}{n-1}{2} < </tex> <tex> \genfrac{}{}{}{}{n^2}{2} </tex>, то есть <tex> |E| < \genfrac{}{}{}{}{n^2}{2} </tex>, но по условию <tex> |E| \geqslant n^2/4 </tex> - получили противоречие. Таким образом <tex> n </tex> является четным. | + | Без потери общности пусть <tex> v_x = v_n </tex> Рассмотрим <tex> 2|E| = \sum\limits_{i=1}^n deg(v_i) = \sum\limits_{i=1}^{(n - 1)/2} (deg(v_{2i-1}) + deg(v_{2i})) + deg(v_n) \leqslant \genfrac{}{}{}{}{n(n-1)}{2} + \genfrac{}{}{}{}{n-1}{2} < </tex> <tex> \genfrac{}{}{}{}{n^2}{2} </tex>, то есть <tex> |E| < \genfrac{}{}{}{}{n^2}{2} </tex>, но по условию <tex> |E| \geqslant n^2/4 </tex> - получили противоречие. Таким образом <tex> n </tex> является четным. Тогда верно, что <tex> 2|E| \leqslant \sum\limits_{i=1}^n deg(v_i) = \sum\limits_{i=1}^{n/2} (deg(v_{2i-1}) + deg(v_{2i})) \leqslant \genfrac{}{}{}{}{n^2}{2} </tex>, а так как по условию <tex> |E| \geqslant n^2/4 </tex>, то <tex> |E| = \genfrac{}{}{}{}{n^2}{4} </tex>. Данное равенство достигается, если верно, что: |
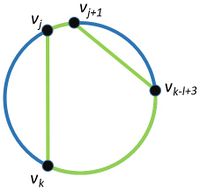
| + | Для <tex>k</tex> таких, что <tex> j + l - 1 \leqslant k \leqslant j + l - 2 </tex> : <tex> (v_j, v_k) \in E </tex> и <tex>(v_{j+1}, v_{k-l+3}) \notin E </tex> | ||
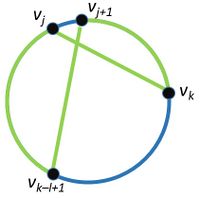
| + | Для <tex>k</tex> таких, что <tex> j + 2 \leqslant k \leqslant j + l - 2 </tex> : <tex>(v_j, v_k) \in E </tex> и <tex>(v_{j+1}, v_{k-l+1}) \notin E </tex> | ||
| + | Пусть <tex> G </tex> не <tex> K_{n/2, n/2} </tex>, тогда | ||
}} | }} | ||
Версия 16:42, 4 декабря 2017
| Определение: |
| Панциклический граф (англ. pancyclic graph) — граф, в котором есть циклы всех длин от до . Если граф содержит все циклы от до , то такой граф называют -панциклическим. |
| Теорема (J. A. Bondy): |
— гамильтонов граф, .
Тогда верно одно из двух утверждений:
|
| Доказательство: |
|
Обозначим как гамильтонов цикл в графе . Для простоты расположим на окружности, тогда ребра не принадлежащие можно считать хордами. Пусть в графе нет цикла длины , (по условию в графе существует гамильтонов цикл, длина которого равна ). Рассмотрим две соседний вершины и вместе с ними рассмотрим следующие пары: Для таких, что рассмотрим пары () и () Для таких, что рассмотрим пары () и () При добавлении таких пар ребер в графе появляется цикл длины , а значить в может входить максимум одно ребро из таких пар. Тогда можно утверждать, что . Докажем методом от противного, что — четно. Пусть является нечетным, тогда из рассуждений выше существует вершина , для которое верно, что . Пусть это не так, тогда , значит , то есть мы получили противоречие с тем, что . Без потери общности пусть Рассмотрим , то есть , но по условию - получили противоречие. Таким образом является четным. Тогда верно, что , а так как по условию , то . Данное равенство достигается, если верно, что: Для таких, что : и Для таких, что : и Пусть не , тогда |
| Теорема (Schmeichel & Hakimi): |
— гамильтонов граф, — его гамильтонов цикл, для которого выполняется неравенство . Тогда — панциклический граф, двудольный граф или граф, в котором нет только цикла длины . |