Лапы и минимальные по включению барьеры в графе — различия между версиями
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
| − | |definition='''Лапой''' называется индуцированный подграф графа <tex>G</tex>, изоморфный двудольному графу <tex>K_{1,\;3}</tex> | + | |id = paw |
| − | }} | + | |definition='''Лапой''' (англ. ''paw'') называется индуцированный подграф графа <tex>G</tex>, изоморфный двудольному графу <tex>K_{1,\;3}</tex>. |
| + | }} [[Файл:Lapa.png|170px|thumb|left|Лапа]] | ||
{{Определение | {{Определение | ||
| − | |definition='''Центр лапы''' {{---}} вершина степени 3 в лапе | + | |id = paw center |
| + | |definition='''Центр лапы''' (англ. ''paw center'') {{---}} вершина степени 3 в лапе. | ||
}} | }} | ||
{{Определение | {{Определение | ||
| − | |definition='''Минимальный по включению [[Декомпозиция Эдмондса-Галлаи#barrier | барьер]] '''(англ.''minimum barrier'') {{---}} барьер минимальной мощности | + | |id = minimum_barrier |
| + | |definition='''Минимальный по включению [[Декомпозиция Эдмондса-Галлаи#barrier | барьер]] '''(англ.''minimum barrier'') {{---}} барьер минимальной мощности. | ||
}} | }} | ||
| Строка 13: | Строка 16: | ||
|statement=Пусть <tex>B</tex> - минимальный по включению барьер <tex>G</tex>, тогда каждая вершина <tex>B</tex> - центр лапы в <tex>G</tex>. | |statement=Пусть <tex>B</tex> - минимальный по включению барьер <tex>G</tex>, тогда каждая вершина <tex>B</tex> - центр лапы в <tex>G</tex>. | ||
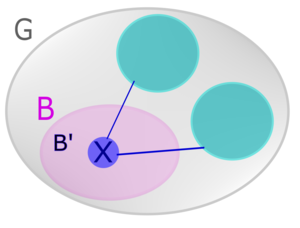
|proof=Пусть <tex>x\in B</tex> не является центром лапы. Тогда <tex>x</tex> смежна не более чем с двумя компонентами связности графа <tex>G \setminus B</tex>.<br> | |proof=Пусть <tex>x\in B</tex> не является центром лапы. Тогда <tex>x</tex> смежна не более чем с двумя компонентами связности графа <tex>G \setminus B</tex>.<br> | ||
| − | Обозначим <tex>B' = B\setminus x</tex><br> | + | Обозначим <tex>B' = B\setminus x</tex>.<br> |
| − | Найдём соотношение между <tex>\mathrm{odd}(G\setminus B')\ </tex> и <tex>\mathrm{odd}(G\setminus B)\ </tex> <br> | + | Найдём соотношение между <tex>\mathrm{odd}(G\setminus B')\ </tex> и <tex>\mathrm{odd}(G\setminus B)\ </tex>. <br> |
| − | Рассмотрим возможные случаи количества компонент связности в <tex>G \setminus B</tex>, с которыми смежна <tex>x</tex>, и посмотрим на их четности(компоненты в <tex>B</tex> нас не интересуют)<br> | + | Рассмотрим возможные случаи количества компонент связности в <tex>G \setminus B</tex>, с которыми смежна <tex>x</tex>, и посмотрим на их четности(компоненты в <tex>B</tex> нас не интересуют).<br> |
| − | # <tex>x</tex> смежна с двумя компонентами связности <tex>G \setminus B</tex>.[[Файл:GraphsForLaps.png|300px|thumb|right|<tex>x</tex> смежна с двумя компонентами связности из <tex>G \setminus B</tex>]]<br> | + | # <tex>x</tex> смежна с двумя компонентами связности <tex>G \setminus B</tex>.[[Файл:GraphsForLaps.png|300px|thumb|right|<tex>x</tex> смежна с двумя компонентами связности из <tex>G \setminus B</tex>]].<br> |
#:a) Одна четная, другая - нечетная. Тогда <tex>\mathrm{odd}(G\setminus B')\ = \mathrm{odd}(G\setminus B)\ - 1 </tex> <br> | #:a) Одна четная, другая - нечетная. Тогда <tex>\mathrm{odd}(G\setminus B')\ = \mathrm{odd}(G\setminus B)\ - 1 </tex> <br> | ||
#:b) Обе чётные : <tex>\mathrm{odd}(G\setminus B')\ = \mathrm{odd}(G\setminus B)\ + 1 </tex> <br> | #:b) Обе чётные : <tex>\mathrm{odd}(G\setminus B')\ = \mathrm{odd}(G\setminus B)\ + 1 </tex> <br> | ||
| Строка 41: | Строка 44: | ||
|statement=Пусть <tex>G</tex> {{---}} связанный граф, не содержащий лапы, <tex>v(G)</tex> чётно. Тогда <tex>G</tex> имеет [[Паросочетания: основные определения, теорема о максимальном паросочетании и дополняющих цепях#perfect_matching | совершенное паросочетание]]. | |statement=Пусть <tex>G</tex> {{---}} связанный граф, не содержащий лапы, <tex>v(G)</tex> чётно. Тогда <tex>G</tex> имеет [[Паросочетания: основные определения, теорема о максимальном паросочетании и дополняющих цепях#perfect_matching | совершенное паросочетание]]. | ||
|proof= Пусть <tex>B</tex> {{---}} минимальный по включению барьер графа <tex>G</tex>. Тогда, по предыдущей теореме имеем <tex>B = \varnothing </tex>.<br> | |proof= Пусть <tex>B</tex> {{---}} минимальный по включению барьер графа <tex>G</tex>. Тогда, по предыдущей теореме имеем <tex>B = \varnothing </tex>.<br> | ||
| − | По условию <tex>G</tex> {{---}} связный граф с чётным числом вершин <tex>\Rightarrow </tex> <tex>\mathrm{odd}(G\setminus \varnothing )\ = 0 </tex> <br> | + | По условию <tex>G</tex> {{---}} связный граф с чётным числом вершин <tex>\Rightarrow </tex> <tex>\mathrm{odd}(G\setminus \varnothing )\ = 0 </tex>. <br> |
<tex>B</tex> {{---}} барьер <tex>\Leftrightarrow \mathrm{odd}(G\setminus \varnothing) - |\varnothing|\ = \mathrm{def}(G) = 0 </tex>. Значит, количество вершин, не покрытых [[Паросочетания: основные определения, теорема о максимальном паросочетании и дополняющих цепях#maximal_matching | максимальным паросочетанием]], равно 0, т.е. существует совершенное паросочетание. | <tex>B</tex> {{---}} барьер <tex>\Leftrightarrow \mathrm{odd}(G\setminus \varnothing) - |\varnothing|\ = \mathrm{def}(G) = 0 </tex>. Значит, количество вершин, не покрытых [[Паросочетания: основные определения, теорема о максимальном паросочетании и дополняющих цепях#maximal_matching | максимальным паросочетанием]], равно 0, т.е. существует совершенное паросочетание. | ||
}} | }} | ||
Версия 02:49, 14 декабря 2017
| Определение: |
| Лапой (англ. paw) называется индуцированный подграф графа , изоморфный двудольному графу . |
| Определение: |
| Центр лапы (англ. paw center) — вершина степени 3 в лапе. |
| Определение: |
| Минимальный по включению барьер (англ.minimum barrier) — барьер минимальной мощности. |
| Теорема: |
Пусть - минимальный по включению барьер , тогда каждая вершина - центр лапы в . |
| Доказательство: |
|
Пусть не является центром лапы. Тогда смежна не более чем с двумя компонентами связности графа .
Рассмотрев случаи, видим, что для любого из них выполнено :
|
| Утверждение (D.P.Sumner, следствие из теоремы): |
Пусть — связанный граф, не содержащий лапы, чётно. Тогда имеет совершенное паросочетание. |
|
Пусть — минимальный по включению барьер графа . Тогда, по предыдущей теореме имеем . |
См. также
- Использование обхода в глубину для поиска цикла
- Использование обхода в глубину для поиска мостов
- Паросочетания: основные определения, теорема о максимальном паросочетании и дополняющих цепях
Источники информации
- Карпов В. Д. - Теория графов, стр 55