Максимальное количество попарно непересекающихся остовных деревьев в графе с n вершинами

Утверждение:

Максимальное количество попарно непересекающихся остовных деревьев в графе с [math]n[/math] вершинами равно [math] \left \lfloor {\dfrac{n}{2}}\right \rfloor [/math]

[math]\triangleright[/math]

Очевидно, что наибольшее количество непересекающихся остовных деревьев может быть только в полном графе из [math]n[/math] вершин. Количество ребер в таком графе равно [math] \dfrac{n(n - 1)}{2}[/math], а в каждом дереве [math]n - 1[/math] ребро. Значит, в полном графе мы сможем построить не более [math] \dfrac{n(n - 1)}{2(n - 1)} = \left \lfloor {\dfrac{n}{2}}\right \rfloor[/math] остовных деревьев. 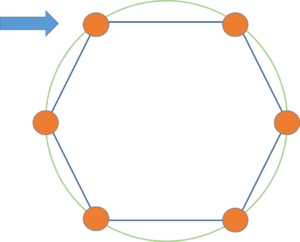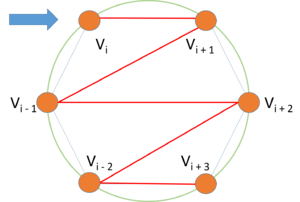Алгоритм построения остовных деревьев. Расположим вершины на окружности так, чтобы они образовывали правильный многоугольник, и выберем начальную вершину (рис.1). Для [math]\left \lfloor {\dfrac{n}{2}}\right \rfloor[/math] вершин по часовой стрелке, начиная с этой вершины, будем строить остовные деревья. Для [math]i[/math]-ой вершины строим такой путь [math]:[/math][math]V_i V_{i+1} V_{i-1} V_{i+2} V_{i-2}\ldots, [/math] — до тех пор, пока не соединим все вершины. Это и будет остовным деревом. (рис.2-3) Рис.1 Стрелкой указана начальная вершина Рис.2 Красным цветом выделено первое построенное остовное дерево Рис.3 Все остовные деревья Докажем, что построенные с помощью такого алгоритма остовные деревья будут попарно непересекающимися. Для этого докажем, что никакие ребра не совпадут. Ребра могут совпасть только в том случае, если дуги, на которые эти ребра опираются, будут одинаковой длины. Заметим, что при построении каждого последующего дерева его ребра получаются из поворотов ребер предыдущего на длину [math] \dfrac{l}{n}[/math], где [math]l[/math] — длина окружности. Рассмотрим первое построенное остовное дерево.(рис.3) В нем не более [math]2[/math]-х ребер имеют одинаковую длину дуги (длина дуги у ребра, расположенного на диаметре окружности, не совпадает с длиной дуги любого другого ребра данного остовного дерева). Значит, повороты только этих ребер могут совпасть между собой. 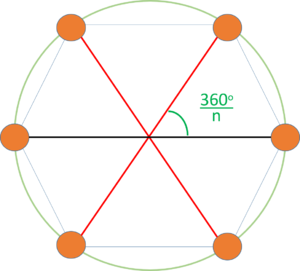Докажем, что повороты ребра, расположенного на диаметре окружности, не совпадут друг с другом (если [math]n[/math] нечетно, то такого ребра не будет). Чтобы хоть какой-то поворот совпал, мы должны повернуть ребро на [math]180 ^{\circ}[/math]. Каждый раз мы поворачиваем ребро на [math]\dfrac{360 ^{\circ}}{n}[/math]. А так как мы поворачиваем ребро [math]\dfrac{n}{2} - 1[/math] раз, то в сумме мы повернем его на [math]\dfrac{360 ^{\circ}}{n} \cdot[/math] [math]([/math][math]\dfrac{n}{2} - 1 [/math][math])[/math] [math]=180 ^{\circ} - \dfrac{360 ^{\circ}}{n} \lt 180 ^{\circ}[/math]. А это значит, что никакие ребра не совпадут друг с другом. 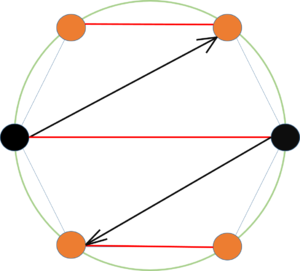(рис.4) Рис.4 Черным цветом выделено рассматриваемое ребро, красным - все его повороты Докажем для остальных ребер. (рис.5) Возьмем ребро, которое не лежит на диаметре окружности. В данном остовном дереве есть ребро, которое имеет такую же длину дуги. Ориентируем данные ребра в сторону часовой стрелки. Чтобы повороты этих ребер совпали, нужно, чтобы совпали их начала и концы. Покажем, что их начала никогда не совпадут. Чтобы начало первого ребра совпало с началом второго, нужно первое ребро повернуть хотя бы на половину длины окружности, то есть на [math] \dfrac{l}{2}[/math]. Для этого нам нужно сделать [math] \dfrac{n}{2} [/math] поворотов: [math] \dfrac{l}{n} \cdot \dfrac{n}{2} = \dfrac{l}{2}[/math]. Но мы делаем только [math] \dfrac{n}{2} - 1[/math] поворот. Аналогично с поворотом второго ребра. Для нечетных [math]n[/math] граф будет неполным, поэтому даже [math] \dfrac{n}{2}[/math] поворотов может не хватить для совпадения ребер. Рис.5 Черным цветом выделены рассматриваемые ребра

[math]\triangleleft[/math]

См. также

• Остовные деревья: определения, лемма о безопасном ребре
• Остовное дерево в планарном графе
• Минимально узкое остовное дерево