Лапы и минимальные по включению барьеры в графе — различия между версиями
| Строка 26: | Строка 26: | ||
}} | }} | ||
| − | + | ||
| − | + | ||
| − | + | ||
{{Теорема | {{Теорема | ||
| Строка 39: | Строка 39: | ||
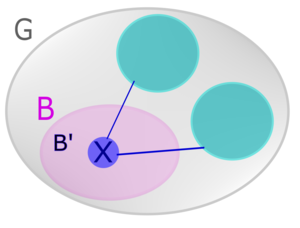
# <tex>x</tex> смежна с двумя компонентами связности графа <tex>G \setminus B</tex>.[[ Файл:GraphsForLaps.png|300px|thumb|right|<tex>x</tex> смежна с двумя компонентами связности графа <tex>G \setminus B</tex> ]] <br> | # <tex>x</tex> смежна с двумя компонентами связности графа <tex>G \setminus B</tex>.[[ Файл:GraphsForLaps.png|300px|thumb|right|<tex>x</tex> смежна с двумя компонентами связности графа <tex>G \setminus B</tex> ]] <br> | ||
#: a) Одна компонента чётная, другая {{---}} нечетная. Тогда <tex>\mathrm{odd}(G\setminus B')\ = \mathrm{odd}(G\setminus B)\ - 1 </tex>. <br> | #: a) Одна компонента чётная, другая {{---}} нечетная. Тогда <tex>\mathrm{odd}(G\setminus B')\ = \mathrm{odd}(G\setminus B)\ - 1 </tex>. <br> | ||
| − | #: b) Обе компоненты чётные: <tex>\mathrm{odd}(G\setminus B')\ | + | #: b) Обе компоненты чётные: <tex>\mathrm{odd}(G\setminus B')\ = \mathrm{odd}(G\setminus B)\ + 1 </tex>. <br> |
| − | #: c) Обе компоненты нечётные: <tex>\mathrm{odd}(G\setminus B')\ | + | #: c) Обе компоненты нечётные: <tex>\mathrm{odd}(G\setminus B')\ = \mathrm{odd}(G\setminus B)\ - 1 </tex>. <br> |
#<tex>x</tex> смежна с одной компонентой связности графа <tex>G \setminus B</tex>. <br> | #<tex>x</tex> смежна с одной компонентой связности графа <tex>G \setminus B</tex>. <br> | ||
| − | #: a) Эта компонента чётная: <tex>\mathrm{odd}(G\setminus B')\ | + | #: a) Эта компонента чётная: <tex>\mathrm{odd}(G\setminus B')\ = \mathrm{odd}(G\setminus B)\ + 1 </tex>. <br> |
#: b) Эта компонента нечётная: <tex>\mathrm{odd}(G\setminus B')\ = \mathrm{odd}(G\setminus B)\ - 1 </tex>. <br> | #: b) Эта компонента нечётная: <tex>\mathrm{odd}(G\setminus B')\ = \mathrm{odd}(G\setminus B)\ - 1 </tex>. <br> | ||
# <tex>x</tex> не смежна ни с какой компонентой связности графа <tex>G \setminus B</tex>: <tex>\mathrm{odd}(G\setminus B')\ = \mathrm{odd}(G\setminus B)\ + 1 </tex>. <br> | # <tex>x</tex> не смежна ни с какой компонентой связности графа <tex>G \setminus B</tex>: <tex>\mathrm{odd}(G\setminus B')\ = \mathrm{odd}(G\setminus B)\ + 1 </tex>. <br> | ||
Версия 02:03, 15 декабря 2017
| Теорема: |
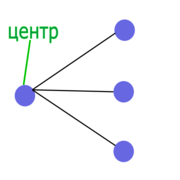
Пусть — минимальный по включению барьер графа , тогда каждая вершина — центр лапы в . |
| Доказательство: |
|
Предположим, что не является центром лапы. Тогда смежна не более чем с двумя компонентами связности графа .
Рассмотрев случаи, видим, что для любого из них выполнено: .
|
| Утверждение (D.P.Sumner, M.Las Vergnas, следствие из теоремы): |
Пусть — связный граф, не содержащий лапы, чётно. Тогда имеет совершенное паросочетание . |
|
Пусть — минимальный по включению барьер графа . Тогда, по предыдущей теореме имеем . |
См. также
- Декомпозиция Эдмондса-Галлаи
- Паросочетания: основные определения, теорема о максимальном паросочетании и дополняющих цепях
- Теорема Татта о существовании полного паросочетания
Источники информации
- Карпов Д. В. — Теория графов, стр 55