Пересечение всех максимальных по включению барьеров — различия между версиями
Scuuter (обсуждение | вклад) м (minor fixes_2.0) |
Scuuter (обсуждение | вклад) м (|B'| = |B| + k) |
||
| Строка 10: | Строка 10: | ||
|statement = Пересечение всех максимальных по включению барьеров графа <tex>G</tex> равно <tex>A(G)</tex>. | |statement = Пересечение всех максимальных по включению барьеров графа <tex>G</tex> равно <tex>A(G)</tex>. | ||
|proof = <tex>\supset</tex>.<br> | |proof = <tex>\supset</tex>.<br> | ||
| − | Пусть <tex>B</tex> {{---}} максимальный барьер, <tex>|A(G)\setminus B| = k > 0</tex>, <tex>B' = B \cup A(G)</tex>.<br> | + | Пусть <tex>B</tex> {{---}} максимальный барьер, <tex>|A(G)\setminus B| = k > 0</tex>, <tex>B' = B \cup A(G)</tex>, <tex>|B'| = |B| + k</tex>.<br> |
Докажем, что <tex>B'</tex> {{---}} барьер и получим противоречие. Для этого достаточно доказать, что <tex>\mathrm{odd}(G\setminus B')\ \geqslant \mathrm{odd}(G\setminus B)\ + k</tex>, ведь в таком случае <tex>\mathrm{odd}(G\setminus B')\ \geqslant \mathrm{def}(G)\ + |B| + k \Rightarrow \mathrm{odd}(G\setminus B')\ - |B'| \geqslant \mathrm{def}(G)</tex>. <br> | Докажем, что <tex>B'</tex> {{---}} барьер и получим противоречие. Для этого достаточно доказать, что <tex>\mathrm{odd}(G\setminus B')\ \geqslant \mathrm{odd}(G\setminus B)\ + k</tex>, ведь в таком случае <tex>\mathrm{odd}(G\setminus B')\ \geqslant \mathrm{def}(G)\ + |B| + k \Rightarrow \mathrm{odd}(G\setminus B')\ - |B'| \geqslant \mathrm{def}(G)</tex>. <br> | ||
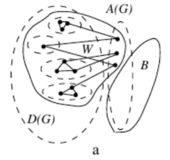
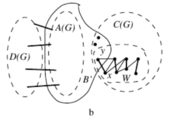
[[Файл: Max_barriers_a.png|170px|thumb|right|Рисунок 1]] | [[Файл: Max_barriers_a.png|170px|thumb|right|Рисунок 1]] | ||
Версия 21:41, 22 декабря 2017
| Теорема: |
Пересечение всех максимальных по включению барьеров графа равно . |
| Доказательство: |
|
. Пусть — компонента связности графа , содержащая вершин из (см. рисунок 1). |
См. также
- Декомпозиция Эдмондса-Галлаи
- Лапы и минимальные по включению барьеры в графе
- Паросочетания: основные определения, теорема о максимальном паросочетании и дополняющих цепях
- Теорема Татта о существовании полного паросочетания
Источники информации
- Карпов Д. В. — Теория графов, стр 54-55