Суффиксный автомат

Определение:

Суффиксный автомат (англ. suffix automaton, directed acyclic word graph) — минимальный ДКА, который принимает все суффиксы строки и только их.

Описание

Рассмотрим конечный алфавит [math]A[/math]. Пусть [math]A^*[/math] — набор слов в алфавите [math]A[/math]. Суффиксный автомат [math]\mathcal{A}[/math] — это набор [math]\langle Q, A, i, T, \delta \rangle[/math], где

• [math]Q[/math] — конечный набор состояний,
• [math]i[/math] — начальное состояние,
• [math]T[/math] — набор терминальных состояний,
• [math]\delta[/math] — функция перехода.

Для [math]q \in Q[/math] и [math]a \in A[/math], [math]\delta(q, a)[/math] определена, если состояние достижимо из [math]q[/math] переходом по символу [math]a[/math]. Функция перехода распространяется на слова и [math]\delta(q, x)[/math] обозначает, что если она существует, то состояние достигнуто после чтения слова [math]x[/math] из состояния [math]q[/math]. Автомат [math]\mathcal{A}[/math] распознает язык [math]\{x \in A^* : \delta(i, x) \in T \}[/math].

Суффиксный автомат [math]\mathcal{A}[/math] для строки [math]s[/math] представляет собой ациклический ориентированный граф, с начальной вершиной и множеством терминальных вершин, рёбра которого помечены символами [math]s[/math]:

• вершины этого графа — состояния автомата, а рёбра — переходы,
• каждый переход в автомате — ребро в графе, помеченное некоторым символом и все рёбра, исходящие из одной вершины имеют разные метки,
• одно из состояний называется начальным, из него достижимы все остальные состояния,
• одно или несколько состояний помечены как терминальные — если пройти от начального состояния до терминального по какому-либо пути и выписывать при этом символы на переходах, то получим один из суффиксов строки [math]s[/math].

Пример суффиксного автомата для строки [math]abbab[/math].

Определение:

Состояние [math]q[/math] принимает строку [math]s[/math], если существует путь из начального состояния в [math]q[/math], такой, что если последовательно выписать буквы на рёбрах на пути, получим строку [math]s[/math].

Определение:

Автомат принимает строку [math]s[/math], если её принимает хотя бы одно из финальных состояний.

Так как автомат детерминированный, то каждому пути соответствует строка.

Если две строки [math]a[/math] и [math]b[/math] принимаются одним состоянием [math]q[/math] произвольного автомата, то для любой строки [math]x[/math] строки [math]ax[/math] и [math]bx[/math] принимаются или не принимаются автоматом одновременно. Действительно, независимо от того, как мы пришли в состояние [math]q[/math], если мы пройдём из него по пути, соответствующему строке [math]x[/math], мы сможем точно сказать, в какое состояние мы попадём (в частности, будет ли оно финальным). Значит, любому состоянию [math]q[/math] соответствует множество строк [math]X_q[/math], которые переводят его в одно из конечных состояний.

Определение:

Множество [math]X_q[/math] называют правым контекстом состояния.

Правый контекст определен не только для состояния, но и для строк, которые оно принимает — правый контекст строк совпадает с правым контекстом состояния.

Утверждение:

Состояний в автомате не меньше, чем различных правых контекстов у подстрок строки, для которой он построен, причём в минимальном автомате достигается нижняя оценка.

[math]\triangleright[/math]

Допустим, что в автомате есть два состояния [math]q_1[/math] и [math]q_2[/math] такие что [math]X_{q_1} = X_{q_2}[/math]. Мы можем удалить состояние [math]q_2[/math] и перевести переходы, ведущие в него в состояние [math]q_1[/math]. Множество принимаемых строк от этого не изменится, следовательно, мы можем продолжать, пока количество состояний не будет равно числу попарно различных правых контекстов.

[math]\triangleleft[/math]

Таким образом, ДКА является минимальным тогда и только тогда, когда правые контексты всех его состояний попарно различны. В случае суффиксного автомата правый контекст [math]X_a[/math] строки [math]a[/math] взаимнооднозначно соответствует множеству правых позиций вхождений строки [math]a[/math] в строку [math]s[/math]. Таким образом, каждое состояние автомата принимает строки с одинаковым множеством правых позиций их вхождений и обратно, все строки с таким множеством позиций принимается этим состоянием.

Построение

Алгоритм

Определение:

Пусть длина самой короткой строки, которая принимается состоянием [math]q[/math] равно [math]k[/math], тогда суффиксная ссылка [math]\mathrm{link_q}[/math] будет вести из этого состояния в состояние, которое принимает эту же строку без первого символа.

Будем обозначать длину самой длинной строки, которая принимается состоянием [math]q[/math] как [math]\mathrm{len_q}[/math]. Длина самой короткой строки из [math]q[/math] в таком случае будет равна [math]\mathrm{len(link_q)} + 1[/math]. Суффиксный автомат может быть построен за линейное время (при константном размере алфавита) online-алгоритмом. Будем добавлять символы строки [math]s[/math] по одному, перестраивая при этом автомат. Изначально автомат состоит из одного состояния, для которого [math]\mathrm{len(0)} = 0[/math], а [math]\mathrm{link_0} = -1[/math].
Обозначим состояние [math]\mathrm{last}[/math], соответствующее текущей строке до добавления символа [math]c[/math] (изначально [math]\mathrm{last} = 0[/math]).
Создадим новое состояние [math]\mathrm{cur}[/math], [math]\mathrm{len(cur)} = \mathrm{len(last)} + 1[/math].
Рассмотрим все переходы из [math]\mathrm{last}[/math] по текущему символу [math]c[/math]. Если перехода нет, то добавляем переход в [math]\mathrm{cur}[/math], переходим по суффиксной ссылке и повторяем процедуру снова. Если переход существует, то остановимся и обозначим текущее состояние за [math]p[/math]. Если перехода не нашлось и по суффиксным ссылкам мы дошли до фиктивного состояния (на которое указывает [math]\mathrm{link_0}[/math]), то [math]\mathrm{link_{cur}} = 0[/math].
Допустим, что мы остановились в состоянии [math]p[/math], из которого существует переход с символом [math]c[/math]. Обозначим состояние, куда ведёт переход, через [math]q[/math]. Рассмотрим два случая:

1. Если [math]\mathrm{len(p)} + 1 = \mathrm{len(q)}[/math], то [math]\mathrm{link(q)} = \mathrm{cur}[/math].
   
2. В противном случае, создадим новое состояние [math]\mathrm{new}[/math], скопируем в него [math]q[/math] вместе с суффиксными ссылками и переходами. [math]\mathrm{len(new)}[/math] присвоим значение [math]\mathrm{len(p)} + 1[/math]. Перенаправим суффиксную ссылку из [math]q[/math] в [math]\mathrm{new}[/math] и добавим ссылку из [math]\mathrm{cur}[/math] в [math]\mathrm{new}[/math]. Пройдём по всем суффиксным ссылкам из состояния [math]p[/math] и все переходы в состояние [math]q[/math] по символу [math]c[/math] перенаправим в [math]\mathrm{new}[/math].

Обновим значение [math]\mathrm{last} = \mathrm{cur}[/math].

Пример построения

Изображение	Описание
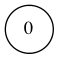
	Изначально автомат состоит из одного начального состояния. [math]\mathrm{last} = 0, \mathrm{len(0)} = 0[/math]
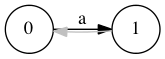
	Добавляем символ [math]a[/math]. Создаем состояние [math]1[/math]. Переходов из начального состояния по символу [math]a[/math] нет, перейти по суффиксным ссылкам некуда, значит добавим суффиксную ссылку [math]\mathrm{link_{1}} = 0[/math]. [math]\mathrm{last} = 1, \mathrm{len(1)} = 1[/math]
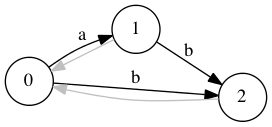
	Добавляем символ [math]b[/math]. Создаем состояние [math]2[/math]. Добавим переход из [math]1[/math], откатимся по суффиксной ссылке и добавим переход из [math]0[/math]. Добавим суффиксную ссылку [math]\mathrm{link_{2}} = 0[/math]. [math]\mathrm{last} = 2, \mathrm{len(2)} = 2[/math]
	Аналогично добавим символ [math]c[/math] и обновим автомат. [math]\mathrm{last} = 3, \mathrm{len(3)} = 3[/math]
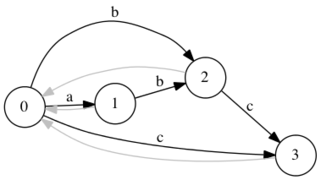
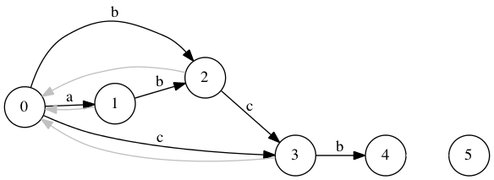
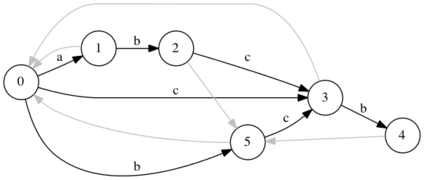
	Добавляем символ [math]b[/math]. Добавим переход из [math]3[/math] и перейдем по суффиксной ссылке в начальное состояние. Из состояния [math]0[/math] существует переход по символу [math]b[/math]
	Рассмотрим состояние [math]2[/math], куда существует переход. Имеем [math]\mathrm{len(0)} + 1 \neq \mathrm{len(2)}[/math]. Создаем новое состояние [math]5[/math]. Копируем в него все суффиксные ссылки и переходы из [math]2[/math] и присвоим [math]\mathrm{len(5)} = \mathrm{len(0)} + 1 = 1[/math]. Перенаправим суффиксную ссылку из [math]2[/math] в [math]5[/math] и добавим ссылку из [math]4[/math] в [math]5[/math]. Перенаправим переход [math]0 \rightarrow 2[/math] в состояние [math]5[/math].
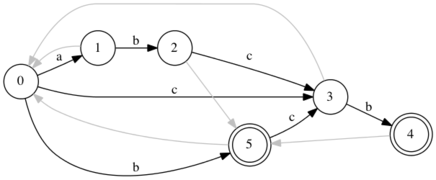
	Построение автомата завершено. Чтобы пометить терминальные вершины, найдём состояние, которое принимает строку [math]abcb[/math] и пройдём по суффиксным ссылкам, помечая все посещенные состояния терминальными.

Реализация

В приведённой ниже реализации используются следующие переменные:

• [math]\mathrm{edges[]}[/math] — массив отображений (ключ — символ, значение — номер состояния) с переходами,
• [math]\mathrm{link[]}[/math] — массив суффиксных ссылок,
• [math]\mathrm{len[]}[/math] — массив длин строк,
• [math]\mathrm{newState()}[/math] — функция, которая создаёт новое состояние и возвращает его номер,
• [math]\mathrm{clone()}[/math] — функция, которая копирует состояние и возвращает номер нового состояния,
• [math]\mathrm{last}[/math] — последнее состояние.

func addChar(c : char):
    int cur = newState()                                       // создаём новое состояние и получаем его номер 

    int p = last
    while p >= 0 and edges[p].find(c) == null
        edges[p][c] = cur
        p = link[p]

    if p != -1
        int q = edges[p][c]
        if len[p] + 1 == len[q]
            link[cur] = q
        else
            int new = clone(q)                                // скопируем состояние [math]q[/math] и получим номер нового состояния
            len[new] = len[p] + 1
            link[q] = link[cur] = new
            while p >= 0 and edges[p][c] == q
                edges[p][c] = new
                p = link[p]
    last = cur

Применение

Проверка вхождения строки

Задача:

Даны строки [math]s[/math] и [math]p[/math]. Требуется проверить, является ли строка [math]p[/math] подстрокой [math]s[/math].

Построим суффиксный автомат для строки [math]s[/math].
Пусть текущее состояние — [math]\mathrm{cur}[/math], изначально равно [math]0[/math] (начальному состоянию).
Будем по очереди обрабатывать символы строки [math]p[/math]. Если из состояния [math]\mathrm{cur}[/math] есть переход в по текущему символу, то перейдем в новое состояние и повторим процедуру. Если перехода не существует, то [math]p[/math] не является подстрокой [math]s[/math]. Если успешно обработали все символы [math]p[/math], то она является подстрокой [math]s[/math].
Асимптотика — построение суфавтомата за [math]O(|s|)[/math], проверка за [math]O(|p|)[/math].

Позиция первого вхождения строки

Задача:

Даны строки [math]s[/math] и [math]p[/math]. Требуется найти позицию первого вхождения строки [math]p[/math] в [math]s[/math].

Построим суффиксный автомат для строки [math]s[/math].
В процессе построения для каждого состояния [math]q[/math] будем хранить значение [math]\mathrm{first(q)}[/math] — позицию окончания первого вхождения строки. Поддерживать позицию [math]\mathrm{first}[/math] можно следующим образом: при добавлении нового состояния [math]\mathrm{first(cur)} = \mathrm{len(cur)} - 1[/math], а при клонировании вершины [math]\mathrm{first(new)} = \mathrm{first(q)}[/math].
Для поиска вхождения обойдём автомат, как в предыдущей задаче. Пусть состояние [math]p'[/math] в автомате соответствует строке [math]p[/math]. Тогда ответ на задачу [math]\mathrm{first(p')} - |p| + 1[/math].
Асимптотика — построение суфавтомата за [math]O(|s|)[/math], проверка за [math]O(|p|)[/math].

Количество различных подстрок

Задача:

Дана строка [math]s[/math]. Найти количество различных подстрок строки [math]s[/math].

Построим суффиксный автомат для строки [math]s[/math].
Каждой подстроке в суффиксном автомате соответствует путь, тогда ответ на задачу — количество различных путей из начальной вершины. Так как суфавтомат представляет собой ациклический граф, мы можем найти количество путей в графе методом динамического программирования.

Наибольшая общая подстрока двух строк

Задача:

Даны строки [math]s[/math] и [math]t[/math]. Требуется найти наибольшую общую подстроку двух строк.

Построим суффиксный автомат для строки [math]s[/math].
Пройдём по строке [math]t[/math] и для текущего символа будем искать длину наибольшей общей подстроки, которая заканчивается в текущей позиции. Для этого будем поддерживать [math]v[/math] — текущее состояние и [math]l[/math] — текущую длину совпадающей части.
Изначально [math]v = 0[/math], [math]l = 0[/math] — совпадение пустое. Рассматриваем текущий символ [math]t_i[/math]. Если в автомате существует переход из текущего состояния по данному символу, то перейдем в новое состояние и увеличим длину [math]l[/math] на [math]1[/math].
Если перехода не существует, то попробуем минимально уменьшить длину совпадающей подстроки: перейдем по суффиксной ссылке из [math]v[/math] в новое состояние и примем [math]l = \mathrm{len(v)}[/math]. Повторим операцию до тех пор, пока не найдём переход. Если по суффиксным ссылкам мы дошли до состояния, в которое ведёт суффиксная ссылка начальной вершины, то это значит, что символа [math]t_i[/math] нет в строке [math]s[/math]. В таком случае примем [math]v = l = 0[/math], после чего перейдем к следующему символу строки [math]t[/math].
Длиной наибольшей общей подстроки будет [math]\mathrm{maxLen}[/math] — максимум из всех значений [math]l[/math], полученных в ходе работы алгоритма. Тогда ответом на задачу будет являться подстрока [math]t[(\mathrm{maxPos} - \mathrm{maxLen} + 1) .. \mathrm{maxPos}][/math], где [math]\mathrm{maxPos}[/math] — позиция, в которой достигнут максимум.

Сравнение с другими суффиксными структурами

Пусть [math]s[/math] — строка, для которой строим соответствующую структуру, [math]n = |s|[/math], [math]\Sigma[/math] — алфавит.

	Время работы	Память
Суффиксный бор	[math]O(n ^ 2)[/math]	[math]O(n^2 + n |\Sigma|)[/math]
Сжатое суффиксное дерево	[math]O(n \log{|\Sigma|})[/math]	[math]O(n |\Sigma|)[/math]
Суффиксный массив	[math]O((n + |\Sigma|) \log{n})[/math]	[math]O(n + |\Sigma|)[/math]
Суффиксный автомат	[math]O(n \log{|\Sigma|})[/math]	[math]O(n)[/math]

См. также

• Автомат для поиска образца в тексте
• Алгоритм Ахо-Корасик
• Поиск наибольшей общей подстроки двух строк с использованием хеширования

Источники информации

• Maxime Crochemore, Christophe Hancart, Thierry Lecroq — Algorithms on Strings
• А. Кульков — Лекция по суффиксным структурам
• MAXimal :: algo :: Суффиксный автомат