Автоматы в современном мире

Реализация регулярных выражений в современных языках

В настоящее время используется несколько различных подходов к реализации регулярных выражений. Всегда можно довольно просто построить НКА. Но после построения есть несколько вариантов:

1. Можно конвертировать его в детерминированный конечный автомат.
2. Можно идти по каждому из возможных путей, а в случае неудачи возвращаться назад и пробовать другой.
3. Можно идти по автомату одновременно по всем возможным состояниям.
4. Можно конвертировать НКА в ДКА лениво (на лету).

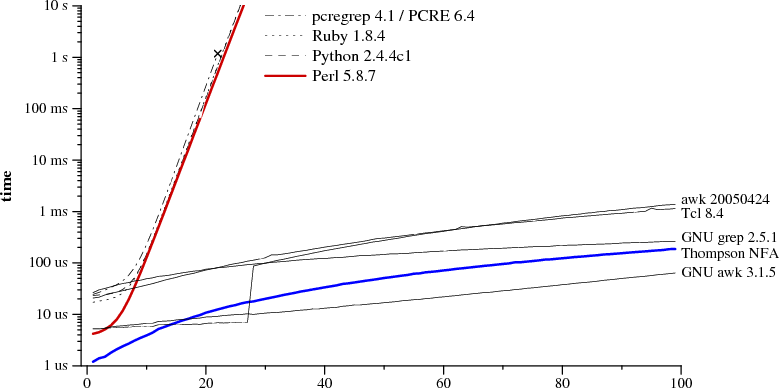
Следующее изображение наглядно показывает, что можно выделить более менее два основных подхода к реализации, давайте же разберемся почему так получилось.

regular expression and text size n [math]a?^na^n[/math] matching [math]a^n[/math]

Это произошло из-за того, что обычного функционала регулярных выражений зачастую недостаточно, не хватает выразительной мощности. В языках PCRE, Ruby, Python, Perl добавили поддержку обратных ссылок (англ. back reference). Она позволяет связывать ранее найденное сгруппированное выражение в скобках с числом от [math]1[/math] до [math]9[/math]. Например: [math]\mathtt{(cat|dog)\backslash1}[/math] найдет [math]\mathtt{catcat}[/math] или [math]\mathtt{dogdog}[/math], но никак не [math]\mathtt{catdog}[/math] или [math]\mathtt{dogcat}[/math]. Интересно, что с добавлением обратных ссылок регулярные выражения перестаю относиться к классу регулярных языков. К сожалению, лучшая реализация требует экспоненциального времени работы. Приведенная на графике синяя кривая является реализацией построения НКА по регулярному выражению написанная на C, занимающая чуть меньше, чем [math]400[/math] строк и описанная в данной статье.

Построение НКА

Для построения автомата нам нужно построить отдельно части НКА для каждой части выражения, финальным шагом будет соединение всего автомата вместе. Для примера напишем программу на C, представим НКА как связанный список структур состояний [math]\mathrm{state}[/math]

struct state
   int c;
   state *out;
   state *out1;
   int lastlist;

Каждый [math]\mathrm{state}[/math] представляет один из фрагментов НКА, зависящий от символа c. Данная реализация будет поддерживать постфиксную нотацию регулярного выражения. Допустим у нас есть функция [math]\mathrm{re2post}[/math], которая переписывает инфиксную форму регулярного выражения [math]``a(bb)+a"[/math] в эквивалентную постфиксную вида [math]``abb.+.a."[/math] ([math].[/math] используется в качестве разделителя). По мере сканирования постфиксного выражения, будем поддерживать стек вычисленных НКА фрагментов. Символы добавляют новый НКА фрагмент в стек, а операторы вынимают фрагменты и добавляют новые. Каждый фрагмент определяется стартовым состояние и исходящей стрелкой:

struct frag
  state *start;
  ptrList *out;

[math]\mathrm{start}[/math] указывает на стартовое состояние фрагмента, а [math]\mathrm{out}[/math] — лист указателей на [math]\mathrm{state*}[/math] указатели, которые ещё не соединены. Некоторые полезные функции для управления списком указателей:

fun *list1(state **outp): ptrList
fun *append(ptrList *l1, ptrList *l2): ptrList
fun patch(ptrList *l, state *s):

[math]\mathrm{list1}[/math] создает новый список указателей состоящий из одного указателя [math]\mathrm{outp}[/math]. [math]\mathrm{append}[/math] конкатенирует два списка указателей, возвращая результат. [math]\mathrm{patch}[/math] связывает повисшую стрелку в списке [math]\mathrm{l}[/math] с состоянием [math]\mathrm{s}[/math]. Используя данные примитивы и стек фрагментов можно реализовать построение НКА.

fun post2nfa(char *postfix):state*
   char *p;
   frag stack[1000], *stackp, e1, e2, e;
   state *s;
   #define push(s) *stackp++ = s
   #define pop()   *--stackp
   stackp = stack;
   for (p = postfix; *p; p++)
     switch(*p)
         default: // символ
           s = state(*p, NULL, NULL)
           push(frag(s, list1(&s->out))
           break
         case '.': // конкатенация
           e2 = pop()
           e1 = pop()
           patch(e1.out, e2.start)
           push(frag(e1.start, e2.out))
           break
         case '|': // альтернатива
           e2 = pop()
           e1 = pop()
           s = state(Split, e1.start, e2.start)
           push(frag(s, append(e1.out, e2.out)))
           break
         case '?': // ноль или один
           e = pop()
           s = state(Split, e.start, NULL)
           push(frag(s, append(e.out, list1(&s->out1))))
           break
         case '*': // ноль или больше
           e = pop()
           s = state(Split, e.start, NULL)
           patch(e.out, s)
           push(frag(s, list1(&s->out1)))
           break
         case '+': // один или больше
           e = pop()
           s = state(Split, e.start, NULL)
           patch(e.out, s)
           push(frag(e.start, list1(&s->out1)))
           break
   e = pop()
   patch(e.out, matchState);
   return e.start;

Теперь когда мы построили НКА, нужно научиться ходить по нему. Будем сохранять посещенные состояния в массиве.

struct List:
  state **s
  int n

Обход будет использовать два списка: [math]\mathrm{cList}[/math] набор состояний, в которых уже находится, и [math]\mathrm{nList}[/math] набор состояний в которых НКА будет после обработки текущего символа. Цикл исполнения инициализирует [math]\mathrm{cList}[/math] стартовым состоянием и пошагово проходит.

int match(state *start, char *s)
  List *cList, *nList, *t;
  cList = startList(start, &l1);
  nList = &l2;
  for ( ; *s, s++) {
    step(cList, *s, nList);
    t = cList; cList = nList; nList = t;
  return isMatch(cList);

Чтобы избежать преаллокаций на каждой итерации цикла, [math]\mathrm{match}[/math] использует два преаллоцированных списка [math]\mathrm{l1}[/math] и [math]\mathrm{l2}[/math] как [math]\mathrm{cList}[/math] и [math]\mathrm{nList}[/math], и меняет их на каждом шаге.

Если список последних вершин содержит терминальную вершину, то строка распознана.

int isMatch(List *l)
  int i;
  for (i = 0; i < l->n; i++)
    if (l->s[i] == matchState)
      return 1;
  return 0;

[math]\mathrm{addState}[/math] добавляет состояние в список, но только если их ещё не было в нем.

void addState(List *l, state *s)
  if (s == NULL || s->lastlist == listid)
    return;
  s->lastlist = listid;
  if(s->c == split) {
    addState(l, s->out);
    addState(l, s->out1);
    return;
  l->s[l->n++] = s;

[math]\mathrm{startList}[/math] создает начальный список состояний и добавляет туда стартовое состояние.

List* startList(state *s, List *l)
  listid++;
  l->n = 0;
  addState(l, s);
  return l;

[math]\mathrm{step}[/math] вычисляет по символу, использую список текущих состояний [math]\mathrm{cList}[/math] следующий список [math]\mathrm{nList}[/math].

void step(List *client, int c, List *nList)
  int i;
  state *s;
  listid++;
  nList->n = 0;
  for (i = 0; i < cList->n; i++)
    s = cList->s[i];
    if (s->c == c)
      addState(nList, s->out);

Дополнительные возможности регулярных выражений

Символьные классы

Набор символов в квадратных скобках [math][ ][/math] именуется символьным классом и позволяет указать интерпретатору регулярных выражений, что на данном месте в строке может стоять один из перечисленных символов. Можно указывать диапазоны [math]\mathrm{[0-9]}, \mathrm{[a-z]}[/math], а также существуют дополнительные символьные классы [math]\mathtt{[[:upper:]]}, \mathtt{[[:word:]]}[/math].

Квантификация.

Позволяет установить точное соответствие повторов равное числу [math]n[/math] — [math]{n};[/math] [math]{n,m}[/math] — не меньше чем [math]n[/math], и не больше чем [math]m[/math]. [math]{n,}[/math] — [math]n[/math] и больше. Можно найти эквиваленты символам [math]*, +, ?[/math]. С помощью символов [math]\{ \}[/math]

[math]?[/math]	[math]{0,1}[/math]
[math]+[/math]	[math]{1,}[/math]
[math]*[/math]	[math]\{ \}[/math]

Позиция внутри строки

Следующие символы позволяют с позиционировать регулярное выражение относительно элементов текста: начала и конца строки, границ слова.

Представление	Позиция
[math] \wedge [/math]	Начало текста
[math]$[/math]	Конец текста
[math]\backslash b[/math]	Граница слова
[math]\backslash G[/math]	Предыдущий успешный поиск

Жадная и ленивая квантификация

В некоторых реализациях квантификаторам в регулярных выражениях соответствует максимально длинная строка из возможных (квантификаторы являются жадными, англ. greedy). Это может оказаться значительной проблемой. Например, часто ожидают, что выражение [math](\lt .*\gt )[/math] найдёт в тексте теги HTML. Однако если в тексте есть более одного HTML-тега, то этому выражению соответствует целиком строка, содержащая множество тегов.

Жадный	Ленивый
[math]*[/math]	[math]*?[/math]
[math]+[/math]	[math]+?[/math]
[math]\{n,\}[/math]	[math]\{n,\}?[/math]

Эту проблему можно решить двумя способами.

Учитывать символы, не соответствующие желаемому образцу ( [math]\lt [^\gt ]*\gt [/math] для вышеописанного случая). Определить квантификатор как нежадный (ленивый, англ. lazy) — большинство реализаций позволяют это сделать, добавив после него знак вопроса.

Ревнивая квантификация (Сверхжадная)

В отличие от обычной (жадной) квантификации, ревнивая (англ. possessive) квантификация не только старается найти максимально длинный вариант, но ещё и не позволяет алгоритму возвращаться к предыдущим шагам поиска для того, чтобы найти возможные соответствия для оставшейся части регулярного выражения.

Использование квантификаторов увеличивает скорость поиска, особенно в тех случаях, когда строка не соответствует регулярному выражению. Кроме того, ревнивые квантификаторы могут быть использованы для исключения нежелательных совпадений.

Жадный	Ревнивый
[math]*[/math]	[math]*+[/math]
[math]?[/math]	[math]?+[/math]
[math]+[/math]	[math]++[/math]
[math]\{n,\}[/math]	[math]\{n,\}+[/math]

Несколько полезных оптимизаций на примере Haskell

Gabriel Gonzalez реализовал алгоритм Томпсона на языке Haskell. В первоначальном варианте это алгоритм получился в 480 раз медленнее, чем grep на том же тесте, чтобы улучшить результат он предпринял ряд оптимизаций:

• вместо Set Int использовал Integer, а также использовал битовые операции, в результате производительность выросла в 5 раз
• использовал Word вместо Integer, ещё в 8 раз быстрее
• а также использовал ByteString оптимизации, что увеличило производительность ещё 3 раза.

В итоге его реализация оказалась всего в 4 раза медленнее grep. Но это не предел, у него получилось реализовать параллельный конечный автомат и сделать свою реализацию в 1.5 раза быстрее, чем grep.

ReDoS (regular expression denial of service)

Интересно, что злоумышленники научились атаковать системы используя то, что некоторые алгоритмы имеют экспоненциальную сложность. В регулярных выражениях использующих обратную связь есть несколько вариантов:

• использовать повторение [math](``+",``*")[/math] для достаточно сложных подвыражений;
• сделать так, чтобы повторяющиеся подвыражения были суффиксами валидного совпадения.

Примеры вредоносных регулярных выражений:

• [math](a+)+[/math]
• [math]([a-zA-Z]+)*[/math]
• [math](a|aa)+[/math]
• [math](a|a?)+[/math]
• [math](.*a)\{11,\}[/math]

Все эти выражения чувствительны к входной строке [math]aaaaaaaaaaaaaaaaaaaaaaaaaa[/math]. Также вредоносные регулярные выражения были обнаружены в онлайн репозиториях.

1. RegExLib, id=1757 (email validation) - выделенная часть является вредоносной
   ^([a-zA-Z0-9])(([\-.]|[_]+)?([a-zA-Z0-9]+))*(@){1}[a-z0-9]+[.]{1}(([a-z]{2,3})|([a-z]{2,3}[.]{1}[a-z]{2,3}))$
2. OWASP Validation Regex Repository, Java Classname - выделенная часть является вредоносной
   ^(([a-z])+.)+[A-Z]([a-z])+$

Эти два примера также чувствительны к входной строке [math]aaaaaaaaaaaaaaaaaaaaaaaa[/math].

См. также

• Регулярные языки: два определения и их эквивалентность
• Недетерминированные конечные автоматы
• Детерминированные конечные автоматы
• Построение по НКА эквивалентного ДКА, алгоритм Томпсона

Источники информации

• Regular Expression Matching Can Be Simple And Fast
• ReDos
• Data-Parallel Finite-state Machines