Левосторонние красно-чёрные деревья

Определение:

Left-leaning Red-Black Trees — модификация красно-черных деревьев, имеющая ряд преимуществ на классической структурой. Разработана Робертом Соджевиском в 2008 году.

Преимущества

• необходимо менее 80 строчек кода для реализации структуры
• более быстрая вставка, удаление элементов
• простота

Вращения

Чтобы поддерживать красно-черные двоичное деревья поиска необходимо соблюдать следующие инвариантные свойства при вставке и удалении:

• Ни один обход от корня до листьев дерева не содержит двух последовательных красных узлов.
• Количество черных узлов на каждом таком пути одинаково.

Из этих инвариантов следует, что длина каждого пути от корня до листьев в красно-черном дереве с [math]N[/math] узлами не превышает [math]2 \cdot \log(N)[/math] .

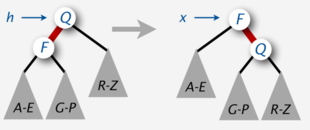
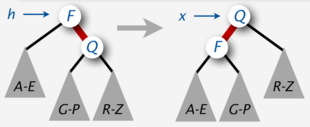
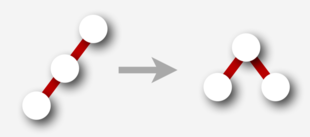
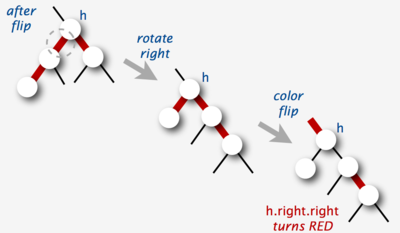
Основные операции, используемые алгоритмами сбалансированного дерева для поддержания баланса при вставке и удалении, называются вращениями. Эти операции трансформируют [math]3[/math]-узел,левый потомок которого окрашен в красный, в [math]3[/math]-узел, правый потомок которого окрашен в красный и наоборот. Вращения сохраняют два указанных выше инварианта, не изменяют поддеревья узла.

Псевокод

Rotate Right

  Node rotateRight( h : Node) :
      x = h.left
      h.left= x.right
      x.right= h
      x.color = h.color
      h.color = RED
   return x

Rotate Left

  Node rotateLeft( h : Node) :
      x = h.right
      h.right = x.left
      x.left = h
      x.color = h.color
      h.color = RED
  return x

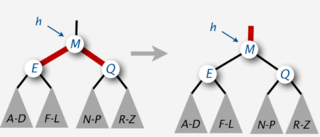
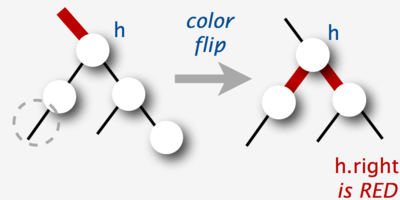
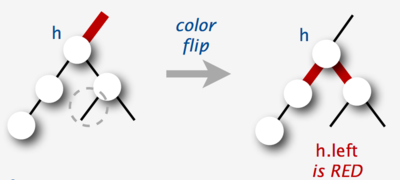
Переворот цветов

В красно-черных деревьях используется такая операция как Переворот цветов [math](flip color)[/math] , которая инвертирует цвет узла и двух его детей. Она не изменяет количество черных узлов при любом обходе от корня до листьев дерева, но может привести к появлению двух последовательных красных узлов.

Color Flip

 void flipColors( h : Node h) :
      h.color = ! h.color
      h.left.color =  ! h.left.color
      h.right.color = [math] ![/math] h.right.color

Вставка

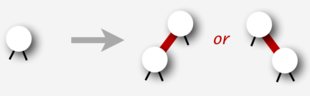
Вставка в LLRB базируется на [math]4[/math] простых операциях:

• Вставка нового узла к листу дерева:

Вставка нового узла

 if (h == null)
      return new Node(key, value, RED);

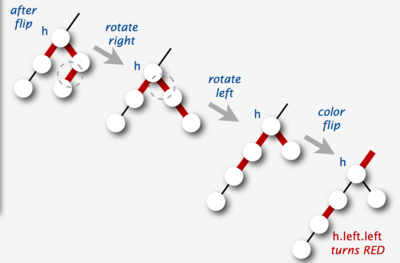
• Расщепление узла с [math]4[/math]-я потомками:

Расщепление узла

 if (isRed(h.left) && isRed(h.right))
     colorFlip(h);

• Принудительное вращение влево:

Принудительное вращение

 if (isRed(h.right))
     h = rotateLeft(h);

• Балансировка узла с [math]4[/math]-я потомками:

Балансировка

 if (isRed(h.left) && isRed(h.left.left))
     h = rotateRight(h);
  

Псевдокод

 void insert( key : Key, value : Value ): 
        root = insert(root, key, value)
        root.color = BLACK

 Node insert( h : Node, key : Key, value : Value):
     //Вставка нового узла к листу дерева
     if h == null     
         return new Node(key, value)
     //Расщепление узла с [math]4[/math]-я потомками
     if isRed(h.left) && isRed(h.right)
         colorFlip(h)
     //Стандартная вставка в дереве поиска
     int cmp = key.compareTo(h.key) 
     if  cmp == 0
         h.val = value
     else 
         if cmp < 0 
             h.left = insert(h.left, key, value)  
         else 
             h.right = insert(h.right, key, value)
         //Принудительное вращение влево
         if isRed(h.right) && !isRed(h.left)    
             h = rotateLeft(h)
         ////Балансировка узла с [math]4[/math]-я потомками
         if isRed(h.left) && isRed(h.left.left)
             h = rotateRight(h)
 return h

Поиск

Псевдокод

Value search(key : Key):
    Node x = root
    while (x != null)
      int cmp = key.compareTo(x.key)
      if (cmp == 0)
          return x.val
      else
          if (cmp < 0)
              x = x.left
      else 
          if (cmp > 0) 
              x = x.right
return null

Удаление

Исправление правых красных связей

• Использование [math]flipColor[/math] и [math]rotate[/math] сохраняют баланс черной связи.
• После удаления необходимо исправить правые красные связи и устранить узлы с [math]4-[/math]я потомками

     //Исправление правых красных связей
  Node fixUp(h : Node){
      if (isRed(h.right))
          h = rotateLeft(h);
     //Вращение [math]red-red[/math] пары
      if (isRed(h.left) && isRed(h.left.left))
          h = rotateRight(h);
     //Балансировка узла с [math]4[/math]-я потомками
      if (isRed(h.left) && isRed(h.right))
          colorFlip(h);
  return h; 
 }

Удаление максимума

• Спускаемся вниз по правому краю дерева.
• Если поиск заканчивается на узле с [math]4[/math]-мя или [math]5[/math]-ю потомками, просто удаляем узел.

Узлы до и после удаления

• Удаление узла с [math]2[/math]-я потомками разрушает баланс

Соответственно спускаясь вниз по дереву необходимо поддерживать следующий инвариант : количество потомков узла не должно быть ровно [math]2[/math]-м.

Будем поддерживать инвариант : Для любого узла либо сам узел, либо правый предок узла красный. Будем придерживаться тактики , что удалять лист легче, чем внутренний узел.

Заметим, что если правый потомок вершины и правый потомок правого потомка вершины черные, необходимо переместить левую красную ссылку вправо для сохранения инварианта.

Перемещение красной ссылки. Простой случай

Перемещение красной ссылки. Сложный случай

Псевдокод

void deleteMax()
    root = deleteMax(root);
    root.color = BLACK;

Node moveRedLeft(h : Node)
    colorFlip(h);
    if (isRed(h.right.left)
        h.right = rotateRight(h.right);
        h = rotateLeft(h);
        colorFlip(h);
return h;   

Node deleteMax(h : Node)
    if (isRed(h.left)) 
    //вращаем все 3-вершины вправо
        h = rotateRight(h);
    //поддерживаем инвариант (h должен быть красным)
    if (h.right == null)   
        return null;
    //заимствуем у брата если необходимо
    if (!isRed(h.right) && !isRed(h.right.left)) 
        h = moveRedRight(h);
    // опускаемся на один уровень глубже 
    h.left = deleteMax(h.left); 
    //исправление правых красных ссылок и 4-вершин на пути вверх
    return fixUp(h);

Удаление минимума

Поддерживаем инвариант: вершина или левый ребенок вершины красный.

Заметим, что если левый потомок вершины и левый потомок левого потомка вершины черные, необходимо переместить красную ссылку для сохранения инварианта.

Перемещение красной ссылки. Простой случай

Перемещение красной ссылки. Сложный случай

Псевдокод

Node moveRedLeft(h : Node)
    colorFlip(h);
    if (isRed(h.right.left))
        h.right = rotateRight(h.right);
        h = rotateLeft(h);
        colorFlip(h);
return h;

void deleteMin()
    root = deleteMin(root);
    root.color = BLACK;

Node deleteMin(h : Node)
   //удаляем узел на нижнем уровне(h должен быть красным по инварианту)
    if (h.left == null)    
        return null;
    //Если необходимо, пропушим  красную ссылку вниз
    if  !isRed(h.left) &&  !isRed(h.left.left)
         h = moveRedLeft(h);
    //опускаемся на уровень ниже
    h.left = deleteMin(h.left);
return fixUp(h);