Паросочетания: основные определения, теорема о максимальном паросочетании и дополняющих цепях

Паросочетание в двудольном графе

Определение:

Паросочетание (англ. matсhing) [math]M[/math] в двудольном графе — произвольное множество рёбер двудольного графа, такое что никакие два ребра не имеют общей вершины.

Определение:

Вершины двудольного графа, инцидентные рёбрам паросочетания [math]M[/math], называются покрытыми (англ. matched), а неинцидентные — свободными (англ. unmatched).

Определение:

Числом рёберного покрытия (англ. edge covering number) называется размер минимального рёберного покрытии графа [math]G[/math] и обозначается через [math]\rho(G)[/math].

Определение:

Число рёбер в наибольшем паросочетании графа [math]G[/math] называется числом паросочетания (англ. matching number).

Определение:

Максимальное паросочетание (англ. maximal matching) — это такое паросочетание [math]M[/math] в графе [math]G[/math], которое не содержится ни в каком другом паросочетании этого графа, то есть к нему невозможно добавить ни одно ребро, которое бы являлось несмежным ко всем рёбрам паросочетания.

Другими словами, паросочетание [math]M[/math] графа [math]G[/math] является максимальным, если любое ребро в [math]G[/math] имеет непустое пересечение по крайней мере с одним ребром из [math]M[/math].

Определение:

Паросочетание [math]M[/math] графа [math]G[/math] называется совершенным (или полным) (англ. perfect matching), если оно покрывает все вершины графа.

Определение:

Чередующаяся цепь (англ. alternating path) — путь в двудольном графе, для любых двух соседних рёбер которого верно, что одно из них принадлежит паросочетанию [math]M[/math], а другое нет.

Определение:

Дополняющая цепь (или увеличивающая цепь) (англ. augmenting path) — чередующаяся цепь, у которой оба конца свободны.

Определение:

Уменьшающая цепь (англ. reduce path) — чередующаяся цепь, у которой оба конца покрыты.

Определение:

Сбалансированная цепь (англ. balanced path) — чередующаяся цепь, у которой один конец свободен, а другой покрыт.

Свойства

В любом графе без изолированных вершин, число паросочетания и число рёберного покрытия в сумме дают число вершин. Если существует совершенное паросочетание, то оба числа равны [math]|V|/2[/math].

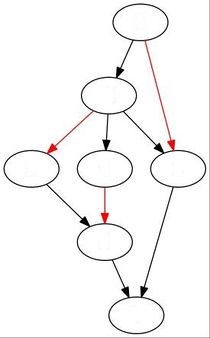
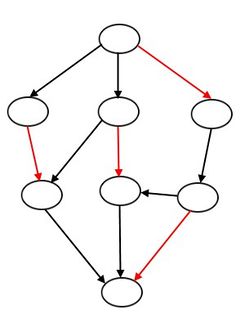
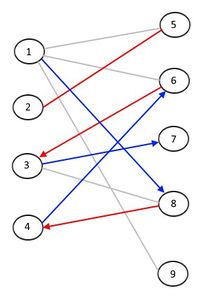
Пример максимального и полного паросочетания, чередующейся цепи

красные рёбра являются рёбрами максимального паросочетания

красные рёбра являются рёбрами полного паросочетания.

Пусть красные рёбра принадлежат паросочетанию [math]M[/math], а синие не принадлежат, тогда чередующаяся цепь: [math]1-8-4-6-3-7[/math]

Теорема о максимальном паросочетании и дополняющих цепях

Теорема:

Паросочетание [math]M[/math] в двудольном графе [math]G[/math] является максимальным тогда и только тогда, когда в [math]G[/math] нет дополняющей цепи.

Доказательство:

[math]\triangleright[/math]

[math]\Rightarrow[/math] Пусть в двудольном графе [math]G[/math] с максимальным паросочетанием [math]M[/math] существует дополняющая цепь. Тогда пройдя по ней и заменив вдоль неё все рёбра, входящие в паросочетание, на невходящие и наоборот, мы получим большее паросочетание. То есть [math]M[/math] не являлось максимальным. Противоречие. [math]\Leftarrow[/math] Рассмотрим паросочетание [math]M[/math] в графе [math]G[/math] и предположим, что [math]M[/math] — не наибольшее. Докажем, что тогда имеется увеличивающая цепь относительно [math]M[/math]. Пусть [math]M'[/math] — другое паросочетание и [math]|M'|\gt |M|[/math]. Рассмотрим подграф [math]H[/math] графа [math]G[/math], образованный теми рёбрами, которые входят в одно и только в одно из паросочетаний [math]M[/math], [math]M'[/math]. Иначе говоря, множеством рёбер графа [math]H[/math] является симметрическая разность [math]M\oplus M'[/math]. В графе [math]H[/math] каждая вершина инцидентна не более чем двум рёбрам (одному из [math]M[/math] и одному из [math]M'[/math] ), т.е. имеет степень не более двух. В таком графе каждая компонента связности — путь или цикл. В каждом из этих путей и циклов чередуются рёбра из [math]M[/math] и [math]M'[/math]. Так как [math]|M'|\gt |M|[/math], имеется компонента, в которой рёбер из [math]M'[/math] содержится больше, чем рёбер из [math]M[/math]. Это может быть только путь, у которого оба концевых ребра принадлежат [math]M'[/math]. Заметим, что относительно [math]M[/math] этот путь является увеличивающей (дополняющей) цепью.

[math]\triangleleft[/math]

См. также

• Теорема Холла
• Связь максимального паросочетания и минимального вершинного покрытия в двудольных графах
• Связь вершинного покрытия и независимого множества

Источники информации

• Wikipedia — Matching
• Википедия — Паросочетание
• Асанов М. О., Баранский В. А., Расин В. В. — Дискретная математика: Графы, матроиды, алгоритмы. стр. 227-232 ISBN 978-5-8114-1068-2