Совпадение множества языков МП-автоматов и контекстно-свободных языков

Эта статья находится в разработке!

Эквивалентность МП-автоматов и КС-языков

Далее будут приведены конструкции для построения МП-автомата по заданной КС-грамматике, и наоборот. Также будут приведены теоремы об эквивалентности языков.

Построение МП-автомата по заданной КС-грамматике

Пусть [math] G=(V,T,Q,S) [/math] — КС-грамматика. Построим МП-автомат [math] P=(\{q\},T,V \cup T, \delta ,q,S) [/math], который допускает [math] L(G) [/math] по пустому магазину. Функция переходов [math] \delta [/math] будет определена по следующим правилам:

• 1. [math] \delta(q,\epsilon,A)=\{(q,\beta )| A \rightarrow \beta[/math] — продукция [math] G \} [/math] — для каждой переменной [math] A [/math].
• 2. [math] \delta(q,a,a)=\{(q,\epsilon)\} [/math] для каждого терминала [math] a [/math].

Пример

Преобразуем грамматику выражений в МП-автомат. Пусть дана грамматика:

• [math] I \rightarrow a|b|I1|I0|Ia|Ib [/math]
• [math] E \rightarrow I|E*E|E+E|(E) [/math]

Множеством входных символов является [math] \{a,b,1,0,(,),+,*\} [/math]. Эти символы, вместе с переменными [math] I,E [/math], образуют магазинный алфавит. Функция переходов определена следующим образом:

• a) [math] \delta(q,\epsilon,I)={(q,a), (q,b), (q,Ia), (q,Ib), (q,I0), (q,I1)};[/math]
• b) [math] \delta(q,\epsilon,E)={(q,I), (q,E+E), (q,E*E), (q,(E))};[/math]
• c) [math] \delta(q,a,a)=\{(q,\epsilon)\}[/math]; [math] \delta(q,b,b)=\{(q,\epsilon)\}[/math];...[math] \delta(q,*,*)=\{(q,\epsilon)\}[/math]; если входной символ совпадает с вершиной стека, то вершина удаляется.

Пункты a,b образованы по первому правилу построения функции переходов, пункт c по второму правилу.

Корректность построения

Пусть [math] w\in L(G)[/math], тогда [math] w [/math] имеет следующее левое порождение: [math] S = \gamma_1 \Rightarrow \gamma_2 \Rightarrow ... \Rightarrow \gamma_n=w[/math]. Покажем индукцией по [math] i [/math], что [math] (q,w,S)\vdash^*(q,y_i,\alpha_i)[/math]:

• База. Очевидно, что [math] (q,w,S)\vdash^*(q,w,S) [/math]
• Переход. Предположим, что [math] (q,w,S)\vdash^*(q,w_i,\alpha_i) [/math]. Заметим, что шаг порождения [math] y_i \Rightarrow y_{i+1}[/math] включает замену некоторой переменной [math] A [/math] ее продукцией [math] \beta [/math]. Правило 1 построения МП-автомата позволяет на заменить [math] A [/math] на вершине стека на цепочку [math] \beta [/math], а правило 2 позволяет затем сравнить любые терминалы на вершине со входными символами. В результате достигается МО [math] (q,y_{i+1},\alpha_{i+1}) [/math].
• Также заметим, что [math] \alpha_n = \epsilon[/math]. Таким образом [math] (q,w,S)\vdash^*(q,\epsilon,\epsilon) [/math], т.е допускает [math] P [/math] по пустому стеку.

Утверждение (1):

Если МП-автомат [math] P [/math] построен по грамматике [math] G [/math], с использованием указанной выше конструкции, то [math] N(P) \geq L(G) [/math]

[math]\triangleright[/math]

Очевидно из того, что мы доказали корректность построения.

[math]\triangleleft[/math]

Построение КС-грамматики по МП-автомату

Наша конструкция эквивалентной грамматики использует переменные вида: [math] [pXq][/math] — которая означает, что в процессе изменения состояния автомата от [math] p [/math] до [math] q [/math], [math] X [/math] удалилось из стека.
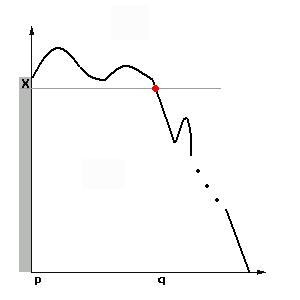Следует отметить, что удаление [math] X [/math] может являться результатом множества переходов.
Пусть [math] P=(Q,\Sigma,\Gamma,\delta,q_0,Z_0)[/math] — МП-автомат. Построим [math] G=(V,\Sigma,R,S)[/math], где [math] V [/math] состоит из:

• 1 Специальный стартовый символ [math] S [/math]
• 2 Все символы вида [math] [pXq][/math], где [math] p [/math] и [math] q [/math] — состояния из [math] Q [/math], а [math] X [/math] — магазинный символ из [math] \Gamma [/math].

Грамматика [math] G [/math] имеет следующие продукции:

• a) продукции [math] S \rightarrow [q_0,Z_0,p] [/math] для всех [math] p [/math], таким образом [math] (q,w,Z_0)\vdash^* (q,\epsilon,\epsilon)[/math]
• b) пусть [math] \delta(q,a,X) [/math] содержит [math] (r,Y_1,Y_2,...,Y_k)[/math]. Тогда для всех списков состояний [math] r_1,r_2,...,r_k[/math] в грамматике [math] G [/math] есть продукция [math] [qXr_k]\rightarrow a[r Y_1 r_1][r_1 Y_1 r_2]...[r_{k-1} Y_k r_k][/math].

Корректность построения

Докажем, что если [math] (q,w,X) \vdash^* (p,\epsilon,\epsilon)[/math], то [math] [q,X,p] \Rightarrow^* w [/math].