Переобучение — различия между версиями
Rugpanov (обсуждение | вклад) м |
Rugpanov (обсуждение | вклад) |
||
| Строка 31: | Строка 31: | ||
== High variance и high bias == | == High variance и high bias == | ||
| + | '''Bias''' - ошибка неверных предположений в алгоритме обучения. Высокий bias может привести к недообучению. | ||
| + | |||
| + | '''Variance''' - это ошибка, вызванная большой чувствительностью к небольшим отклонениям в тренировочном наборе. Высокая дисперсия может привести к переобучению. | ||
| + | The variance is an error from sensitivity to small fluctuations in the training set. High variance can cause an algorithm to model the random noise in the training data, rather than the intended outputs (overfitting). | ||
[[Файл:High_bias.jpg|border|500px|High variance и high bias]] | [[Файл:High_bias.jpg|border|500px|High variance и high bias]] | ||
Версия 00:17, 3 декабря 2018
Переобучение (англ. overfitting) — негативное явление, возникающее, когда алгоритм обучения вырабатывает предсказания, которые слишком близко или точно соответствуют конкретному набору данных, и поэтому не подходят для применения алгоритма к дополнительным данным или будущим наблюдениям.
Недообучение (англ. underfitting) — негативное явление, возникающее, когда выбранная статистическая модель не может адекватно описать базовую структуру данных.
Содержание
Примеры
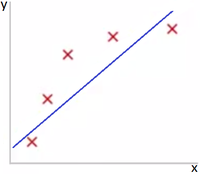
На примере линейной регрессии
Представьте задачу предсказания по . Рис 1 показывает результат использования модели для представленного датасета. Как видно из Рис 1 данные не поддаются линейной зависимости, и по этой причине модель не очень хороша.
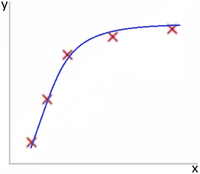
Если же добавить дополнительный параметр , и использовать модель , как представлено на Рис 2, то модель значительно лучше подходит для представленного датасета. Рис 3 показывает результат использования модели для представленного датасета. Как видно из Рис 3 данная модель слишком заточена для обучающего датасета и, веротяно, покажет плохой результат на тестовой.
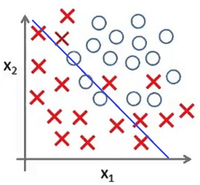
На примере логистической регрессии
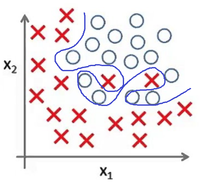
Представьте задачу классификации размеченых точек. Рис 4 показывает результат использования модели для представленного датасета. Как и в предыдущем примере, данные не поддаются классификации по линейной зависимости.
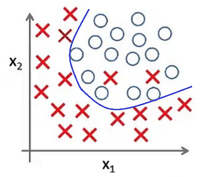
В случае же выбора модели , представленой на Рис 5, данные значительно лучше соответствуют модели. Рис 6 показывает результат использования модели для представленного датасета — это яркий пример явления переобучения.
Кривые обучения
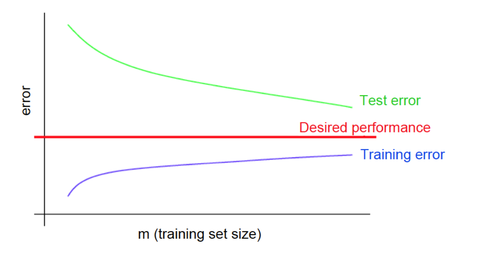
Кривые обучения при переобучении
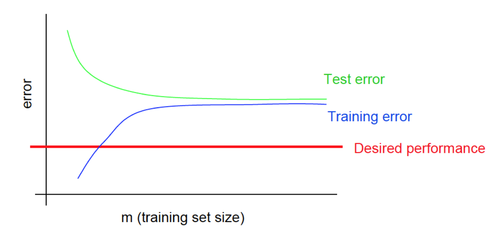
Кривые обучения при недообучении
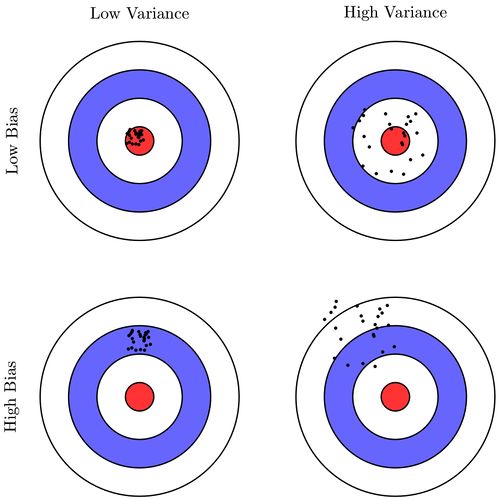
High variance и high bias
Bias - ошибка неверных предположений в алгоритме обучения. Высокий bias может привести к недообучению.
Variance - это ошибка, вызванная большой чувствительностью к небольшим отклонениям в тренировочном наборе. Высокая дисперсия может привести к переобучению.
The variance is an error from sensitivity to small fluctuations in the training set. High variance can cause an algorithm to model the random noise in the training data, rather than the intended outputs (overfitting).
Возможные решения
Возможные решения при переобучении
- Увеличение количества данных в наборе
- Уменьшение количества параметров модели
- Добавление регуляризации / увеличение коэффициента регуляризации
Возможные решения при недообучении
- Добавление новых параметров модели
- Использование для описания модели функций с более высокой степенью
- Уменьшение коэффициента регуляризации
См. также
- Модель алгоритма и ее выбор[на 01.12.18 не создан]
- Оценка качества в задачах классификации и регрессии [на 01.12.18 не создан]
- Оценка качества в задаче кластеризации [на 01.12.18 не создан]
Примечания
- Overfitting: when accuracy measure goes wrong
- The Problem of Overfitting Data
- Overfitting in Machine Learning
Источники информации
- Overfitting - статься на Википедии
- Переобучение - вводная статься на MachineLearning.ru
- The Problem of Overfitting - курс Andrew Ng
- Hastie, T., Tibshirani, R., Friedman, J. The Elements of Statistical Learning, 2nd edition. — Springer, 2009. — 533 p.
- Vapnik V.N. Statistical learning theory. — N.Y.: John Wiley & Sons, Inc., 1998.
- Воронцов, К. В. Комбинаторная теория надёжности обучения по прецедентам: Дис. док. физ.-мат. наук: 05-13-17. — Вычислительный центр РАН, 2010. — 271 с.