Материал из Викиконспекты
|
|
| Строка 5: |
Строка 5: |
| | Остовное дерево минимально тогда и только тогда, когда любое ребро не из дерева является максимальным на цмкле, который образуется при его добавлении в дерево | | Остовное дерево минимально тогда и только тогда, когда любое ребро не из дерева является максимальным на цмкле, который образуется при его добавлении в дерево |
| | |proof= | | |proof= |
| − | [[Файл:граф Gr.png]] | + | [[Файл:Gr.png]] |
| | Легко заметить, что остовное дерево, не удовлетворяющее условию, не минимально: | | Легко заметить, что остовное дерево, не удовлетворяющее условию, не минимально: |
| | | | |
Версия 19:53, 15 января 2011
| Теорема (критерий минимальности остовного дерева Тарьяна): |
Остовное дерево минимально тогда и только тогда, когда любое ребро не из дерева является максимальным на цмкле, который образуется при его добавлении в дерево |
| Доказательство: |
| [math]\triangleright[/math] |
|
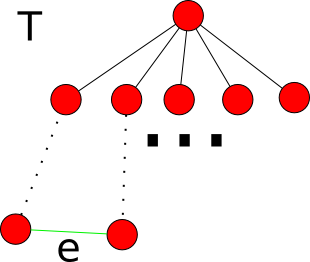 Легко заметить, что остовное дерево, не удовлетворяющее условию, не минимально:
Легко заметить, что остовное дерево, не удовлетворяющее условию, не минимально:
Если существует ребро, не максимальное на образовавшемся цикле мы можем уменьшить вес дерева, добавив это ребро и удалив максимальное.
Теперь докажем, что дерево, удовлетворяющее условию минимально:
Обозначим дерево [math]T[/math], покажем что его можно построить алгоритмом Крускала.
Индукция по количеству ребер в дереве:
База:
пустое дерево. Строим дерево [math]T'[/math] по лемме о безопасном ребре.
Переход:
Рассмотрим минимальное невзятое ребро [math]uv \in T[/math]
Рассмотрим разрез, окружающий одну из двух компонент
Пусть [math]uv[/math] не минимально в разрезе, тогда существует [math]ab \notin T[/math] такое, что [math]w(ab) \lt w(uv)[/math]. При добавлении [math]ab[/math] в дерево [math]T[/math] Некое ребро [math]xy[/math], такое что [math]w(xy) \ge w(uv) \lt w(ab)[/math] будет лежать на цикле. Противоречие условию теоремы.
Если [math]uv[/math] минимально - добавим его в [math]T'[/math].
По окончании (просмотрели все ребра [math]T[/math]) [math]T[/math] совпадет с [math]T'[/math] |
| [math]\triangleleft[/math] |
