Методы policy gradient и алгоритм асинхронного актора-критика — различия между версиями
(Новая страница: «== Policy gradient и алгоритм Actor-Critic == В алгоритме Q-learning агент обучает функцию полезности дейст…») |
|||
| Строка 1: | Строка 1: | ||
| − | |||
| − | |||
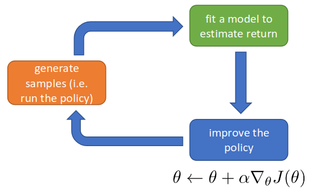
В алгоритме Q-learning агент обучает функцию полезности действия <tex>Q_{\theta}(s, a)</tex>. Стратегия агента <tex>\pi_{\theta}(a|s)</tex> определяется согласно текущим значениям <tex>Q(s, a)</tex>, с использованием жадного, <tex>\varepsilon</tex>-жадного или softmax подхода. Однако, существуют методы, которые позволяют оптимизировать стратегию <tex>\pi_{\theta}(s|a)</tex> напрямую. Такие алгоритмы относятся к классу алгоритмов ''policy gradient''. | В алгоритме Q-learning агент обучает функцию полезности действия <tex>Q_{\theta}(s, a)</tex>. Стратегия агента <tex>\pi_{\theta}(a|s)</tex> определяется согласно текущим значениям <tex>Q(s, a)</tex>, с использованием жадного, <tex>\varepsilon</tex>-жадного или softmax подхода. Однако, существуют методы, которые позволяют оптимизировать стратегию <tex>\pi_{\theta}(s|a)</tex> напрямую. Такие алгоритмы относятся к классу алгоритмов ''policy gradient''. | ||
| − | + | == Простой policy gradient алгоритм (REINFORCE) == | |
Рассмотрим МППР, имеющий терминальное состояние: задача - максимизировать сумму всех выигрышей <tex>R=r_0 + r_1+\cdots+r_T</tex>, где T - шаг, на котором произошел переход в терминальное состояние. | Рассмотрим МППР, имеющий терминальное состояние: задача - максимизировать сумму всех выигрышей <tex>R=r_0 + r_1+\cdots+r_T</tex>, где T - шаг, на котором произошел переход в терминальное состояние. | ||
| Строка 65: | Строка 63: | ||
Двигаясь вверх по этому градиенту, мы повышаем логарифм функции правдоподобия для сценариев, имеющих большой положительный <tex>R_{\tau}</tex>. | Двигаясь вверх по этому градиенту, мы повышаем логарифм функции правдоподобия для сценариев, имеющих большой положительный <tex>R_{\tau}</tex>. | ||
| − | + | == Преимущества и недостатки policy gradient по сравнению с Q-learning == | |
Преимущества: | Преимущества: | ||
| Строка 83: | Строка 81: | ||
Далее мы рассмотрим способы улучшения скорости работы алгоритма. | Далее мы рассмотрим способы улучшения скорости работы алгоритма. | ||
| − | + | == Усовершенствования алгоритма == | |
| − | + | === Опорные значения === | |
Заметим, что если <tex>b</tex> - константа относительно <tex>\tau</tex>, то | Заметим, что если <tex>b</tex> - константа относительно <tex>\tau</tex>, то | ||
| Строка 101: | Строка 99: | ||
, поэтому, регулируя <tex>b</tex>, можно достичь более низкой дисперсии, а значит, более быстрой сходимости Монте-Карло к истинному значению <tex>\nabla_{\theta} J(\theta)</tex>. Значение <tex>b</tex> называется ''опорным значением''. Способы определения опорных значений будут рассмотрены далее. | , поэтому, регулируя <tex>b</tex>, можно достичь более низкой дисперсии, а значит, более быстрой сходимости Монте-Карло к истинному значению <tex>\nabla_{\theta} J(\theta)</tex>. Значение <tex>b</tex> называется ''опорным значением''. Способы определения опорных значений будут рассмотрены далее. | ||
| − | + | === Использование будущего выигрыша вместо полного выигрыша === | |
Рассмотрим еще раз выражение для градиента полного выигрыша: | Рассмотрим еще раз выражение для градиента полного выигрыша: | ||
| Строка 113: | Строка 111: | ||
Величина <tex>Q_{\tau, t}</tex> -- ''будущий выигрыш'' (reward-to-go) на шаге <tex>t</tex> в сценарии <tex>\tau</tex> | Величина <tex>Q_{\tau, t}</tex> -- ''будущий выигрыш'' (reward-to-go) на шаге <tex>t</tex> в сценарии <tex>\tau</tex> | ||
| − | + | == Алгоритм Actor-Critic == | |
Из предыдущего абзаца: | Из предыдущего абзаца: | ||
Версия 20:53, 25 января 2019
В алгоритме Q-learning агент обучает функцию полезности действия . Стратегия агента определяется согласно текущим значениям , с использованием жадного, -жадного или softmax подхода. Однако, существуют методы, которые позволяют оптимизировать стратегию напрямую. Такие алгоритмы относятся к классу алгоритмов policy gradient.
Содержание
Простой policy gradient алгоритм (REINFORCE)
Рассмотрим МППР, имеющий терминальное состояние: задача - максимизировать сумму всех выигрышей , где T - шаг, на котором произошел переход в терминальное состояние.
Будем использовать букву для обозначения некоторого сценария - последовательности состояний и произведенных в них действий: . Будем обозначать сумму всех выигрышей, полученных в ходе сценария, как .
Не все сценарии равновероятны. Вероятность реализации сценария зависит от поведения среды, которое задается вероятностями перехода между состояниями и распределением начальных состояний , и поведения агента, которое определяется его стохастической стратегией . Вероятностное распределение над сценариями, таким образом, задается как
Будем максимизировать матожидание суммы полученных выигрышей:
Рассмотрим градиент оптимизируемой функции :
Считать градиент непосредственно сложно, потому что что - это большое произведение. Однако, так как
, мы можем заменить на :
Рассмотрим :
Тогда:
Подставляя в определение :
Как мы можем подсчитать это матожидание? С помощью семплирования (метод Монте-Карло). Если у нас есть N уже известных сценариев , то мы можем приблизить матожидание функции от сценария средним арифметическим этой функции по всему множеству сценариев:
Таким образом, оптимизировать можно с помощью следующего простого алгоритма (REINFORCE):
- Прогнать N сценариев со стратегией
- Посчитать среднее арифметическое
Интуитивное объяснение принципа работы
- это вероятность того, что будет реализован сценарий при условии параметров модели , т. е. функция правдоподобия. Нам хочется увеличить правдоподобие "хороших" сценариев (обладающих высоким ) и понизить правдоподобие "плохих" сценариев (с низким ).
Взглянем еще раз на полученное определение градиента функции полного выигрыша:
Двигаясь вверх по этому градиенту, мы повышаем логарифм функции правдоподобия для сценариев, имеющих большой положительный .
Преимущества и недостатки policy gradient по сравнению с Q-learning
Преимущества:
- Легко обобщается на задачи с большим множеством действий, в том числе на задачи с непрерывным множеством действий.
- По большей части избегает конфликта между exploitation и exploration, так как оптимизирует напрямую стохастическую стратегию .
- Имеет более сильные гарантии сходимости: если Q-learning гарантированно сходится только для МППР с конечными множествами действий и состояний, то policy gradient, при достаточно точных оценках (т. е. при достаточно больших выборках сценариев), сходится к локальному оптимуму всегда, в том числе в случае бесконечных множеств действий и состояний, и даже для частично наблюдаемых Марковских процессов принятия решений (POMDP).
Недостатки:
- Очень низкая скорость работы -- требуется большое количество вычислений для оценки по методу Монте-Карло, так как:
- для получения всего одного семпла требуется произвести взаимодействий со средой;
- случайная величина имеет большую дисперсию, так как для разных значения могут очень сильно различаться, поэтому для точной оценки требуется много семплов;
- cемплы, собранные для предыдущих значений , никак не переиспользуются на следующем шаге, семплирование нужно делать заново на каждом шаге градиентного спуска.
- В случае конечных МППР Q-learning сходится к глобальному оптимуму, тогда как policy gradient может застрять в локальном.
Далее мы рассмотрим способы улучшения скорости работы алгоритма.
Усовершенствования алгоритма
Опорные значения
Заметим, что если - константа относительно , то
, так как
Таким образом, изменение на константу не меняет оценку . Однако дисперсия зависит от :
, поэтому, регулируя , можно достичь более низкой дисперсии, а значит, более быстрой сходимости Монте-Карло к истинному значению . Значение называется опорным значением. Способы определения опорных значений будут рассмотрены далее.
Использование будущего выигрыша вместо полного выигрыша
Рассмотрим еще раз выражение для градиента полного выигрыша:
Так как в момент времени от действия зависят только для , это выражение можно переписать как
Величина -- будущий выигрыш (reward-to-go) на шаге в сценарии
Алгоритм Actor-Critic
Из предыдущего абзаца:
Здесь -- это оценка будущего выигрыша из состояния при условии действия , которая базируется только на одном сценарии . Это плохое приближение ожидаемого будущего выигрыша -- истинный ожидаемый будущий выигрыш выражается формулой
Также, в целях уменьшения дисперсии случайной величины, введем опорное значение для состояния , которое назовем ожидаемой ценностью (value) этого состояния. Ожидаемая ценность состояния -- это ожидаемый будущий выигрыш при совершении некоторого действия в этом состоянии согласно стратегии :
Таким образом, вместо ожидаемого будущего выигрыша при оценке будем использовать функцию преимущества (advantage):
Преимущество действия в состоянии -- это величина, характеризующая то, насколько выгоднее в состоянии выбрать именно действие .
Итого:
Как достаточно точно и быстро оценить ? Сведем задачу к оценке :
Теперь нам нужно уметь оценивать . Мы можем делать это, опять же, с помощью метода Монте-Карло -- так мы получим несмещенную оценку. Но это будет работать не существенно быстрее, чем обычный policy gradient. Вместо этого заметим, что при фиксированных и выполняется:
Таким образом, если мы имеем некоторую изначальную оценку для всех , то мы можем обновлять эту оценку путем, аналогичным алгоритму Q-learning:
Такой пересчет мы можем производить каждый раз, когда агент получает вознаграждение за действие.