Сегментация изображений

Сегментация изображения - это задача поиска групп пикселей, которые «идут вместе». В статистике эта проблема известна как кластерный анализ и является широко изученной областью с сотнями различных алгоритмов. В компьютерном зрении сегментация изображения является одной из старейших и широко изучаемых проблем.

В более ранних техниках используется расщепление и слияние регионов, что соответствует разделительным и агломерационным алгоритмам в литературе по кластеризации. Современные алгоритмы чаще оптимизируют некоторые глобальные критерии, такие как внутрирегиональная согласованность и межрегиональные длины границ.

Графо-ориентированная сегментация

Это алгоритм объединения, который использует относительные различия между регионами, чтобы определить, какие из них следует объединить. Кроме того, он доказуемо оптимизирует глобальную метрику группировки. Введем меру отличия одного пикселя от другого [math]w(e)[/math], которая будет показывать, например, разницу цветовой интенсивности между восьмью соседями.

Для любого региона R, его внутренняя разница определяется как наибольшая мера отличия в минимальном остовном дереве региона,

[math]Int(R) = \displaystyle\min_{e \in MST(R)} w(e).[/math]

Для любых двух соседних областей, по крайней мере, с одним смежным ребром, соединяющим их вершины, разность между этими регионами определяется как ребро минимального веса, соединяющее эти два региона,

[math]Dif(R_1, R_2) = \displaystyle\min_{e = (v_1, v_2) | v_1 \in R_1, v_2 \in R_2} w(e).[/math]

Алгоритм объединяет любые две соседние области, разница которых меньше минимальной внутренней разности этих двух областей,

[math]MInt(R_1, R_2) = \min(Int(R_1) + \tau(R_1), Int(R_2) +\tau(R_2)),[/math]

где [math]\tau(R)[/math] - это эвристический штраф по региону, который был установлен [math]k / |R|[/math], однако, он может быть установлен на любую специфическую для области применения меру.

Объединяя области в порядке убывания разделяющих их ребер (можно эффективно оценить с использованием алгоритма минимального остовного дерева Крускала), они доказуемо дают сегментацию. Причем такую, в которой присутствуют как области, которые могли бы быть объединены, так и те, которые могут быть разделены, но в небольших количествах. Для окрестностей пикселей фиксированного размера время работы этого алгоритма составляет [math]O (N \log N)[/math], где [math]N[/math] - количество пикселей изображения, что делает его одним из самых быстрых алгоритмов сегментации.

На рисунке слева - исходное изображение, справа - сегментированное после применения данного алгоритма.
Данный алгоритм был представлен в статье Felzenszwalb, P. F. and Huttenlocher, D. P. (2004b). Efficient graph-based image segmentation.[1]

Метод нормализованных срезов

Mетод нормализованных срезов, исследует сходство между соседними пикселями и пытается разделить их на группы, которые в свою очередь связаны слабо. Рассмотрим простой пример.
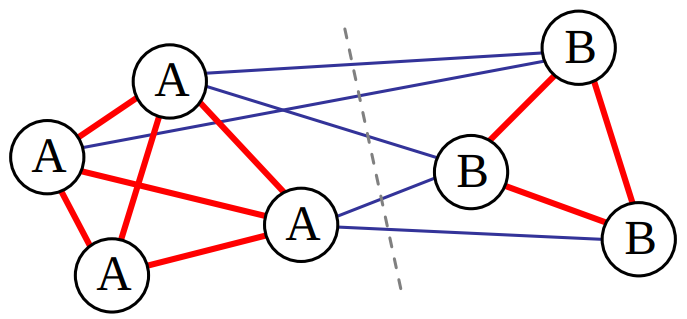
Все пиксели в группе A имеют высокое сходство, показаное в виде толстых красных линий, как и пиксели в группе B. Соединения между этими двумя группами, показанные в виде более тонких синих линий, намного слабее. Нормализованный разрез между двумя группами, показанный пунктирной линией, разделяет их на два кластера.

Разрез между двумя группами A и B определяется как сумма всех взвешенных весов,

[math]cut(A, B) = \displaystyle\sum_{i \in A, j \in B}w_{ij},[/math]

где веса между двумя пикселями [math]i[/math] и [math]j[/math] соответствуют их сходству. Однако использование минимального среза в качестве критерия сегментации не приводит к разумным кластерам, поскольку наименьшие срезы обычно предусматривают выделение одного пикселя.

Лучшей мерой сегментации является нормализованный срез, который определяется как

[math]Ncut(A,B)=\frac{cut(A,B)}{assoc(A, V)}+\frac{cut(A,B)}{assoc(B,V)},[/math]

где [math]assoc(A,A)=\sum_{i \in A, j \in A}w_{ij}[/math] это ассоциациея (сумма всех весов) в кластере и [math]assoc(A,V)=assoc(A,A)+cut(A,B)[/math]