Настройка глубокой сети — различия между версиями
Ventosa (обсуждение | вклад) (→Граф вычислений) |
Ventosa (обсуждение | вклад) |
||
| Строка 3: | Строка 3: | ||
== Инициализация сети == | == Инициализация сети == | ||
| − | Принцип выбора начальных значений весов для слоев, составляющих модель очень важен: установка всех весов в 0 будет серьезным препятствием для обучения, так как ни один из весов изначально не будет активен. Присваивать весам значения из интервала ±1 — тоже обычно не лучший вариант — на самом деле, иногда (в зависимости от задачи и сложности модели) от правильной инициализации модели может зависеть, достигнет она высочайшей производительности или вообще не будет сходиться. Даже если задача не предполагает такой крайности, удачно выбранный способ инициализации весов может значительно влиять на способность модели к обучению, так как он предустанавливает параметры модели с учетом функции потерь | + | Принцип выбора начальных значений весов для слоев, составляющих модель очень важен: установка всех весов в 0 будет серьезным препятствием для обучения, так как ни один из весов изначально не будет активен. Присваивать весам значения из интервала ±1 — тоже обычно не лучший вариант — на самом деле, иногда (в зависимости от задачи и сложности модели) от правильной инициализации модели может зависеть, достигнет она высочайшей производительности или вообще не будет сходиться. Даже если задача не предполагает такой крайности, удачно выбранный способ инициализации весов может значительно влиять на способность модели к обучению, так как он предустанавливает параметры модели с учетом функции потерь<ref>[https://habr.com/company/wunderfund/blog/315476/ Тонкая настройка нейронной сети, Habr]</ref>. |
Всегда можно выбрать случайно начальное приближение, но лучше выбирать определённым образом, ниже приведены самые распространённые из них. | Всегда можно выбрать случайно начальное приближение, но лучше выбирать определённым образом, ниже приведены самые распространённые из них. | ||
| − | Метод инициализации Завьера (Xavier) (иногда — метод Glorot’а)[http://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf]. Основная идея этого метода — упростить прохождение сигнала через слой во время как прямого, так и обратного распространения ошибки для линейной функции активации (этот метод также хорошо работает для сигмоидной функции, так как участок, где она ненасыщена, также имеет линейный характер). При вычислении весов этот метод опирается на вероятностное распределение (равномерное или нормальное) с дисперсией, равной <tex>\mathrm{Var}(W) = {2 \over{n_{in} + n_{out}}}</tex>, где <tex>n_{in}</tex> и <tex>n_{out}</tex> — количества нейронов в предыдущем и последующем слоях соответственно. | + | Метод инициализации Завьера (Xavier) (иногда — метод Glorot’а)<ref>[http://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf Understanding the difficulty of training deep feedforward neural networks]</ref>. Основная идея этого метода — упростить прохождение сигнала через слой во время как прямого, так и обратного распространения ошибки для линейной функции активации (этот метод также хорошо работает для сигмоидной функции, так как участок, где она ненасыщена, также имеет линейный характер). При вычислении весов этот метод опирается на вероятностное распределение (равномерное или нормальное) с дисперсией, равной <tex>\mathrm{Var}(W) = {2 \over{n_{in} + n_{out}}}</tex>, где <tex>n_{in}</tex> и <tex>n_{out}</tex> — количества нейронов в предыдущем и последующем слоях соответственно. |
| − | Метод инициализации Ге (He) — это вариация метода Завьера, больше подходящая функции активации ReLU, компенсирующая тот факт, что эта функция возвращает нуль для половины области определения. А именно, в этом случае <tex>\mathrm{Var}(W) = {2 \over{n_{in}}}</tex>[https://arxiv.org/pdf/1502.01852.pdf]. | + | Метод инициализации Ге (He) — это вариация метода Завьера, больше подходящая функции активации ReLU, компенсирующая тот факт, что эта функция возвращает нуль для половины области определения. А именно, в этом случае <tex>\mathrm{Var}(W) = {2 \over{n_{in}}}</tex><ref>[https://arxiv.org/pdf/1502.01852.pdf Delving Deep into Rectifiers]</ref>. |
== Граф вычислений == | == Граф вычислений == | ||
| Строка 18: | Строка 18: | ||
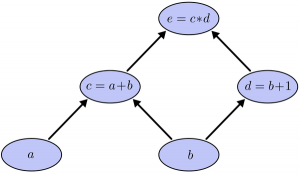
Значения, которые вводятся в узлы и выходят из узлов, называются тензорами (т.е. многомерными массивами). На рисунке 1 представлен граф вычислений для функции <tex>f(a,b)=(a+b)*(b+1)</tex>. В нейронах сетях функций имеют больше аргументов и сложнее, но смысл операций остаётся прежним. | Значения, которые вводятся в узлы и выходят из узлов, называются тензорами (т.е. многомерными массивами). На рисунке 1 представлен граф вычислений для функции <tex>f(a,b)=(a+b)*(b+1)</tex>. В нейронах сетях функций имеют больше аргументов и сложнее, но смысл операций остаётся прежним. | ||
| − | Процесс передачи значений от входных нейронов к выходным называется прямым распространеним (от англ. Forward pass). После чего мы вычисляем ошибку обработанных сетью данных на выходном нейроне и, основываясь на её значении, делаем обратную передачу (Back propagation)[https://en.wikipedia.org/wiki/Backpropagation]. Back propagation заключается в том, чтобы последовательно менять веса нейронной сети, начиная с весов выходного нейрона. Значения весов будут меняться в сторону уменьшения ошибки. | + | Процесс передачи значений от входных нейронов к выходным называется прямым распространеним (от англ. Forward pass). После чего мы вычисляем ошибку обработанных сетью данных на выходном нейроне и, основываясь на её значении, делаем обратную передачу (Back propagation)<ref>[https://en.wikipedia.org/wiki/Backpropagation Backpropagation, Wikipedia]</ref>. Back propagation заключается в том, чтобы последовательно менять веса нейронной сети, начиная с весов выходного нейрона. Значения весов будут меняться в сторону уменьшения ошибки. |
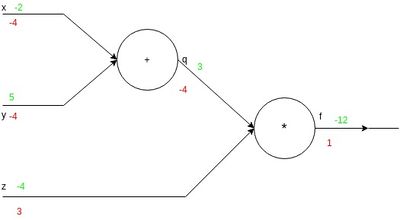
[[Файл: Graph_compilation.jpg|400px|thumb|Рис.2. Граф вычислений для функции <tex>f(x,y,z)=(x+y)*z</tex>. Зелёные цифры — значения вычислений по ходу выполнения операций графа, красные — значения производной выходной функции по текущей переменной в точке <tex>(x_0=-2, y_0=5, z_0=-4)</tex>]] | [[Файл: Graph_compilation.jpg|400px|thumb|Рис.2. Граф вычислений для функции <tex>f(x,y,z)=(x+y)*z</tex>. Зелёные цифры — значения вычислений по ходу выполнения операций графа, красные — значения производной выходной функции по текущей переменной в точке <tex>(x_0=-2, y_0=5, z_0=-4)</tex>]] | ||
| Строка 37: | Строка 37: | ||
Зная производные, можно искать матрицы весов <tex>w</tex> (числа, на которые умножаются входные для этого слоя значения) с помощью градиентного спуска сдвигаемся | Зная производные, можно искать матрицы весов <tex>w</tex> (числа, на которые умножаются входные для этого слоя значения) с помощью градиентного спуска сдвигаемся | ||
в сторону градиента (при максимизации) или обратную ему | в сторону градиента (при максимизации) или обратную ему | ||
| − | (при минимизации) <tex>w:=w-\eta\nabla_w f</tex>, или его модификаций [http://www.machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%B3%D1%80%D0%B0%D0%B4%D0%B8%D0%B5%D0%BD%D1%82%D0%BD%D0%BE%D0%B3%D0%BE_%D1%81%D0%BF%D1%83%D1%81%D0%BA%D0%B0]. | + | (при минимизации) <tex>w:=w-\eta\nabla_w f</tex>, или его модификаций<ref>[http://www.machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%B3%D1%80%D0%B0%D0%B4%D0%B8%D0%B5%D0%BD%D1%82%D0%BD%D0%BE%D0%B3%D0%BE_%D1%81%D0%BF%D1%83%D1%81%D0%BA%D0%B0 Метод градиентного спуска]</ref>. |
== Способы настройки параметров == | == Способы настройки параметров == | ||
| − | Ниже представлены различные вариации градиентного спуска (более подробное сравнение, применительно к данной задаче [https://habr.com/post/318970/]). | + | Ниже представлены различные вариации градиентного спуска (более подробное сравнение, применительно к данной задаче <ref>[https://habr.com/post/318970/ Методы оптимизации нейронных сетей, Habr]</ref>). |
| − | * Стохастический градиентный спуск [http://www.machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D1%81%D1%82%D0%BE%D1%85%D0%B0%D1%81%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B3%D0%BE_%D0%B3%D1%80%D0%B0%D0%B4%D0%B8%D0%B5%D0%BD%D1%82%D0%B0]: <tex>w^{(0)}</tex> — начальные весы сети, <tex>w^{(k+1)}=w^{(k)}-\mu\frac{\partial L(w^{(k)})}{\partial w}</tex>; | + | * Стохастический градиентный спуск<ref>[http://www.machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D1%81%D1%82%D0%BE%D1%85%D0%B0%D1%81%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B3%D0%BE_%D0%B3%D1%80%D0%B0%D0%B4%D0%B8%D0%B5%D0%BD%D1%82%D0%B0 Метод стохастического градиента]</ref>: <tex>w^{(0)}</tex> — начальные весы сети, <tex>w^{(k+1)}=w^{(k)}-\mu\frac{\partial L(w^{(k)})}{\partial w}</tex>; |
| − | * Momentum | + | * Momentum <ref>[https://en.wikipedia.org/wiki/Stochastic_gradient_descent#Momentum Momentum, Wikipedia]</ref>: <tex> \Delta w:=\alpha \Delta w-\eta \nabla Q_{i}(w)</tex>, <tex> w:=w+\Delta w</tex> или <tex> w:=w-\eta \nabla Q_{i}(w)+\alpha \Delta w</tex>; |
| − | * NAG (Nesterov accelerated gradient)[https://jlmelville.github.io/mize/nesterov.html#nag]: <tex> w^{(k+1)} = w^{(k)}-v^{(k)}; v^{(k+1)}=\gamma v^{(k)}+\mu\frac{\partial L(w^{(k)}-v^{(k)})}{\partial w}</tex> | + | * NAG (Nesterov accelerated gradient)<ref>[https://jlmelville.github.io/mize/nesterov.html#nag Nesterov accelerated gradient]</ref>: <tex> w^{(k+1)} = w^{(k)}-v^{(k)}; v^{(k+1)}=\gamma v^{(k)}+\mu\frac{\partial L(w^{(k)}-v^{(k)})}{\partial w}</tex> |
| − | *Adagrad [http://akyrillidis.github.io/notes/AdaGrad]: <tex>g_{i,(k)}=\frac{\partial L(w_i^{(k)})}{\partial w_i}, w_i^{(k+1)}=w_i^{(k)}-\frac{\mu}{\sqrt{G^{(k)}_i,i+\epsilon}}g_{i,(k)}</tex>, где G — диагональная матрица, элементы которой, суммы квадратов координат градиента к k-ой итерации алгоритма; | + | *Adagrad<ref>[http://akyrillidis.github.io/notes/AdaGrad AdaGrad]</ref>: <tex>g_{i,(k)}=\frac{\partial L(w_i^{(k)})}{\partial w_i}, w_i^{(k+1)}=w_i^{(k)}-\frac{\mu}{\sqrt{G^{(k)}_i,i+\epsilon}}g_{i,(k)}</tex>, где G — диагональная матрица, элементы которой, суммы квадратов координат градиента к k-ой итерации алгоритма; |
| − | *RMSProp[https://towardsdatascience.com/a-look-at-gradient-descent-and-rmsprop-optimizers-f77d483ef08b]: <tex>E^{(k)}[g_i^2] = \gamma E^{(k-1)}[g_i^2]+(1-\gamma)g^2_{i, (k)}, w^{(k+1)}_i = w_i^{(k)}-\frac{\mu}{\sqrt{E^{(k)}[g_i^2]+\epsilon}}g_{i, (k)}</tex>; | + | *RMSProp<ref>[https://towardsdatascience.com/a-look-at-gradient-descent-and-rmsprop-optimizers-f77d483ef08b RMSProp]</ref>: <tex>E^{(k)}[g_i^2] = \gamma E^{(k-1)}[g_i^2]+(1-\gamma)g^2_{i, (k)}, w^{(k+1)}_i = w_i^{(k)}-\frac{\mu}{\sqrt{E^{(k)}[g_i^2]+\epsilon}}g_{i, (k)}</tex>; |
| − | *Adadelta[https://arxiv.org/abs/1212.5701]:<tex>w^{(k+1)}=w^{(k)}-\mu(Q''(w^{(k)})^{-1}Q'(w^{(k)}</tex>, вычисление матрицы Q вторых производных довольно сложная задача, поэтому вместо неё можно брать приближение: <tex>w^{(k+1)}=w^{(k)}-\frac{RMS^{(k-1)}[\delta w_i}{RMS^{(k)}[g_i]}g_i^{(k)}</tex>, где <tex>RMS^{(k)}[x_i]=\sqrt{E^{(k)}[x^2_i]+\epsilon}</tex>; | + | *Adadelta<ref>[https://arxiv.org/abs/1212.5701 Adadelta]</ref>:<tex>w^{(k+1)}=w^{(k)}-\mu(Q''(w^{(k)})^{-1}Q'(w^{(k)}</tex>, вычисление матрицы Q вторых производных довольно сложная задача, поэтому вместо неё можно брать приближение: <tex>w^{(k+1)}=w^{(k)}-\frac{RMS^{(k-1)}[\delta w_i}{RMS^{(k)}[g_i]}g_i^{(k)}</tex>, где <tex>RMS^{(k)}[x_i]=\sqrt{E^{(k)}[x^2_i]+\epsilon}</tex>; |
| − | *Adam[https://arxiv.org/pdf/1412.6980.pdf]: <tex> w^{(k+1)}_i = w_i^{(k)}-\frac{\mu}{\sqrt{\hat{b}^2_{(k)}+\epsilon}}\hat{m}_{(k)}</tex>, где <tex>\hat{m}_{(k)}=\frac{\gamma_1 E^{(k-1)}[g_i]+(1-\gamma_1)g_{i,(k)}}{1-\gamma_1^k}</tex> и <tex>\hat{b}^2_{(k)}= \frac{\gamma_2 E^{(k-1)}[g^2_i]+(1-\gamma_2)g:2_{i,(k)}}{1-\gamma_2^k}</tex>. | + | *Adam<ref>[https://arxiv.org/pdf/1412.6980.pdf Adam]</ref>: <tex> w^{(k+1)}_i = w_i^{(k)}-\frac{\mu}{\sqrt{\hat{b}^2_{(k)}+\epsilon}}\hat{m}_{(k)}</tex>, где <tex>\hat{m}_{(k)}=\frac{\gamma_1 E^{(k-1)}[g_i]+(1-\gamma_1)g_{i,(k)}}{1-\gamma_1^k}</tex> и <tex>\hat{b}^2_{(k)}= \frac{\gamma_2 E^{(k-1)}[g^2_i]+(1-\gamma_2)g:2_{i,(k)}}{1-\gamma_2^k}</tex>. |
==См.также== | ==См.также== | ||
| Строка 64: | Строка 64: | ||
==Примечания== | ==Примечания== | ||
<references/> | <references/> | ||
| + | |||
==Источники информации== | ==Источники информации== | ||
| − | + | ||
| − | + | #[http://www.machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B0%D1%88%D0%B8%D0%BD%D0%BD%D0%BE%D0%B5_%D0%BE%D0%B1%D1%83%D1%87%D0%B5%D0%BD%D0%B8%D0%B5_%28%D0%BA%D1%83%D1%80%D1%81_%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D0%B9%2C_%D0%9A.%D0%92.%D0%92%D0%BE%D1%80%D0%BE%D0%BD%D1%86%D0%BE%D0%B2%29 Курс лекций по машинному обучению] {{---}} Воронцов К.В. | |
| − | + | # Riedmiller, M., & Braun, H. (1993). A direct adaptive method for faster backpropagation learning: The RPROP algorithm. In Neural Networks, 1993., IEEE International Conference on (pp. 586-591). IEEE. | |
| − | + | ||
| − | |||
| − | # http://www.machinelearning.ru/wiki/index.php?title=%D0%9C%D0% | ||
| − | |||
| − | # | ||
| − | |||
| − | |||
| − | |||
| − | |||
[[Категория: Машинное обучение]] | [[Категория: Машинное обучение]] | ||
[[Категория: Глубокое обучение]] | [[Категория: Глубокое обучение]] | ||
Версия 08:03, 27 января 2019
Глубокая сеть состоит из нескольких слоев, где каждый слой организован таким образом, что каждый нейрон в одном слое получает свою копию всех выходных данных предыдущего слоя. Эта модель идеально подходит для определенных типов задач, например, обучение на ограниченном количество более или менее неструктурированных параметров. Существует множество способов изменения параметров (весов) в такой модели, когда ей на вход поступают необработанные данные.
Содержание
Инициализация сети
Принцип выбора начальных значений весов для слоев, составляющих модель очень важен: установка всех весов в 0 будет серьезным препятствием для обучения, так как ни один из весов изначально не будет активен. Присваивать весам значения из интервала ±1 — тоже обычно не лучший вариант — на самом деле, иногда (в зависимости от задачи и сложности модели) от правильной инициализации модели может зависеть, достигнет она высочайшей производительности или вообще не будет сходиться. Даже если задача не предполагает такой крайности, удачно выбранный способ инициализации весов может значительно влиять на способность модели к обучению, так как он предустанавливает параметры модели с учетом функции потерь[1].
Всегда можно выбрать случайно начальное приближение, но лучше выбирать определённым образом, ниже приведены самые распространённые из них.
Метод инициализации Завьера (Xavier) (иногда — метод Glorot’а)[2]. Основная идея этого метода — упростить прохождение сигнала через слой во время как прямого, так и обратного распространения ошибки для линейной функции активации (этот метод также хорошо работает для сигмоидной функции, так как участок, где она ненасыщена, также имеет линейный характер). При вычислении весов этот метод опирается на вероятностное распределение (равномерное или нормальное) с дисперсией, равной , где и — количества нейронов в предыдущем и последующем слоях соответственно.
Метод инициализации Ге (He) — это вариация метода Завьера, больше подходящая функции активации ReLU, компенсирующая тот факт, что эта функция возвращает нуль для половины области определения. А именно, в этом случае [3].
Граф вычислений
Глубокие сети являются особенной формой графа вычиcлений.
Граф вычислений — это ориентированный граф, узлы которого соответствуют операциям или переменным. Переменные могут передавать свое значение в операции, а операции могут передавать свои результаты в другие операции. Таким образом, каждый узел в графе определяет функцию переменных.
Значения, которые вводятся в узлы и выходят из узлов, называются тензорами (т.е. многомерными массивами). На рисунке 1 представлен граф вычислений для функции . В нейронах сетях функций имеют больше аргументов и сложнее, но смысл операций остаётся прежним.
Процесс передачи значений от входных нейронов к выходным называется прямым распространеним (от англ. Forward pass). После чего мы вычисляем ошибку обработанных сетью данных на выходном нейроне и, основываясь на её значении, делаем обратную передачу (Back propagation)[4]. Back propagation заключается в том, чтобы последовательно менять веса нейронной сети, начиная с весов выходного нейрона. Значения весов будут меняться в сторону уменьшения ошибки.
Преимуществом такого представления функции является простота вычисления производных. Используя следующие правила вычисления частных производных:
.
Рассмотрим граф вычислений на рисунке 2 с поданными на вход значениями . Подсчёт производных по графу вычислений производим от значения функции к значениям независимых переменных-входов.
- ,
- ,
Зная производные, можно искать матрицы весов (числа, на которые умножаются входные для этого слоя значения) с помощью градиентного спуска сдвигаемся в сторону градиента (при максимизации) или обратную ему (при минимизации) , или его модификаций[5].
Способы настройки параметров
Ниже представлены различные вариации градиентного спуска (более подробное сравнение, применительно к данной задаче [6]).
- Стохастический градиентный спуск[7]: — начальные весы сети, ;
- Momentum [8]: , или ;
- NAG (Nesterov accelerated gradient)[9]:
- Adagrad[10]: , где G — диагональная матрица, элементы которой, суммы квадратов координат градиента к k-ой итерации алгоритма;
- RMSProp[11]: ;
- Adadelta[12]:, вычисление матрицы Q вторых производных довольно сложная задача, поэтому вместо неё можно брать приближение: , где ;
- Adam[13]: , где и .
См.также
- Глубокое обучение
- Стохастический градиентный спуск[на 21.01.19 не создан]
Примечания
- ↑ Тонкая настройка нейронной сети, Habr
- ↑ Understanding the difficulty of training deep feedforward neural networks
- ↑ Delving Deep into Rectifiers
- ↑ Backpropagation, Wikipedia
- ↑ Метод градиентного спуска
- ↑ Методы оптимизации нейронных сетей, Habr
- ↑ Метод стохастического градиента
- ↑ Momentum, Wikipedia
- ↑ Nesterov accelerated gradient
- ↑ AdaGrad
- ↑ RMSProp
- ↑ Adadelta
- ↑ Adam
Источники информации
- Курс лекций по машинному обучению — Воронцов К.В.
- Riedmiller, M., & Braun, H. (1993). A direct adaptive method for faster backpropagation learning: The RPROP algorithm. In Neural Networks, 1993., IEEE International Conference on (pp. 586-591). IEEE.