Методы policy gradient и алгоритм асинхронного актора-критика

В алгоритме Q-learning агент обучает функцию полезности действия [math]Q_{\theta}(s, a)[/math]. Стратегия агента [math]\pi_{\theta}(a|s)[/math] определяется согласно текущим значениям [math]Q(s, a)[/math], с использованием жадного, [math]\varepsilon[/math]-жадного или softmax подхода. Однако, существуют методы, которые позволяют оптимизировать стратегию [math]\pi_{\theta}(s|a)[/math] напрямую. Такие алгоритмы относятся к классу алгоритмов policy gradient.

Простой policy gradient алгоритм (REINFORCE)

Рассмотрим Марковский процесс принятия решений (МППР), имеющий терминальное состояние: задача — максимизировать сумму всех выигрышей [math]R=r_0 + r_1+\cdots+r_T[/math], где T — шаг, на котором произошел переход в терминальное состояние.

Будем использовать букву [math]\tau[/math] для обозначения некоторого сценария - последовательности состояний и произведенных в них действий: [math]\tau = (s_1, a_1, s_2, a_2, ... s_T, a_T)[/math]. Будем обозначать сумму всех выигрышей, полученных в ходе сценария, как [math]R_{\tau} = \sum_{\tau} {r(s_t, a_t)}[/math].

Не все сценарии равновероятны. Вероятность реализации сценария зависит от поведения среды, которое задается вероятностями перехода между состояниями [math]p(s_{t+1}|s_{t}, a_{t})[/math] и распределением начальных состояний [math]p(s_1)[/math], и поведения агента, которое определяется его стохастической стратегией [math]\pi_{\theta}(a_t|s_t)[/math]. Вероятностное распределение над сценариями, таким образом, задается как

[math]p_{\theta}(\tau) = p_{\theta}(s_1, a_1, ... s_T, a_T) = p(s_1) \prod_{t=1}^{T} {\pi_{\theta}(a_t|s_t) p(s_{t+1}|s_t, a_t)}[/math]

Мы предполагаем, что вероятности переходов между состояниями агенту неизвестны, то есть у агента нет модели поведения окружающей среды (model-free learning).

Нам нужно выбрать такой набор параметров агента [math]\theta[/math], задающий [math]\pi_{\theta}(a|s)[/math], чтобы максимизировать матожидание суммы полученных выигрышей:

[math]J(\theta) = E_{\tau \sim p_{\theta}(\tau)} \left[ R_{\tau} \right] = \int {p_{\theta}(\tau) R_{\tau} d\tau}[/math]

Пусть мы хотим максимизировать функцию [math]J(\theta)[/math] методом градиентного подъема. Для этого нам необходимо уметь рассчитывать ее градиент:

[math]\nabla_{\theta} J(\theta) = \int {\nabla_{\theta}p_{\theta}(\tau) R_{\tau} d\tau} [/math]

Мы не можем подсчитать [math]\nabla_{\theta}p_{\theta}(\tau)[/math] напрямую, потому что в выражение для [math]p_{\theta}(\tau)[/math] входят вероятности переходов между состояниями, которые агенту неизвестны. Однако, так как

[math]p_{\theta}(\tau) \nabla_{\theta} \log p_{\theta}(\tau) = p_{\theta}(\tau) \frac{\nabla_{\theta}p_{\theta}(\tau)}{p_{\theta}(\tau)} = \nabla_{\theta}p_{\theta}(\tau)[/math],

то мы можем заменить [math]\nabla_{\theta}p_{\theta}(\tau)[/math] на [math]p_{\theta}(\tau) \nabla_{\theta} \log p_{\theta}(\tau)[/math]:

[math]\nabla_{\theta} J(\theta) = \int {p_{\theta}(\tau) \nabla_{\theta} \log p_{\theta}(\tau) R_{\tau} d\tau} = E_{\tau \sim p_{\theta}(\tau)} \left[ \nabla_{\theta} \log p_{\theta}(\tau) R_{\tau} \right][/math]

Рассмотрим [math]\log p_{\theta}(\tau)[/math]:

[math] \log p_{\theta}(\tau) = \log \left( p(s_1) \prod_{t=1}^{T} {\pi_{\theta}(a_t|s_t) p(s_{t+1}|s_t, a_t)} \right) = \log p(s_1) + \sum_{t=1}^{T} {\left( \log \pi_{\theta}(a_t|s_t) + \log p(s_{t+1}|s_t, a_t) \right)} [/math]

Тогда:

[math] \nabla_{\theta} \log p_{\theta}(\tau) = \underbrace{\nabla_{\theta} \log p(s_1)}_{=0} + \sum_{t=1}^{T} {\left( \nabla_{\theta} \log \pi_{\theta}(a_t|s_t) + \underbrace{\nabla_{\theta} \log p(s_{t+1}|s_t, a_t)}_{=0} \right)} = \sum_{t=1}^{T} {\nabla_{\theta} \log \pi_{\theta}(a_t|s_t)} [/math]

Подставляя в определение [math]\nabla_{\theta} J(\theta)[/math]:

[math] \nabla_{\theta} J(\theta) = E_{\tau \sim p_{\theta}(\tau)} \left[ \left( \sum_{t=1}^{T} {\nabla_{\theta} \log \pi_{\theta}(a_t|s_t)} \right) R_{\tau} \right] [/math]

Схема алгоритма REINFORCE

Заметим, что в получившееся выражение для [math]\nabla_{\theta} J(\theta)[/math] уже не входят напрямую значения [math]p(s_{t+1}|s_{t}, a_{t})[/math] и [math]p(s_1)[/math], которые нам неизвестны. Таким образом, если у нас есть в наличии сценарий [math]\tau[/math] и соответствующее ему значение [math]R_\tau[/math], мы можем вычислить величину [math]\left( \sum_{t=1}^{T} {\nabla_{\theta} \log \pi_{\theta}(a_t|s_t)} \right) R_{\tau}[/math]. Значит, если у нас есть выборка из [math]N[/math] уже известных сценариев [math]\tau^i = (s_1^i, a_1^i, ... s_{T^i}^i, a_{T^i}^i)[/math], полученная из распределения [math]\tau \sim p_{\theta}(\tau)[/math],то мы можем приблизить посчитать приблизительное значение [math]\nabla_{\theta} J(\theta)[/math] по методу Монте-Карло — вычислив выборочное среднее случайной величины:

[math] \nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^N { \left( \sum_{t=1}^{T} {\nabla_{\theta} \log \pi_{\theta}(a_t^i|s_t^i)} \right) R_{\tau^i}} = \frac{1}{N} \sum_{i=1}^N { \left( \sum_{t=1}^{T^i} {\nabla_{\theta} \log \pi_{\theta}(a_t^i|s_t^i)} \right) \left( \sum_{t=1}^{T^i} { r(s_t^i, a_t^i) } \right)} [/math]

Осталось понять, как получить несмещенную выборку сценариев [math]\tau[/math] из вероятностного распределения [math]p_{\theta}(\tau)[/math]. Однако, это очень просто — нам всего лишь нужно зафиксировать параметр [math]\theta[/math] и провзаимодействовать со средой, так как распределение [math]p_{\theta}(\tau)[/math] задает именно вероятность реализации сценария [math]\tau[/math] при взаимодействии агента с фиксированной стратегией со средой.

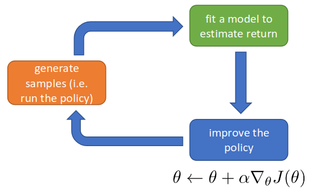
Таким образом, оптимизировать [math]J(\theta)[/math] можно с помощью следующего простого алгоритма (REINFORCE):

1. Прогнать [math]N[/math] сценариев [math]\tau_i[/math] со стратегией [math]\pi_{\theta}(a|s)[/math]
2. Посчитать среднее арифметическое [math]\nabla_{\theta} J(\theta) \leftarrow \frac{1}{N} \sum_{i=1}^N { \left( \sum_{t=1}^{T^i} {\nabla_{\theta} \log \pi_{\theta}(a_t^i|s_t^i)} \right) \left( \sum_{t=1}^{T^i} { r(s_t^i, a_t^i) } \right)}[/math]
3. [math] \theta \leftarrow \theta + \alpha \nabla_{\theta} J(\theta)[/math]
4. Если не сошлись к экстремуму, повторить с пункта 1.

Интуитивное объяснение принципа работы

Иллюстрация выбора наилучшего сценария

[math]p_{\theta}(\tau)[/math] - это вероятность того, что будет реализован сценарий [math]\tau[/math] при условии параметров модели [math]\theta[/math], т. е. функция правдоподобия. Нам хочется увеличить правдоподобие "хороших" сценариев (обладающих высоким [math]R_{\tau}[/math]) и понизить правдоподобие "плохих" сценариев (с низким [math]R_{\tau}[/math]).

Взглянем еще раз на полученное определение градиента функции полного выигрыша:

[math]\nabla_{\theta} J(\theta) = E_{\tau \sim p_{\theta}(\tau)} \left[ \nabla_{\theta} \log p_{\theta}(\tau) R_{\tau} \right][/math]

Двигаясь вверх по этому градиенту, мы повышаем логарифм функции правдоподобия для сценариев, имеющих большой положительный [math]R_{\tau}[/math].

Преимущества и недостатки policy gradient по сравнению с Q-learning

Преимущества:

• Легко обобщается на задачи с большим множеством действий, в том числе на задачи с непрерывным множеством действий.
• По большей части избегает конфликта между эксплуатацией (exploitation) и исследованием (exploration), так как оптимизирует напрямую стохастическую стратегию [math]\pi_{\theta}(a|s)[/math].
• Имеет более сильные гарантии сходимости: если Q-learning гарантированно сходится только для МППР с конечными множествами действий и состояний, то policy gradient, при достаточно точных оценках [math]\nabla_{\theta} J(\theta)[/math] (т. е. при достаточно больших выборках сценариев), сходится к локальному оптимуму всегда, в том числе в случае бесконечных множеств действий и состояний, и даже для частично наблюдаемых Марковских процессов принятия решений (ЧНМППР, англ. partially observed Markov decision process, POMDP).

Недостатки:

• Очень низкая скорость работы — требуется большое количество вычислений для оценки [math]\nabla_{\theta} J(\theta)[/math] по методу Монте-Карло, так как:
  • для получения всего одного семпла требуется произвести [math]T[/math] взаимодействий со средой;
  • случайная величина [math]\nabla_{\theta} \log p_{\theta}(\tau) R_{\tau}[/math] имеет большую дисперсию, так как для разных [math]\tau[/math] значения [math]R_{\tau}[/math] могут очень сильно различаться, поэтому для точной оценки [math]\nabla_{\theta} J(\theta) = E_{\tau \sim p_{\theta}(\tau)} \left[ \nabla_{\theta} \log p_{\theta}(\tau) R_{\tau} \right][/math] требуется много семплов;
  • cемплы, собранные для предыдущих значений [math]\theta[/math], никак не переиспользуются на следующем шаге, семплирование нужно делать заново на каждом шаге градиентного спуска.
• В случае конечных МППР Q-learning сходится к глобальному оптимуму, тогда как policy gradient может застрять в локальном.

Далее мы рассмотрим способы ускорения работы алгоритма.

Усовершенствования алгоритма

Опорные значения

Заметим, что если [math]b[/math] - константа относительно [math]\tau[/math], то

[math]E_{\tau \sim p_{\theta}(\tau)} \left[ \nabla_{\theta} \log p_{\theta}(\tau) (R_{\tau} - b) \right] = E_{\tau \sim p_{\theta}(\tau)} \left[ \nabla_{\theta} \log p_{\theta}(\tau) R_{\tau} \right] [/math],

так как

[math]E_{\tau \sim p_{\theta}(\tau)} \left[ \nabla_{\theta} \log p_{\theta}(\tau) b \right] = \int {p_{\theta}(\tau) \nabla_{\theta} \log p_{\theta}(\tau) b d\tau} = \int {\nabla_{\theta} p_{\theta}(\tau) b d\tau} = b \nabla_{\theta} \int {p_{\theta}(\tau) d\tau} = b \nabla_{\theta} 1 = 0[/math]

Таким образом, изменение [math]R_{\tau}[/math] на константу не меняет оценку [math]\nabla_{\theta} J(\theta)[/math]. Однако дисперсия [math] Var_{\tau \sim p_{\theta}(\tau)} \left[ \nabla_{\theta} \log p_{\theta}(\tau) (R_{\tau} - b) \right][/math] зависит от [math]b[/math]:

[math] Var_{\tau \sim p_{\theta}(\tau)} \left[ \nabla_{\theta} \log p_{\theta}(\tau) (R_{\tau} - b) \right] = \underbrace{E_{\tau \sim p_{\theta}(\tau)} \left[ \left( \nabla_{\theta} \log p_{\theta}(\tau) (R_{\tau} - b) \right)^2 \right]}_{\text{depends on } b} - \underbrace{E_{\tau \sim p_{\theta}(\tau)} \left[ \nabla_{\theta} \log p_{\theta}(\tau) (R_{\tau} - b) \right]^2}_{= E \left[ \nabla_{\theta} \log p_{\theta}(\tau) R_{\tau} \right]^2} [/math],

поэтому, регулируя [math]b[/math], можно достичь более низкой дисперсии, а значит, более быстрой сходимости метода Монте-Карло к истинному значению [math]\nabla_{\theta} J(\theta)[/math]. Значение [math]b[/math] называется опорным значением. Способы определения опорных значений будут рассмотрены далее, в рамках рассмотрения алгоритма актора-критика (Actor-Critic).

Использование будущего выигрыша вместо полного выигрыша

Рассмотрим еще раз выражение для градиента полного выигрыша:

[math] \nabla_{\theta} J(\theta) = E_{\tau \sim p_{\theta}(\tau)} \left[ \left( \sum_{t=1}^{T} {\nabla_{\theta} \log \pi_{\theta}(a_t|s_t)} \right) R_{\tau} \right] = E_{\tau \sim p_{\theta}(\tau)} \left[ \sum_{t=1}^{T} {\nabla_{\theta} \log \pi_{\theta}(a_t|s_t)} \left( \sum_{t=1}^{T} {r(s_t, a_t)} \right) \right][/math]

Так как в момент времени [math]t[/math] от действия [math]a_t[/math] зависят только [math]r(s_{t'}, a_{t'})[/math] для [math] t' \leq t[/math], это выражение можно переписать как

[math] \nabla_{\theta} J(\theta) \approx E_{\tau \sim p_{\theta}(\tau)} \left[ \sum_{t=1}^{T} {\nabla_{\theta} \log \pi_{\theta}(a_t|s_t)} \underbrace{\left( \sum_{t'=t}^{T} {r(s_{t'}, a_{t'})} \right)}_{= Q_{\tau, t}} \right][/math]

Величина [math]Q_{\tau, t}[/math] -- будущий выигрыш (reward-to-go) на шаге [math]t[/math] в сценарии [math]\tau[/math]

Алгоритм Actor-Critic

Из предыдущего абзаца:

[math]\nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N} \sum_{t=1}^{T} {\nabla_{\theta} \log \pi_{\theta}(a_t^i|s_t^i) Q_{\tau_i, t} } [/math]

Здесь [math]Q_{\tau_i, t}[/math] — это оценка будущего выигрыша из состояния [math]s_t^i[/math] при условии действия [math]a_t^i[/math], которая базируется только на одном сценарии [math]\tau_i[/math]. Это плохое приближение ожидаемого будущего выигрыша — истинный ожидаемый будущий выигрыш выражается формулой

[math] Q^{\pi}(s_t, a_t) = \sum_{t'=t}^{T} {E_{\pi_{\theta}} [r(s_{t'}, a_{t'}) | s_t, a_t] } [/math]

Также, в целях уменьшения дисперсии случайной величины, введем опорное значение для состояния [math]s_t[/math], которое назовем ожидаемой ценностью (value) этого состояния. Ожидаемая ценность состояния [math]s_t[/math] -- это ожидаемый будущий выигрыш при совершении некоторого действия в этом состоянии согласно стратегии [math]\pi_{\theta}(a|s)[/math]:

[math] V^{\pi}(s_t) = E_{a_t \sim \pi_{\theta}(a_t | s_t)} [Q^{\pi}(s_t, a_t)] = \sum_{t'=t}^{T} {E_{\pi_{\theta}} [r(s_{t'}, a_{t'}) | s_t]}[/math]

Таким образом, вместо ожидаемого будущего выигрыша при оценке [math]\nabla_{\theta} J(\theta)[/math] будем использовать функцию преимущества (advantage):

[math] A^{\pi}(s_t, a_t) = Q^{\pi}(s_t, a_t) - V^{\pi}(s_t) [/math]

Преимущество действия [math]a_t[/math] в состоянии [math]s_t[/math] — это величина, характеризующая то, насколько выгоднее в состоянии [math]s_t[/math] выбрать именно действие [math]a_t[/math].

Итого:

[math] \nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N} \sum_{t=1}^{T} {\nabla_{\theta} \log \pi_{\theta}(a_t^i|s_t^i) A^{\pi}(s_t^i, a_t^i) } [/math]

Как достаточно точно и быстро оценить [math]A^{\pi}(s_t^i, a_t^i)[/math]? Сведем задачу к оценке [math]V^{\pi}(s_t)[/math]:

[math] Q^{\pi}(s_t, a_t) = r(s_t, a_t) + E_{s_{t+1} \sim p(s_{t+1} | s_t, a_t)} [V^{\pi}(s_{t+1})] \approx r(s_t, a_t) + V^{\pi}(s_{t+1}) [/math]

[math] A^{\pi}(s_t^i, a_t^i) = Q^{\pi}(s_t, a_t) - V^{\pi}(s_t) \approx r(s_t, a_t) + V^{\pi}(s_{t+1}) - V^{\pi}(s_t) [/math]

Теперь нам нужно уметь оценивать [math]V^{\pi}(s_t) = \sum_{t'=t}^{T} {E_{\pi_{\theta}} [r(s_{t'}, a_{t'}) | s_t] }[/math]. Мы можем делать это, опять же, с помощью метода Монте-Карло — так мы получим несмещенную оценку. Но это будет работать не существенно быстрее, чем обычный policy gradient. Вместо этого заметим, что при фиксированных [math]s_t[/math] и [math]a_t[/math] выполняется:

[math] V^{\pi}(s_t) = r(s_t, a_t) + V^{\pi}(s_{t+1})[/math]

Таким образом, если мы имеем некоторую изначальную оценку [math]V^{\pi}(s)[/math] для всех [math]s[/math], то мы можем обновлять эту оценку путем, аналогичным алгоритму Q-learning:

[math] V^{\pi}(s_t) \leftarrow (1 - \beta) V^{\pi}(s_t) + \beta (r(s_t, a_t) + V^{\pi}(s_{t+1})) [/math]

Здесь [math]\beta[/math] -- это коэффициент обучения (learning rate) для функции ценности. Такой пересчет мы можем производить каждый раз, когда агент получает вознаграждение за действие. Так мы получим оценку ценности текущего состояния, не зависящую от выбранного сценария развития событий [math]\tau[/math], а значит, и оценка функции преимущества не будет зависеть от выбора конкретного сценария. Это сильно снижает дисперсию случайной величины [math]\nabla_{\theta} \log \pi_{\theta}(a_t^i|s_t^i) A^{\pi}(s_t^i, a_t^i)[/math], что делает оценку [math]\nabla_{\theta} J(\theta)[/math] достаточно точной даже в том случае, когда мы используем всего один сценарий для ее подсчета:

[math]\nabla_{\theta} J(\theta) \approx \sum_{t=1}^{T} {\nabla_{\theta} \log \pi_{\theta}(a_t|s_t) A^{\pi}(s_t, a_t) }[/math]

На практике же мы можем аппроксимировать [math]\nabla_{\theta} J(\theta)[/math] на каждом шаге (в онлайне), основываясь на всего одном действии каждый раз. Алгоритм, в итоге, будет следующим:

1. производим действие [math]a \sim \pi_{\theta}(a|s)[/math], переходим в состояние [math]s'[/math] и получаем вознаграждение [math]r[/math]
2. [math]V^{\pi}(s) \leftarrow (1 - \beta) V^{\pi}(s) + \beta (r + V^{\pi}(s'))[/math]
3. [math]A_{\pi}(s, a) \leftarrow r + V^{\pi}(s') - V^{\pi}(s) [/math]
4. [math]\nabla_{\theta} J(\theta) \leftarrow \nabla_{\theta} \log \pi_{\theta}(a|s) A^{\pi}(s, a)[/math]
5. [math]\theta \leftarrow \theta + \alpha \nabla_{\theta} J(\theta)[/math]
6. Если не сошлись к экстремуму, повторить с пункта 1.

Такой алгоритм называется алгоритмом актора-критика с преимуществом (Advantage Actor-Critic). Актором здесь называется компонента, которая оптимизирует стратегию [math]\pi_{\theta}(a|s)[/math], а критиком — компонента, которая подсчитывает ценности состояний [math]V^{\pi}(s)[/math]. Актор определяет дальнейшее действие, а критик оценивает, насколько то или иное действие выгодно, основываясь на функции преимущества (advantage).

Алгоритм актора-критика считается гибридным, так как актор работает в соответствии с принципом policy gradient, а критик работает аналогично алгоритму Q-routing.

Асинхронный актор-критик

Иллюстрация работы алгоритма асинхронного актора-критика

Проблема с обучением с подкреплением в онлайне заключается в том, что данные, поступающие на вход алгоритму обучения, сильно скоррелированы: каждое следующее состояние непосредственно зависит от предпринятых агентом действий. Обучение на сильно скоррелированных данных приводит к переобучению. Таким образом, для того, чтобы успешно обучить стратегию, обобщаемую на большое количество состояний среды, нам все еще необходимо обучаться на эпизодах из различных сценариев.

Одним из способов достичь этого является запуск множества агентов параллельно. Все агенты находятся в разных состояниях и выбирают различные конкретные действия согласно стохастической стратегии [math]\pi_{\theta}(a|s)[/math], тем самым достигается устранение корреляции между наблюдаемыми данными. Однако, все агенты используют и оптимизируют один и тот же набор параметров [math]\theta[/math].

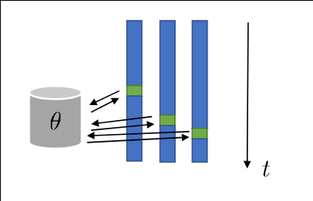
Идея алгоритма асинхронного актора-критика заключается в том, чтобы запустить [math]N[/math] агентов параллельно, при этом на каждом шаге каждый из агентов рассчитывает обновления для значений [math]V^{\pi}(s)[/math] и [math]\theta[/math]. Однако, вместо того, чтобы просто продолжить работу, каждый агент обновляет [math]V^{\pi}(s)[/math] и [math]\theta[/math], общие для всех агентов. Перед обработкой каждого нового эпизода агент копирует текущие глобальные значения параметра [math]\theta[/math] и использует его, чтобы определить собственную стратегию на этот эпизод. Агенты не ждут, пока остальные агенты завершат обработку своих эпизодов, чтобы обновить глобальные параметры (отсюда асинхронный). Поэтому, пока один из агентов обрабатывает один эпизод, глобальное значение [math]\theta[/math] может изменяться вследствие действий других агентов.

Реализация асинхронного актора-критика на основе нейронных сетей

Совместная архитектура нейросети для алгоритма актора-критика

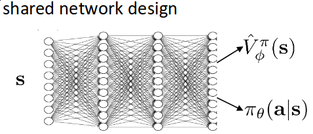
В большинстве современных исследований стратегия [math]\pi_{\theta}(a|s)[/math] и функция ценности [math]V^{\pi}(s)[/math] задаются с помощью нейросетей. Каждая из функций может в принципе использовать отдельную нейросеть, но на практике чаще всего применяется совмещенная нейросеть с двумя выходными слоями — для стратегии и для функции ценности. Такой подход, как правило, приводит к лучшим результатам, так как функция ценности, вообще говоря, зависит от текущей стратегии.

Реализация алгоритма асинхронного актора-критика инициализирует глобальную нейросеть (master network) и запускает N дочерних процессов (workers), в каждом из которых агент взаимодействует со средой. Нейросеть каждого агента является копией материнской нейросети. Перед началом каждого эпизода веса из материнской нейросети заново копируются в нейросеть агента. Градиенты, посчитанные по агентской нейросети, применяются в итоге к материнской.

См. также

• Обучение с подкреплением

Ссылки

• Williams, Ronald J. "Simple statistical gradient-following algorithms for connectionist reinforcement learning." Machine learning 8.3-4 (1992): 229-256.
• Sutton, Richard S., et al. "Policy gradient methods for reinforcement learning with function approximation." Advances in neural information processing systems. 2000.
• Policy Gradients. CS 294-112: Deep Reinforcement Learning, Sergey Levine.
• Actor-Critic Algorithms. CS 294-112: Deep Reinforcement Learning, Sergey Levine.
• Simple Reinforcement Learning with Tensorflow Part 8: Asynchronous Actor-Critic Agents (A3C)