Виды ансамблей

Ансамбль

Рассмотрим задачу классификации на K классов: [math]Y = \{1, 2, ..., K\}[/math]
Пусть имеется M классификатор ("экспертов"): [math] f_1, f_2, ..., f_M [/math]
[math] f_m : X \leftarrow Y, f_m \in F, m = (1 ... M) [/math]

Тогда давайте посмотрим новый классификатор на основе данных:

Простое голосование: [math] f(x) = \max \limits_{k = 1 .. K} \sum \limits_{i = 1}^M I(f_i(x) = k) [/math]
Взвешенное голосование: [math] f(x) = \max \limits_{k = 1 .. K} \sum \limits_{i = 1}^M \alpha_i I(f_i(x) = k), \sum \limits_i \alpha_i = 1, \alpha_i \gt 0[/math]

Вероятность ошибки

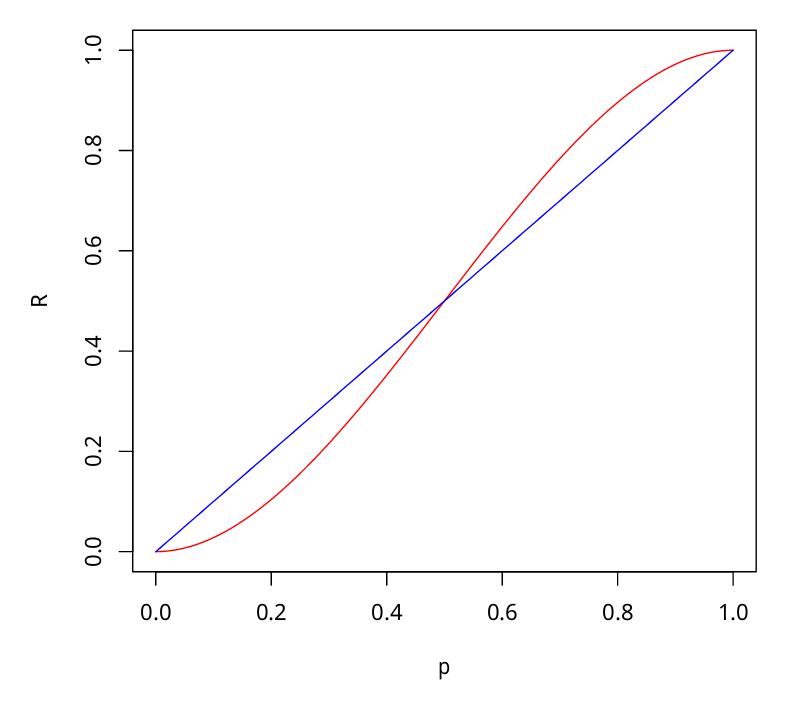
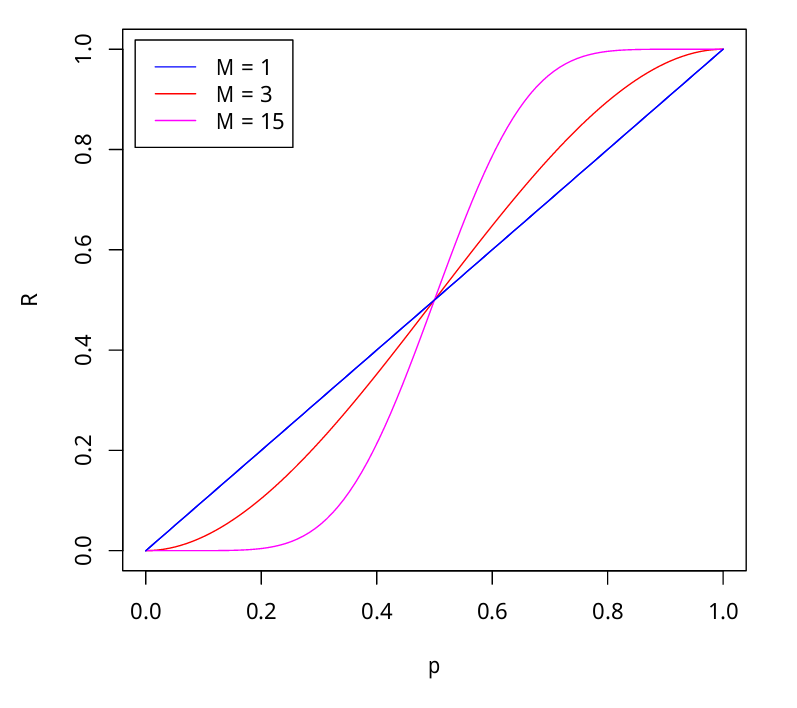
Пусть [math]M[/math] - количество присяжный, [math]p[/math] - вероятность правильного решения одного эксперта, [math]R[/math] - вероятность правильного решения всего жюри, [math]m[/math] - минимальное большинство членов жюри [math] = floor(N / 2) + 1 [/math]

Тогда [math] R = \sum \limits_{i = m}^M C_M^i p ^ i (1 - p) ^ {M - i} [/math]

Бутстрэп

Метод бутстрэпа (англ. bootstrap) — один из первых и самых простых видов ансамблей, который позволяет оценивать многие статистики сложных распределений и заключается в следующем. Пусть имеется выборка [math]X[/math] размера [math]N[/math]. Равномерно возьмем из выборки [math]N[/math] объектов с возвращением. Это означает, что мы будем [math]N[/math] раз равновероятно выбирать произвольный объект выборки, причем каждый раз мы выбираем из всех исходных [math]N[/math] объектов. Отметим, что из-за возвращения среди них окажутся повторы.
Обозначим новую выборку через [math]X_1[/math]. Повторяя процедуру [math]M[/math] раз, сгенерируем [math]M[/math] подвыборок [math]X_1 ... X_M[/math]. Теперь мы имеем достаточно большое число выборок и можем оценивать различные статистики исходного распределения.

Бутсреп используется в статистике, в том числе для:

• Аппроксимация стандартной ошибки выборочной оценки
• Байесовская коррекция с помощью бутстреп метода
• Доверительные интервалы
• Метод процентилей

Бэггинг

Пусть имеется выборка [math]X[/math] размера [math]N[/math]. Количество классификаторов [math]M[/math]

Алгоритм классификации в технологии бэггинг на подпространствах:

• Генерируется с помощью бутстрэпа M выборок размера N для каждого классификатора
• Производится независимое обучения каждого элементарного классификатора (каждого алгоритма, определенного на своем подпространстве).
• Производится классификация основной выборки на каждом из подпространств (также независимо).
• Принимается окончательное решение о принадлежности объекта одному из классов. Это можно сделать несколькими разными способами, подробнее описано ниже.

Окончательное решение о принадлежности объекта классу может приниматься, например, одним из следующих методов:

• Консенсус: если все элементарные классификаторы присвоили объекту одну и ту же метку, то относим объект к выбранному классу.
• Простое большинство: консенсус достижим очень редко, поэтому чаще всего используют метод простого большинства. Здесь объекту присваивается метка того класса, который определило для него большинство элементарных классификаторов.
• Взвешивание классификаторов: если классификаторов четное количество, то голосов может получиться поровну, еще возможно, что для эксперты одна из групп параметров важна в большей степени, тогда прибегают к взвешиванию классификаторов. То есть при голосовании голос классификатора умножается на его вес.

Эффективность

Рассмотрим задачу регрессии с базовыми алгоритмами [math]b_1, b_2, ..., b_m[/math]. Предположим, что существует истинная функция ответа для всех объектов y(x), а также задано распределение p(x) на объектах. В этом случае мы можем записать ошибку каждой функции регрессии:

[math] \epsilon_i(x) = b_i(x) - y(x), y = 1, ..., n [/math]

и записать матожидание среднеквадратичной ошибки:

[math]E_x(b_i(x) - y(x))^2 = E_x \epsilon_i^2(x) [/math]

Средняя ошибка построенных функций регрессии имеет вид:

[math]E_1 = \frac 1 n E_x \sum \limits_{i = 1}^n \epsilon_i^2(x) [/math]

Предположим, что ошибки несмещены и некоррелированы:

[math] E_x\epsilon_i(x) = 0, E_x\epsilon_i(x)\epsilon_j(x) = 0, i ≠ j [/math]

Построим теперь новую функцию регрессии, которая будет усреднять ответы построенных нами функций:

[math] a(x) = \frac 1 n \sum \limits_{i = 1}^n b_i(x) [/math]

Найдем ее среднеквадратичную ошибку:

[math] E_n = E_x(\frac 1 n \sum \limits_{i = 1}^n (b_i(x) - y(x))^2 = E_x(\frac 1 n \sum \limits_{i = 1}^n \epsilon_i)^2 = \frac 1 {n^2} E_x(\sum \limits_{i = 1}^n \epsilon_i^2(x) + \sum \limits_{i ≠ j} \epsilon_i(x)\epsilon_j(x)) = \frac 1 n E_1 [/math]

Таким образом, усреднение ответов позволило уменьшить средний квадрат ошибки в [math]n[/math] раз