Поиск ближайших соседей с помощью иерархического маленького мира — различия между версиями
(→Маленький мир) |
Marsermd (обсуждение | вклад) (→Маленький мир) |
||
| Строка 2: | Строка 2: | ||
==Маленький мир== | ==Маленький мир== | ||
| + | [[Файл:SmallWorld_Greedy.png|мини|500px|Жадный поиск ближайшего соседа. | ||
| + | Чёрные ребра {{---}} короткие связи с ближайшими соседями, красные рёбра {{---}} длинные связи, обеспечивающие малое мат. ожидание длины пути. | ||
| + | [https://www.hse.ru/mirror/pubs/lib/data/access/ram/ticket/30/1551306415713d428dca7fd05f3d108fe8e66042c4/Approximate%20nearest%20neighbor%20algorithm%20based%20on%20navigable%20(Information%20Systems).pdf Оригинал]]] | ||
'''Маленький мир''' (англ. ''Small World'') {{---}} граф, в котором мат. ожидание кратчайшего пути между двумя случайно выбранными вершинами растёт пропорционально <tex>\log{N}</tex>. Но при этом средняя степень вершины мала. | '''Маленький мир''' (англ. ''Small World'') {{---}} граф, в котором мат. ожидание кратчайшего пути между двумя случайно выбранными вершинами растёт пропорционально <tex>\log{N}</tex>. Но при этом средняя степень вершины мала. | ||
| Строка 23: | Строка 26: | ||
result.addAll(tempNearest) | result.addAll(tempNearest) | ||
'''return''' k первых вершин из nearest | '''return''' k первых вершин из nearest | ||
| + | |||
| + | Очевидный недостаток этого алгоритма {{---}} опасность свалиться в локальный минимум. | ||
==Описание структуры== | ==Описание структуры== | ||
Версия 00:09, 1 марта 2019
Иерархия навигируемых малых миров (англ. Hierarchical Navigable Small World) — структура данных, позволяющая эффективно находить K почти что ближайших соседей. По своей концепции напоминает список с пропусками.
Содержание
Маленький мир
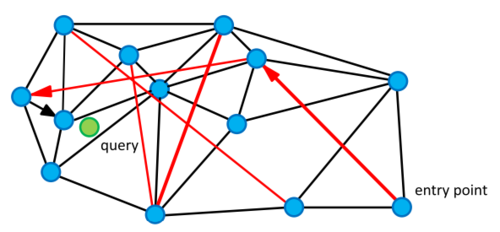
Жадный поиск ближайшего соседа. Чёрные ребра — короткие связи с ближайшими соседями, красные рёбра — длинные связи, обеспечивающие малое мат. ожидание длины пути. Оригинал
Маленький мир (англ. Small World) — граф, в котором мат. ожидание кратчайшего пути между двумя случайно выбранными вершинами растёт пропорционально . Но при этом средняя степень вершины мала.
Для маленького мира на точках в Евклидовом пространстве, приближенный поиск K ближайших соседей будет выглядеть так:
KNN(request, m, k):
nearest = new TreeSet() // вершины упорядочены по возрастанию расстояния до request
candidates = new TreeSet()
visited = new HashSet()
for i = 1 to m
candidates.add(случайная вершина графа)
tempNearest = new TreeMap()
while true
current = candidates.popMin()
if current дальше чем k-й элемент nearest
break
for v : смежные с current вершины
if !visited.contains(v)
candidates.add(v)
visited.add(v)
tempNearest.add(v)
result.addAll(tempNearest)
return k первых вершин из nearest
Очевидный недостаток этого алгоритма — опасность свалиться в локальный минимум.