Виды ансамблей

Ансамбль

Ансамбль алгоритмов (методов) — метод, который использует несколько обучающих алгоритмов с целью получения лучшей эффективности прогнозирования, чем можно было бы получить от каждого обучающего алгоритма по отдельности.

Рассмотрим задачу классификации на K классов: [math]Y = \{1, 2, ..., K\}[/math]
Пусть имеется M классификатор ("экспертов"): [math] f_1, f_2, ..., f_M [/math]
[math] f_m : X \leftarrow Y, f_m \in F, m = (1 ... M) [/math]

Тогда давайте посмотрим новый классификатор на основе данных:

Простое голосование: [math] f(x) = \max \limits_{k = 1 .. K} \sum \limits_{i = 1}^M I(f_i(x) = k) [/math]
Взвешенное голосование: [math] f(x) = \max \limits_{k = 1 .. K} \sum \limits_{i = 1}^M \alpha_i I(f_i(x) = k), \sum \limits_i \alpha_i = 1, \alpha_i \gt 0[/math]

Теорема Кондорсе о присяжных

Теорема:

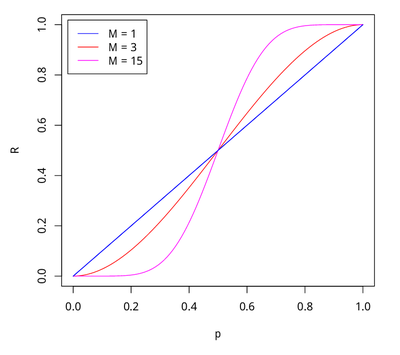
Если каждый член жюри присяжных имеет независимое мнение, и если вероятность правильного решения члена жюри больше 0.5, то тогда вероятность правильного решения присяжных в целом возрастает с увеличением количества членов жюри, и стремиться к единице. Если же вероятность быть правым у каждого из членов жюри меньше 0.5, то вероятность принятия правильного решения присяжными в целом монотонно уменьшается и стремится к нулю с увеличением количества присяжных.

Пусть [math]M[/math] — количество присяжный, [math]p[/math] — вероятность правильного решения одного эксперта, [math]R[/math] — вероятность правильного решения всего жюри, [math]m[/math] — минимальное большинство членов жюри [math] = \lfloor \frac N 2 \rfloor + 1 [/math]

Тогда [math] R = \sum \limits_{i = m}^M C_M^i p ^ i (1 - p) ^ {M - i} [/math]

Вероятность правильного решения всего жюри в зависимости от вероятности правильного решения одного жюри при разном количестве экспертов

Бэггинг

Пусть имеется выборка [math]X[/math] размера [math]N[/math]. Количество классификаторов [math]M[/math]

Для алгоритма нам понадобится метод бутстрэпа (англ. bootstrap):

   Равномерно возьмем из выборки [math]N[/math] объектов с возвращением. Это означает, что мы будем [math]N[/math] раз равновероятно выбирать произвольный объект выборки, причем каждый раз мы выбираем из всех исходных [math]N[/math] объектов. Отметим, что из-за возвращения среди них окажутся повторы. 
Обозначим новую выборку через [math]X_1[/math]. Повторяя процедуру [math]M[/math] раз, сгенерируем [math]M[/math] подвыборок [math]X_1 ... X_M[/math]. Теперь мы имеем достаточно большое число выборок и можем оценивать различные статистики исходного распределения.

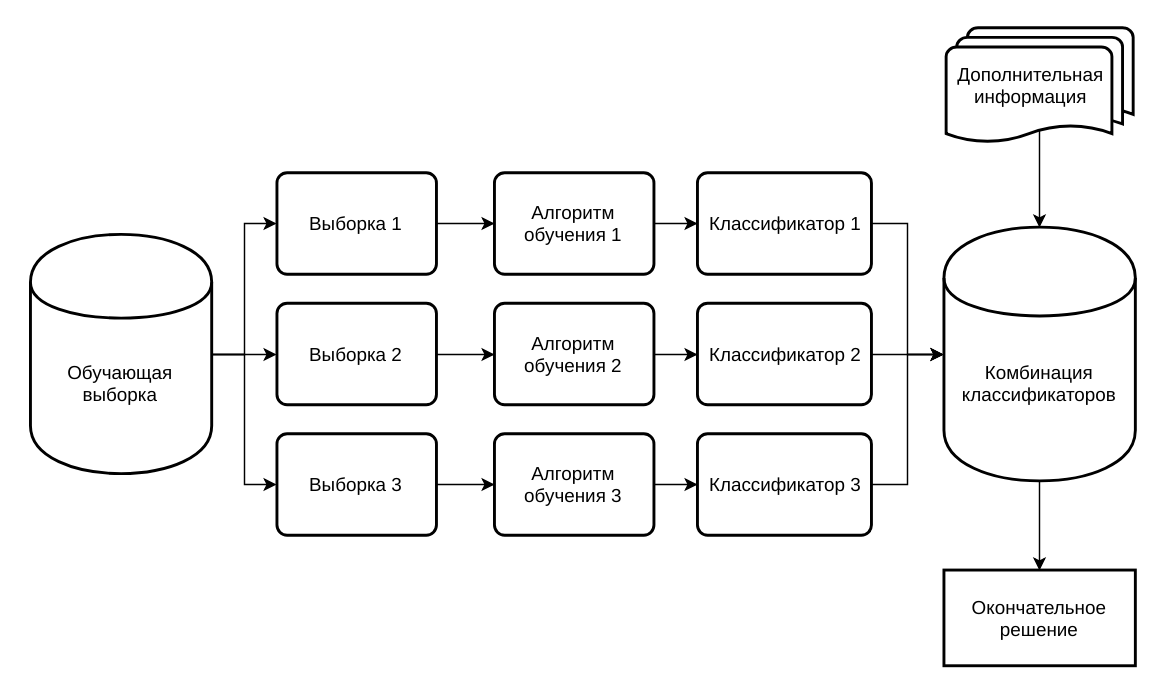
Алгоритм классификации в технологии бэггинг на подпространствах:

• Генерируется с помощью бутстрэпа M выборок размера N для каждого классификатора.
• Производится независимое обучения каждого элементарного классификатора (каждого алгоритма, определенного на своем подпространстве).
• Производится классификация основной выборки на каждом из подпространств (также независимо).
• Принимается окончательное решение о принадлежности объекта одному из классов. Это можно сделать несколькими разными способами, подробнее описано ниже.

Окончательное решение о принадлежности объекта классу может приниматься, например, одним из следующих методов:

• Консенсус: если все элементарные классификаторы присвоили объекту одну и ту же метку, то относим объект к выбранному классу.
• Простое большинство: консенсус достижим очень редко, поэтому чаще всего используют метод простого большинства. Здесь объекту присваивается метка того класса, который определило для него большинство элементарных классификаторов.
• Взвешивание классификаторов: если классификаторов четное количество, то голосов может получиться поровну, еще возможно, что для эксперты одна из групп параметров важна в большей степени, тогда прибегают к взвешиванию классификаторов. То есть при голосовании голос классификатора умножается на его вес.

Рассмотрим задачу регрессии с базовыми алгоритмами [math]b_1, b_2, ..., b_m[/math]. Предположим, что существует истинная функция ответа для всех объектов y(x), а также задано распределение p(x) на объектах. В этом случае мы можем записать ошибку каждой функции регрессии:

[math] \epsilon_i(x) = b_i(x) - y(x), y = 1, ..., n [/math]

и записать матожидание среднеквадратичной ошибки:

[math]E_x(b_i(x) - y(x))^2 = E_x \epsilon_i^2(x) [/math]

Средняя ошибка построенных функций регрессии имеет вид:

[math]E_1 = \frac 1 n E_x \sum \limits_{i = 1}^n \epsilon_i^2(x) [/math]

Предположим, что ошибки несмещены и некоррелированы:

[math] E_x\epsilon_i(x) = 0, E_x\epsilon_i(x)\epsilon_j(x) = 0, i ≠ j [/math]

Построим теперь новую функцию регрессии, которая будет усреднять ответы построенных нами функций:

[math] a(x) = \frac 1 n \sum \limits_{i = 1}^n b_i(x) [/math]

Найдем ее среднеквадратичную ошибку:

[math] E_n = E_x(\frac 1 n \sum \limits_{i = 1}^n (b_i(x) - y(x))^2 = E_x(\frac 1 n \sum \limits_{i = 1}^n \epsilon_i)^2 = \frac 1 {n^2} E_x(\sum \limits_{i = 1}^n \epsilon_i^2(x) + \sum \limits_{i ≠ j} \epsilon_i(x)\epsilon_j(x)) = \frac 1 n E_1 [/math]

Таким образом, усреднение ответов позволило уменьшить средний квадрат ошибки в [math]n[/math] раз

Бустинг

Бустинг (англ. boosting — улучшение) — это процедура последовательного построения композиции алгоритмов машинного обучения, когда каждый следующий алгоритм стремится компенсировать недостатки композиции всех предыдущих алгоритмов. Бустинг представляет собой жадный алгоритм построения композиции алгоритмов

AdaBoost

Алгоритм AdaBoost (сокр. от adaptive boosting) — алгоритм машинного обучения, предложенный Йоавом Фройндом (Yoav Freund) и Робертом Шапиром (Robert Schapire). Является мета-алгоритмом, в процессе обучения строит композицию из базовых алгоритмов обучения для улучшения их эффективности. AdaBoost является алгоритмом адаптивного бустинга в том смысле, что каждый следующий классификатор строится по объектам, которые плохо классифицируются предыдущими классификаторами.

AdaBoost вызывает слабый классификатор в цикле. После каждого вызова обновляется распределение весов, которые отвечают важности каждого из объектов обучающего множества для классификации. На каждой итерации веса каждого неверно классифицированного объекта возрастают, таким образом новый классификатор «фокусирует своё внимание» на этих объектах.

Достоинства

Хорошая обобщающая способность. В реальных задачах (не всегда, но часто) удаётся строить композиции, превосходящие по качеству базовые алгоритмы. Обобщающая способность может улучшаться (в некоторых задачах) по мере увеличения числа базовых алгоритмов.

Простота реализации.

Собственные накладные расходы бустинга невелики. Время построения композиции практически полностью определяется временем обучения базовых алгоритмов.

Возможность идентифицировать объекты, являющиеся шумовыми выбросами. Недостатки

AdaBoost склонен к переобучению при наличии значительного уровня шума в данных. Экспоненциальная функция потерь слишком сильно увеличивает веса наиболее трудных объектов, на которых ошибаются многие базовые алгоритмы. Однако именно эти объекты чаще всего оказываются шумовыми выбросами. В результате AdaBoost начинает настраиваться на шум, что ведёт к переобучению. Проблема решается путём удаления выбросов или применения менее агрессивных функций потерь.

AdaBoost требует достаточно длинных обучающих выборок. Другие методы линейной коррекции, в частности, бэггинг, способны строить алгоритмы сопоставимого качества по меньшим выборкам данных.

Жадная стратегия последовательного добавления приводит к построению неоптимального набора базовых алгоритмов. Для улучшения композиции можно периодически возвращаться к ранее построенным алгоритмам и обучать их заново. Для улучшения коэффициентов можно оптимизировать их ещё раз по окончании процесса бустинга с помощью какого-нибудь стандартного метода построения линейной разделяющей поверхности. Рекомендуется использовать для этой цели SVM (машины опорных векторов).

Бустинг может приводить к построению громоздких композиций, состоящих из сотен алгоритмов. Такие композиции исключают возможность содержательной интерпретации, требуют больших объёмов памяти для хранения базовых алгоритмов и существенных затрат времени на вычисление классификаций.

Примеры кода

Инициализация

   from pydataset import data
   
   #Считаем данные The Boston Housing Dataset
   df = data('Housing')

   #Проверим данные
   df.head().values
   array([[42000.0, 5850, 3, 1, 2, 'yes', 'no', 'yes', 'no', 'no', 1, 'no'],
          [38500.0, 4000, 2, 1, 1, 'yes', 'no', 'no', 'no', 'no', 0, 'no'],
          [49500.0, 3060, 3, 1, 1, 'yes', 'no', 'no', 'no', 'no', 0, 'no'], ...

   # Создадим словарь для слов 'no', 'yes'
   d = dict(zip(['no', 'yes'], range(0,2)))
   for i in zip(df.dtypes.index, df.dtypes):
       if str(i[1]) == 'object':
           df[i[0]] = df[i[0]].map(d)
   df[‘price’] = pd.qcut(df[‘price’], 3, labels=[‘0’, ‘1’, ‘2’]).cat.codes
   
   # Разделим множество на два
   y = df['price'] 
   X = df.drop('price', 1)

Бэггинг

   # Импорты классификаторов
   from sklearn.model_selection import cross_val_score
   from sklearn.ensemble import BaggingClassifier, ExtraTreesClassifier, RandomForestClassifier
   from sklearn.neighbors import KNeighborsClassifier
   from sklearn.linear_model import RidgeClassifier
   from sklearn.svm import SVC
   
   seed = 1075
   np.random.seed(seed)
   # Инициализуруем классификаторы
   rf = RandomForestClassifier()
   et = ExtraTreesClassifier()
   knn = KNeighborsClassifier()
   svc = SVC()
   rg = RidgeClassifier()
   clf_array = [rf, et, knn, svc, rg]
   
   for clf in clf_array:
       vanilla_scores = cross_val_score(clf, X, y, cv=10, n_jobs=-1)
       bagging_clf = BaggingClassifier(clf, max_samples=0.4, max_features=10, random_state=seed)
       bagging_scores = cross_val_score(bagging_clf, X, y, cv=10, n_jobs=-1)
       print "Mean of: {1:.3f}, std: (+/-) {2:.3f [{0}]"  
                          .format(clf.__class__.__name__, 
                          vanilla_scores.mean(), vanilla_scores.std())
       print "Mean of: {1:.3f}, std: (+/-) {2:.3f} [Bagging {0}]\n"
                          .format(clf.__class__.__name__, 
                           bagging_scores.mean(), bagging_scores.std())

   #Результат
   Mean of: 0.632, std: (+/-) 0.081 [RandomForestClassifier]
   Mean of: 0.639, std: (+/-) 0.069 [Bagging RandomForestClassifier]
   
   Mean of: 0.636, std: (+/-) 0.080 [ExtraTreesClassifier]
   Mean of: 0.654, std: (+/-) 0.073 [Bagging ExtraTreesClassifier]
   
   Mean of: 0.500, std: (+/-) 0.086 [KNeighborsClassifier]
   Mean of: 0.535, std: (+/-) 0.111 [Bagging KNeighborsClassifier]
   
   Mean of: 0.465, std: (+/-) 0.085 [SVC]
   Mean of: 0.535, std: (+/-) 0.083 [Bagging SVC]
   
   Mean of: 0.639, std: (+/-) 0.050 [RidgeClassifier]
   Mean of: 0.597, std: (+/-) 0.045 [Bagging RidgeClassifier]

Бустинг

   ada_boost = AdaBoostClassifier()
   grad_boost = GradientBoostingClassifier()
   xgb_boost = XGBClassifier()
   boost_array = [ada_boost, grad_boost, xgb_boost]
   eclf = EnsembleVoteClassifier(clfs=[ada_boost, grad_boost, xgb_boost], voting='hard')
   
   labels = ['Ada Boost', 'Grad Boost', 'XG Boost', 'Ensemble']
   for clf, label in zip([ada_boost, grad_boost, xgb_boost, eclf], labels):
       scores = cross_val_score(clf, X, y, cv=10, scoring='accuracy')
       print("Mean: {0:.3f}, std: (+/-) {1:.3f} [{2}]".format(scores.mean(), scores.std(), label))

   # Результат
   Mean: 0.641, std: (+/-) 0.082 [Ada Boost]
   Mean: 0.654, std: (+/-) 0.113 [Grad Boost]
   Mean: 0.663, std: (+/-) 0.101 [XG Boost]
   Mean: 0.667, std: (+/-) 0.105 [Ensemble]

Источники информации

• https://medium.com/@rrfd/boosting-bagging-and-stacking-ensemble-methods-with-sklearn-and-mlens-a455c0c982de
• https://www.cs.toronto.edu/~delve/data/boston/bostonDetail.html