Поиск ближайших соседей с помощью иерархического маленького мира

Иерархический маленький мир (англ. Hierarchical Navigable Small World) — структура данных, позволяющая эффективно находить K почти что ближайших соседей. По своей концепции напоминает список с пропусками.

Маленький мир

Жадный поиск ближайшего соседа. Чёрные ребра — короткие связи с ближайшими соседями, красные рёбра — длинные связи, обеспечивающие малое мат. ожидание длины пути. Оригинал

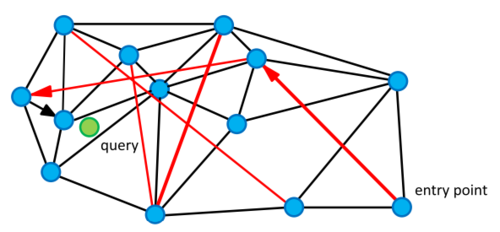
Маленький мир (англ. Small World) — граф, в котором мат. ожидание кратчайшего пути между двумя случайно выбранными вершинами растёт пропорционально [math]\log{N}[/math]. Но при этом средняя степень вершины мала.

Для маленького мира на точках в Евклидовом пространстве жадный поиск K ближайших соседей будет выглядеть так:

knn(V, E, request, m, k):
    W = [math]\emptyset[/math]  // Ближайшие к q вершины. 
    C = [math]\emptyset[/math]  // Вершины, которые предстоит посетить. 
    V = [math]\emptyset[/math]  // Посещённые вершины. 
    for i = 1 to m
        C = С [math]\bigcup[/math] [math]random_v[/math] v [math]\in[/math] G
        TN = [math]\emptyset[/math]  // Ближайшие вершины в этом проходе.
        while true
            u = {q1 | [math]\forall[/math] q2 [math]\in[/math] C, |q - q1| <= |q - q2|} // Ближайшая к q вершина из C 
            C = C [math]\setminus[/math] u
            if u дальше чем k-й элемент W
                break
            for e: (u, e) in G
                if e [math]{\notin}[/math] V
                    C = C [math]\bigcup[/math] e
                    V = V [math]\bigcup[/math] e
                    TN = TN [math]\bigcup[/math] e
        W = W [math]\bigcup[/math] TN
    return k ближайших к q вершин из W

Очевидный недостаток этого алгоритма — опасность свалиться в локальный минимум, остановившись в каком-то кластере. С увеличением числа m, вероятность такого застревания экспоненциально падает.

Описание структуры

Иерархический Маленький мир (англ. Hierarchical Navigable Small World) — слоистая структура графов. На нулевом слое представлены все N вершин из исходной выборки. Вершина, присутствующая на уровне L так же присутствует на уровне L + 1 с вероятностью P. Т.е. кол-во слоёв растет как [math]O(\log N)[/math]. Количество соседей каждой вершины на каждом уровне ограниченно константой, что позволяет делать запросы на добавление и удаление вершины за [math]O(\log N)[/math].

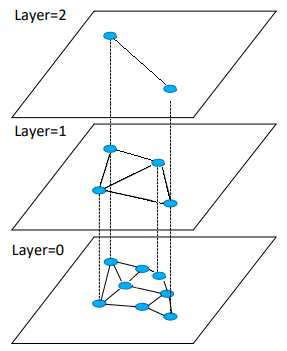Иерархический маленький мир. Источник

Операции над структурой

Поиск ближайших соседей в слое

Жадно идём по уровню в сторону запроса.

searchLayer(q, ep, ef, layer):
    // Входные данные: иерархия графов hnsw, запрос q, входные точки ep, искомое количество ближайших соседей ef, номер слоя layer.
    // Возвращает: ef ближайших соседей q в слое layer.
    W = [math]\emptyset[/math]  // Ближайшие к q вершины. 
    C = [math]\emptyset[/math]  // Вершины, которые предстоит посетить. 
    V = [math]\emptyset[/math]  // Посещённые вершины. 
    while C != [math]\emptyset[/math]
        u = {q1 | [math]\forall[/math] q2 [math]\in[/math] C, |q - q1| <= |q - q2|} // Ближайшая к q вершина из C. 
        f = {q1 | [math]\forall[/math] q2 [math]\in[/math] W, |q - q1| >= |q - q2|} // Самая дальняя от q вершина из W. 
        if |u - q| > |f - q|
            break // Мы в локальном минимуме. 
        for e : (u, e) in G
            if e [math]{\notin}[/math] V
                V = V [math]\bigcup[/math] e
                f = {q1 | [math]\forall[/math] q2 [math]\in[/math] W, |q - q1| >= |q - q2|} // Самая дальняя от q вершина из W. 
                if |e - q| < |f - q| or |W| < ef
                    C = C [math]\bigcup[/math] e
                    W = W [math]\bigcup[/math] e
                    if |W| > ef
                        W = W \ f
    return W

Поиск ближайших соседей во всей структуре

Жадный поиск вершины. Оригинал

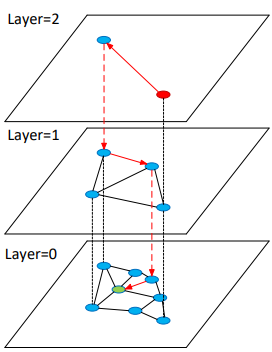
Жадно ищем ближайшего соседа на каждом уровне, кроме 0. Когда находим, спускаемся через него на уровень ниже. На нулевом уровне жадно ищем k ближайших соседей.

knn(hnsw, q, k, ef):
    // Входные данные: иерархия графов hnsw, запрос q, искомое количество ближайших соседей  K, количество кандидатов при поиске ef
    // Возвращает: k ближайших соседей q
    W = [math]\emptyset[/math]  // ближайшие к q вершины 
    mL = |hnsw| - 1
    ep = [math]random_v[/math] v [math]\in[/math] hnsw[mL]
    for level = mL to 1
        W = searchLayer(hnsw, q, ep, ef=1, level) // На каждом уровне, кроме нижнего мы ищем всего одну ближайшую вершину. 
        ep = W
    W = searchLayer(hnsw, q, ep, ef, lc=0)
    return k ближайших к q вершин из W

Вставка элемента

Случайным образом выбираем максимальный слой, на котором представлена q. Жадно ищем M ближайших вершин к q на каждом уровне, на котором она представлена; добавляем связи q с ними; удаляем лишние связи у новообразовавшихся соседей.

insert(hnsw, q, m, mMax, ef, mL):
    // Входные данные: иерархия графов hnsw, запрос на добавление q, желаемое количество связей m, максимальное количество связей вершины 
    //       на одном слое mMax, количество кандидатов при поиске ef, коэффициент выбора высоты mL. 
    // Возвращает: hnsw с вставленным элементом q. 
    W = [math]\emptyset[/math]  // ближайшие к q вершины 
    mL = |hnsw| - 1
    ep = [math]random_v[/math] v [math]\in[/math] hnsw[mL]
    qL = -ln(rand(eps, 1.0)) * mL // Верхний слой для вершины q. 
    for level = mL to qL + 1
        W = searchLayer(q, ep, ef=1, level)
        ep = W
    for level = min(mL, qL) to 0
        W = searchLayer(q, ep, ef, level)
        neighbours = M ближайших к q вершин из W
        for n [math]\in[/math] neighbours:
            hnsw[level] = hnsw[level] [math]\bigcup[/math] (n, q)
            hnsw[level] = hnsw[level] [math]\bigcup[/math] (q, n)
            // Убираем лишние связи, если требуется. 
            nNeighbours = {v| (v, n) in hnsw[level]}
            if nNeighbours.Count() > mMax
                // Самая дальняя от n вершина, смежняя с ней. 
                v = {q1 | (q2, n) [math]\in[/math] nNeighbours & [math]\forall[/math]q2 [math]\in[/math] hnsw[level], |q - q1| >= |q - q2|}
                hnsw[level] = hnsw[level] [math]\setminus[/math] (n, v)
                hnsw[level] = hnsw[level] [math]\setminus[/math] (v, n)
        ep = W
    if qL > mL
        for level = mL to qL
            hnsw.append({q, {}})

См. также

Метрический классификатор и метод ближайших соседей
Иерархическая кластеризация

Источники информации

Статья на википедии о маленьких мирах