Сведение задачи о назначениях к задаче о потоке минимальной стоимости — различия между версиями
| Строка 4: | Строка 4: | ||
== Сведение к задаче о потоке минимальной стоимости == | == Сведение к задаче о потоке минимальной стоимости == | ||
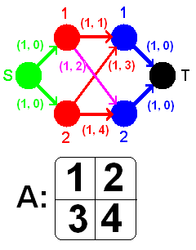
| + | [[Файл:pic.PNG|thumb|right|275x250px|Пример построенного графа для матрицы А]] | ||
Построим двудольный граф <tex>G</tex> следующим образом: | Построим двудольный граф <tex>G</tex> следующим образом: | ||
* Имеется исток <tex>S</tex> и сток <tex>T</tex>. | * Имеется исток <tex>S</tex> и сток <tex>T</tex>. | ||
Версия 00:40, 16 января 2011
Содержание
Постановка задачи
- Дана квадратная матрица . Нужно выбрать в ней элементов так, чтобы в каждой строке и столбце был выбран только один элемент, а сумма значений этих элементов была наименьшей.
- Имеется заказов и станков. Про каждый заказ известна стоимость его изготовления на каждом станке. На каждом станке можно выполнять только один заказ. Требуется распределить все заказы по станкам так, чтобы минимизировать суммарную стоимость.
Сведение к задаче о потоке минимальной стоимости
Построим двудольный граф следующим образом:
- Имеется исток и сток .
- В первой доле находятся вершин, соответствующие строкам матрицы или заказам.
- Во второй вершин, соответствующие столбцам матрицы или станкам.
- Между каждой вершиной первой доли и каждой вершиной второй доли проведём ребро с пропускной способностью 1 и стоимостью .
- От истока проведём рёбра ко всем вершинам первой доли с пропускной способностью 1 и стоимостью 0.
- От каждой вершины второй доли к стоку проведём ребро с пропускной способностью 1 и стоимостью 0.
Найдём в полученном графе максимальный поток минимальной стоимости.
Понятно, что величина потока будет равна . Заметим, что для каждой вершины из первой доли найдётся только одна вершина из второй доли, такая, что поток . Поскольку найденный поток имеет минимальную стоимость, то сумма стоимостей выбранных рёбер будет наименьшей из возможных. Поэтому, это взаимно однозначное соответствие между вершинами первой доли и вершинами второй доли является решением задачи.
Асимптотика
Очевидно, асимптотика этого решения составляет .