(Метки: правка с мобильного устройства, правка из мобильной версии) |
|
| Строка 76: |
Строка 76: |
| | Построим левое порождение цепочки <tex>\omega</tex> следующим образом: | | Построим левое порождение цепочки <tex>\omega</tex> следующим образом: |
| | :Начнем с шага <tex>A \Rightarrow_{lm} X_1X_2\dots X_k</tex>. | | :Начнем с шага <tex>A \Rightarrow_{lm} X_1X_2\dots X_k</tex>. |
| − | :Затем для <tex>i = 1, 2, \dots, k</tex> покажем, что имеет место следующее порождение: <tex>A \Rightarrow^{*}_{lm} \omega_1\omega_2\dots\omega_iX_{i+1}X_{i+2}\dots X_k</tex> | + | :Затем для <tex>i = 1, 2, \dots, k \ </tex> покажем, что имеет место следующее порождение: <tex>A \Rightarrow^{*}_{lm} \omega_1\omega_2\dots\omega_iX_{i+1}X_{i+2}\dots X_k</tex> |
| | | | |
| | Данное доказательство использует в действительности еще одну индукцию, на этот раз по <tex>i</tex>. | | Данное доказательство использует в действительности еще одну индукцию, на этот раз по <tex>i</tex>. |
Версия 17:39, 14 мая 2019
Основные определения
| Определение: |
| Контекстно-свободной грамматикой (англ. сontext-free grammar) называется грамматика, у которой в левых частях всех правил стоят только одиночные нетерминалы. |
| Определение: |
| Контекстно-свободный язык (англ. context-free language) — язык, задаваемый контекстно-свободной грамматикой. |
Лево- и правосторонний вывод слова
| Определение: |
| Выводом слова (англ. derivation of a word) [math]\alpha[/math] называется последовательность строк, состоящих из терминалов и нетерминалов. Первая строка последовательности состоит из одного стартового нетерминала. Каждая последующая строка получена из предыдущей путем замены любого нетерминала по одному (любому) из правил, а последней строкой в последовательности является слово [math]\alpha[/math]. |
Пример:
Рассмотрим грамматику, выводящую все правильные скобочные последовательности.
- [math]"("[/math] и [math]")"[/math] — терминальные символы
- [math]S[/math] — стартовый нетерминал
Правила:
- [math]S\rightarrow (S)S[/math]
- [math]S\rightarrow S(S)[/math]
- [math]S\rightarrow \varepsilon[/math]
Выведем слово [math]"(()(()))()"[/math]:
[math]\boldsymbol{S}\Rightarrow (S)\boldsymbol{S} \Rightarrow (S)(\boldsymbol{S})S\Rightarrow(S)()\boldsymbol{S}\Rightarrow(\boldsymbol{S})()\Rightarrow(\boldsymbol{S}(S))()\Rightarrow(S(S)(\boldsymbol{S}))()\Rightarrow(S(S)(\boldsymbol{S}(S)))()\Rightarrow (S(\boldsymbol{S})((S)))()\Rightarrow(\boldsymbol{S}()((S)))()\Rightarrow(()((\boldsymbol{S})))()\Rightarrow(()(()))()[/math]
| Определение: |
| Левосторонним выводом слова (англ. leftmost derivation) [math]\alpha[/math] называется такой вывод слова [math]\alpha[/math], в котором каждая последующая строка получена из предыдущей путем замены по одному из правил самого левого встречающегося в строке нетерминала. |
| Определение: |
| Правосторонним выводом слова (англ. rightmost derivation) [math]\alpha[/math] называется такой вывод слова [math]\alpha[/math], в котором каждая последующая строка получена из предыдущей путем замены по одному из правил самого правого встречающегося в строке нетерминала. |
Рассмотрим левосторонний вывод скобочной последовательности из примера:
[math]\boldsymbol{S}\Rightarrow (\boldsymbol{S})S \Rightarrow ((\boldsymbol{S})S)S\Rightarrow (()\boldsymbol{S})S\Rightarrow(()\boldsymbol{S}(S))S\Rightarrow(()(\boldsymbol{S}))S\Rightarrow(()(\boldsymbol{S}(S)))S\Rightarrow(()((\boldsymbol{S})))S\Rightarrow(()(()))\boldsymbol{S}\Rightarrow(()(()))(\boldsymbol{S})S\Rightarrow(()(()))()\boldsymbol{S}\Rightarrow(()(()))()[/math]
Дерево разбора
| Определение: |
| Деревом разбора грамматики (англ. parse tree) называется дерево, в вершинах которого записаны терминалы или нетерминалы. Все вершины, помеченные терминалами, являются листьями. Все вершины, помеченные нетерминалами, имеют детей. Дети вершины, в которой записан нетерминал, соответствуют раскрытию нетерминала по одному любому правилу (в левой части которого стоит этот нетерминал) и упорядочены так же, как в правой части этого правила. |
| Определение: |
| Крона дерева разбора (англ. leaves of the parse tree) — множество терминальных символов, упорядоченное в соответствии с номерами их достижения при обходе дерева в глубину из корня. Крона дерева разбора представляет из себя слово языка, которое выводит это дерево. |
Построим дерево разбора скобочной последовательности из примера.

| Теорема: |
Пусть [math]\Gamma = \langle \Sigma, N, S, P \rangle[/math] — КС-грамматика. Предположим, что существует дерево разбора с корнем, отмеченным [math]A[/math], и кроной [math]\omega[/math], где [math]\omega \in N^{*}[/math]. Тогда в грамматике [math]\Gamma[/math] существует левое порождение [math]A \Rightarrow^{*}_{lm} \omega[/math] |
| Доказательство: |
| [math]\triangleright[/math] |
|
Используем индукцию по высоте дерева.
База: Базисом является высота [math]1[/math], наименьшая из возможных для дерева разбора с терминальной кроной.
- Поскольку это дерево является деревом разбора, [math]A \rightarrow \omega[/math] должно быть продукцией. Таким образом, [math]A \Rightarrow_{lm} \omega[/math] есть одношаговое левое порождение [math]\omega[/math] из [math]A[/math].
Индукционный переход: Существует корень с отметкой [math]A[/math] и сыновьями, отмеченными слева направо [math]X_1X_2 \dots X_k[/math]. Символы [math]X[/math] могут быть как терминалами, так и переменными.
- Если [math]X_i[/math] — терминал, то определим [math]\omega_i[/math] как цепочку, состоящую из одного [math]X_i[/math].
- Если [math]X_i[/math] — переменная, то она должна быть корнем некоторого поддерева с терминальной кроной, которую обозначим [math]\omega_i[/math]. Заметим, что в этом случае высота поддерева меньше [math]n[/math], поэтому к нему применимо предположение индукции. Следовательно, существует левое порождение [math]X_i \Rightarrow^{*}_{lm} \omega_i[/math].
Заметим, что [math]\omega = \omega_1\omega_2 \dots \omega_k[/math].
Построим левое порождение цепочки [math]\omega[/math] следующим образом:
- Начнем с шага [math]A \Rightarrow_{lm} X_1X_2\dots X_k[/math].
- Затем для [math]i = 1, 2, \dots, k \ [/math] покажем, что имеет место следующее порождение: [math]A \Rightarrow^{*}_{lm} \omega_1\omega_2\dots\omega_iX_{i+1}X_{i+2}\dots X_k[/math]
Данное доказательство использует в действительности еще одну индукцию, на этот раз по [math]i[/math].
Для базиса [math]i = 0[/math] мы уже знаем, что [math]A \Rightarrow_{lm} X_1X_2\dots X_k[/math].
Для индукции предположим, что существует следующее порождение: [math]A \Rightarrow^{*}_{lm} \omega_1\omega_2\dots\omega_{i–1}X_iX_{i+1}\dots X_k[/math]
- Если [math]X_i[/math] — терминал, то не делаем ничего, но в дальнейшем рассматриваем [math]X_i[/math] как терминальную цепочку [math]\omega_i[/math]. Таким образом, приходим к существованию следующего порождения. [math]A \Rightarrow^{*}_{lm} \omega_1\omega_2\dots\omega_iX_{i+1}X_{i+2}\dots X_k[/math]
- Если [math]X_i[/math] является переменной, то продолжаем порождением [math]\omega_i[/math] из [math]X_i[/math] в контексте уже построенного порождения. Таким образом, если этим порождением является: [math]X_i \Rightarrow_{lm} \alpha_1 \Rightarrow_{lm} \alpha_2\dots \Rightarrow_{lm} \omega_i[/math], то продолжаем следующими порождениями:
- [math]\omega_1\omega_2\dots\omega_{i–1}X_iX_{i+1}\dots X_k \Rightarrow_{lm}[/math]
- [math]\omega_1\omega_2\dots\omega_{i–1}\alpha_1X_{i+1}\dots X_k \Rightarrow_{lm}[/math]
- [math]\omega_1\omega_2\dots\omega_{i–1}\alpha_2X_{i+1}\dots X_k \Rightarrow_{lm}[/math]
- [math]\dots[/math]
- [math]\omega_1\omega_2\dots\omega_iX_{i+1}X_{i+2}\dots X_k[/math]
Результатом является порождение [math]A \Rightarrow^{*}_{lm} \omega_1\omega_2\dots\omega_iX_{i+1}X_{i+2}\dots X_k[/math].
Когда [math]i = k[/math], результат представляет собой левое порождение [math]\omega[/math] из [math]A[/math]. |
| [math]\triangleleft[/math] |
| Теорема: |
Для каждой грамматики [math]\Gamma = \langle \Sigma, N, S, P \rangle[/math] и [math]\omega[/math] из [math]N^{*}[/math] цепочка [math]\omega[/math] имеет два разных дерева разбора тогда и только тогда, когда [math]\omega[/math] имеет два разных левых порождения из [math]P[/math]. |
| Доказательство: |
| [math]\triangleright[/math] |
|
[math]\Longrightarrow[/math]
- Внимательно рассмотрим построение левого порождения по дереву разбора в доказательстве теоремы. В любом случае, если у двух деревьев разбора впервые появляется узел, в котором применяются различные продукции, левые порождения, которые строятся, также используют разные продукции и, следовательно, являются различными.
[math] \Longleftarrow [/math]
- Хотя мы предварительно не описали непосредственное построение дерева разбора по левому порождению, идея его проста. Начнем построение дерева с корня, отмеченного стартовым символом. Рассмотрим порождение пошагово. На каждом шаге заменяется переменная, и эта переменная будет соответствовать построенному крайнему слева узлу дерева, не имеющему сыновей, но отмеченному этой переменной. По продукции, использованной на этом шаге левого порождения, определим, какие сыновья должны быть у этого узла. Если существуют два разных порождения, то на первом шаге, где они различаются, построенные узлы получат разные списки сыновей, что гарантирует различие деревьев разбора.
|
| [math]\triangleleft[/math] |
Однозначные грамматики
| Определение: |
| Грамматика называется однозначной (англ. unambiguous grammar), если у каждого слова имеется не более одного дерева разбора в этой грамматике. |
| Лемма: |
Пусть [math]\Gamma[/math] — однозначная грамматика. Тогда [math]\forall \omega \in \mathbb{L}(\Gamma)[/math] существует ровно один левосторонний (правосторонний) вывод. |
| Доказательство: |
| [math]\triangleright[/math] |
|
Очевидно, что по дереву разбора однозначно восстанавливается левосторонний(правосторонний) вывод. Поскольку каждое слово из языка выводится только одним деревом разбора, то существует только один левосторонний(правосторонний) вывод этого слова. |
| [math]\triangleleft[/math] |
| Утверждение: |
Грамматика из примера не является однозначной. |
| [math]\triangleright[/math] |
|
Выше уже было построено дерево разбора для слова [math]"(()(()))()"[/math].
Построим еще одно дерево разбора для данного слова.
Например, оно будет выглядеть так:
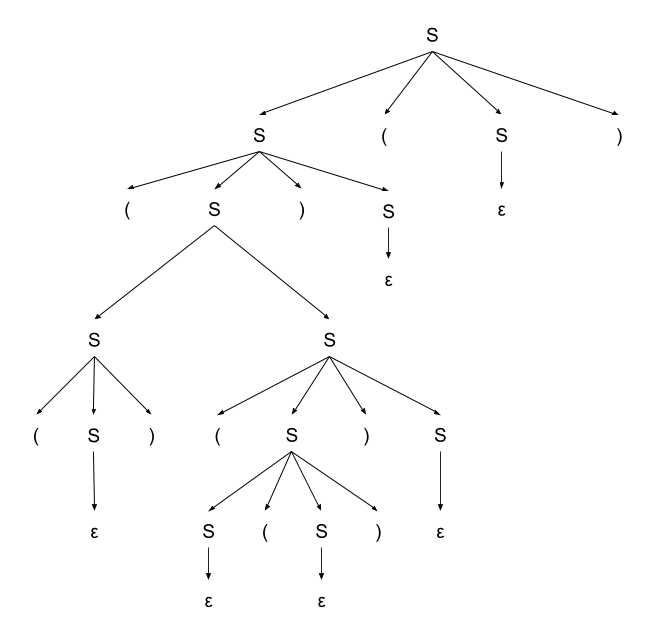
Таким образом, существует слово, у которого есть более одного дерева разбора в данной грамматике [math]\Rightarrow[/math] эта грамматика не является однозначной. |
| [math]\triangleleft[/math] |
| Утверждение: |
Существуют языки, которые можно задать одновременно как однозначными, так и неоднозначными грамматиками. |
| [math]\triangleright[/math] |
|
Для доказательства достаточно привести однозначную грамматику для языка правильных скобочных последовательностей (неоднозначной грамматикой для данного языка является грамматика из примера выше).
Рассмотрим грамматику:
- [math]"("[/math] и [math]")"[/math] — терминальные символы
- [math]S[/math] — стартовый нетерминал
Правила:
- [math]S\rightarrow (S)S[/math]
- [math]S\rightarrow \varepsilon[/math]
Покажем, что эта грамматика однозначна.
Для этого, используя индукцию, докажем, что для любого слова [math]\omega[/math], являющегося правильной скобочной последовательностью, в данной грамматике существует только одно дерево разбора.
База: Если [math]\omega=\varepsilon[/math], то оно выводится только по второму правилу [math]\Rightarrow[/math] для него существует единственное дерево разбора.
Индукционный переход: Пусть [math]\left\vert \omega \right\vert=n[/math] и [math]\forall \upsilon[/math]: [math]\left\vert \upsilon \right\vert \lt n[/math] и [math]\upsilon[/math] — правильная скобочная последовательность, у которой [math]\exists![/math] дерево разбора.
- Найдем в слове [math]\omega[/math] минимальный индекс [math]i \neq 0[/math] такой, что слово [math]\omega[0..i][/math] является правильной скобочной последовательностью. Так как [math]i \neq 0[/math] минимальный, то [math]\omega[0..i]=(\alpha)[/math]. Из того, что [math]\omega[/math] является правильной скобочной последовательностью [math]\Rightarrow[/math] [math]\alpha[/math] и [math]\beta=\omega[i+1..n-1][/math] — правильные скобочные последовательности, при этом [math]\left\vert \alpha \right\vert\lt n[/math] и [math]\left\vert \beta \right\vert\lt n \Rightarrow[/math] по индукционному предположению предположению у [math]\alpha[/math] и [math]\beta[/math] существуют единственные деревья разбора.
- Если мы покажем, что из части [math](S)[/math] первого правила можно вывести только слово [math](\alpha)[/math], то утверждение будет доказано (так как из первой части первого правила выводится [math]\alpha[/math], а из второй только [math]\beta[/math] и для каждого из них по предположению существуют единственные деревья разбора).
- Пусть из [math](S)[/math] была выведена часть слова [math]\omega[0..j]=(\gamma)[/math], где [math]j \lt i[/math], при этом [math]\gamma[/math] является правильной скобочной последовательностью, но тогда как минимальный индекс мы должны были выбрать [math]j[/math], а не [math]i[/math] — противоречие.
- Аналогично из [math](S)[/math] не может быть выведена часть слова [math]\omega[0..j][/math], где [math]j \gt i[/math], потому что тогда [math]\omega[0..i]=(\alpha)[/math] не будет правильной скобочной последовательностью, так как в позиции [math]i-1[/math] баланс скобок будет отрицательный.
- Значит, из [math](S)[/math] была выведена часть слова [math]\omega[0..i] \Rightarrow \omega[/math] имеет единственное дерево разбора [math]\Rightarrow[/math] данная грамматика однозначная.
Таким образом, для языка правильных скобочных последовательностей мы привели пример как однозначной, так и неоднозначной грамматики. |
| [math]\triangleleft[/math] |
Однако, есть КС-языки, для которых не существует однозначных КС-грамматик. Такие языки и грамматики их порождающие называют существенно неоднозначными.
См. также
Источники информации

