Алгоритм вырезания соцветий

Паросочетание в недвудольном графе

Определение:

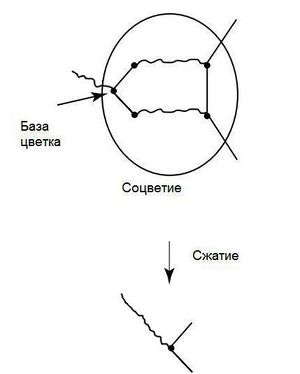
Соцветие [math]B[/math] графа [math]G=(V,E)[/math] - цикл, состоящий из [math]2k + 1[/math] ребер.

Определение:

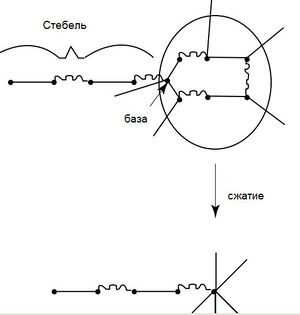
Cжатие соцветия - граф [math]G'[/math], полученный из [math]G[/math] сжатием всего нечётного цикла в одну псевдо-вершину (соответственно, все рёбра, инцидентные вершинам этого цикла, становятся инцидентными псевдо-вершине).

Определение:

База соцветия - вершина соцветия, в которую входит ребро не из данного соцветия.

Теорема Эдмондса

Теорема:

Пусть в графе [math]G[/math] существует соцветие [math]B[/math]. Тогда в [math]G[/math] существует удлиняющий путь тогда и только тогда, когда существует удлиняющий путь в [math]G\setminus B[/math]

Доказательство:

[math]\triangleright[/math]

Пусть граф [math]G'[/math] - граф, полученный [math]G[/math] сжатием соцветия [math]B[/math] в псевдо-вершину [math]B'[/math]. Заметим, что достаточно рассматривать случай, когда база соцветия является свободной вершиной (не принадлежащей паросочетанию). В противном случае в базе соцветия оканчивается чередующийся путь чётной длины, начинающийся в свободной вершине. Прочередовав паросочетание вдоль этого пути, мощность паросочетания не изменится, а база соцветия станет свободной вершиной. [math]\Rightarrow[/math] Пусть путь [math]P[/math] является удлиняющим в графе [math]G[/math]. Если [math]P[/math] не проходит через [math]B[/math], то тогда он будет удлиняющим и в графе [math]G'[/math]. Пусть проходит через [math]B[/math]. Тогда что путь P представляет собой некоторый путь [math]P_1[/math], не проходящий по вершинам [math]B[/math], плюс некоторый путь [math]P_2[/math], проходящий по вершинам [math]B[/math] и, возможно, другим вершинам. Но тогда путь [math]P_1 + B'[/math] будет являться удлиняющим путём в графе [math]G'[/math], что и требовалось доказать. [math]\Leftarrow[/math] Пусть путь [math]P[/math] является удлиняющим путём в графе [math]G'[/math]. Если [math]P[/math] не проходит через [math]B'[/math], то тогда он будет удлиняющим и в графе [math]G[/math]. Рассмотрим отдельно случай, когда [math]P[/math] начинается со сжатого соцветия [math]B'[/math], т.е. имеет вид [math](B', c, ...)[/math]. Тогда в соцветии [math]B[/math] найдётся соответствующая вершина [math]v[/math], которая связана ребром с [math]c[/math]. Заметим, что из базы соцветия всегда найдётся чередующийся путь чётной длины до вершины [math]v[/math]. Учитывая всё вышесказанное, получаем, что путь [math]P_1(b,...v,...c,..)[/math] является увеличивающим путём в графе [math]G[/math]. Пусть теперь путь [math]P[/math] проходит через псевдо-вершину [math]B'[/math], но не начинается и не заканчивается в ней. Тогда в [math]P[/math] есть два ребра, проходящих через [math]B'[/math], пусть это [math](a,B')[/math] и [math](B',c)[/math]. Одно из них обязательно должно принадлежать паросочетанию, однако, так как база цветка не насыщена, а все остальные вершины цикла цветка насыщены рёбрами цикла, то мы приходим к противоречию (это эквивалентно случаю отсутствия ребра из [math]R_-[/math] в [math]L_+[/math]). Таким образом, этот случай просто невозможен. Теорема доказана.

[math]\triangleleft[/math]

Алгоритм вырезания соцветий

Пусть дан произвольный граф [math]G(V, E)[/math] и требуется найти максимальное паросочетание в нём.

Рис. 1

Общая идея

Рис. 2

1. Сжимаем все соцветия
2. Находим паросочетания в полученном графе поиском в глубину/ширину.
3. Разжимаем соцветия, восстанавливая паросочетание.

Пошаговое представление

Алгоритм строит лес(используя поиск в глубину или ширину), содержащий деревья удлиняющих путей, корнями которых являются вершины не из паросочетания.

Разобьем каждое неориентированное ребро [math](w, v)[/math] на два ориентированных ребра [math](w, v)[/math] и [math](v, w)[/math]. Каждое ребро может принимать одно из трех состояний: непосещенное, четное и нечетное. Для каждой вершины из паросочетания [math]v[/math] в [math]mate(v)[/math] будем хранить вершину, смежную [math]v[/math]. Также для каждой вершины [math]v[/math] алгоритм в [math]p(v)[/math] будет хранить родителя в дереве обхода.

Сначала пометим все вершины, включенные в паросочетание, непосещенными, все остальные - четными.

Пока существует удлиняющий путь или пока есть непроверенное ребро из четной вершины [math]v[/math]:

1. Выберем любое непроверенное ребро[math](v, w)[/math] из четной вершины [math]v[/math] и проверяем:
   • Вершина [math]w[/math] нечетное - ничего не делаем. Такая ситуация возникает, когда [math](v, w)[/math] ребро из паросочетания или не из паросочетания
   • Вершина [math]w[/math] включено в паросочетание и непосещенное. Тогда помечаем [math]w[/math] нечетным, а [math]mate(w)[/math] четным. Присваиваем [math]p(w) \gets v[/math], а также [math]p(mate(w)) \gets w[/math]
   • [math]w[/math] четное; вершины [math]w, v[/math] лежат в разных деревьях - нашли удлиняющий путь от корня дерева, содержащего вершину [math]v[/math] до корня дерева, содержащего вершину [math]w[/math].
   • [math]w[/math] четное; вершины [math]w, v[/math] лежат в одном дереве - нашли соцветие. Пусть [math]u[/math] - наименьший общий предок вершин [math]v[/math] и [math]w[/math]. Сожмем соцветие в псевдо-вершину [math]b[/math], [math]p(b) \gets p(u)[/math], а также для каждой вершины [math]x[/math] в соцветии определим [math]p(x) \gets b[/math]

Псевдокод

  Edmonds {
     for [math]u \in V[/math]
     if (вершина u не в паросочетании) {
         int last_v = find_augment_path (u);
         if (last_v != -1)
             выполнить чередование вдоль пути из u в last_v;
     }
  }

  int find_augment_path (root) {
     обход в ширину:
        v = текущая_вершина;
        for [math](v,w) \in E[/math]
            если обнаружили цикл нечётной длины, сжать его
            если пришли в свободную вершину, return
            если пришли в несвободную вершину, то добавить в очередь смежную ей в паросочетании
     return -1;
   }

Оценка сложности

Всего имеется [math]V[/math] итераций, на каждой из которых выполняется обход в ширину за [math]O(E)[/math], кроме того, могут происходить операции сжатия цветков — их может быть [math]O(V)[/math]. Если уметь сжимать соцветие за [math]O(V)[/math], то общая асимптотика алгоритма составит [math]O(V(E + V^2)) = O(V^3)[/math].

Литература

• R. Tarjan Data Structures and Network Algorithms -ISBN 0898711878
• Алгоритм Алгоритм Эдмондса нахождения наибольшего паросочетания в произвольных графах