Матричный умножитель — различия между версиями
Rybak (обсуждение | вклад) (→Определение) |
(→Схемная сложность) |
||
| Строка 15: | Строка 15: | ||
вначале мы суммируем <tex>m_0</tex> и <tex>m_1</tex>, саму сумму занесем в <tex>u_1</tex>, а переносы в <tex>v_1</tex>(в <tex>u_1</tex> и <tex>v_1</tex> будет не более n+1 битов в каждом), затем суммируем числа <tex>u_1</tex>, <tex>v_1</tex>, <tex>m_2</tex> и получаем <tex>u_2</tex>, <tex>v_2</tex>. Так суммируется <tex>u_{i-1}</tex>, <tex>v_{i-1}</tex>, <tex>m_i</tex> для всех i = 2, 3, … , n – 1. В итоге получаем два числа <tex>u_{n-1}</tex> и <tex>v_{i-1}</tex>, которые складываем с помощью [[двоичный каскадный сумматор|двоичного каскадного сумматора]]. | вначале мы суммируем <tex>m_0</tex> и <tex>m_1</tex>, саму сумму занесем в <tex>u_1</tex>, а переносы в <tex>v_1</tex>(в <tex>u_1</tex> и <tex>v_1</tex> будет не более n+1 битов в каждом), затем суммируем числа <tex>u_1</tex>, <tex>v_1</tex>, <tex>m_2</tex> и получаем <tex>u_2</tex>, <tex>v_2</tex>. Так суммируется <tex>u_{i-1}</tex>, <tex>v_{i-1}</tex>, <tex>m_i</tex> для всех i = 2, 3, … , n – 1. В итоге получаем два числа <tex>u_{n-1}</tex> и <tex>v_{i-1}</tex>, которые складываем с помощью [[двоичный каскадный сумматор|двоичного каскадного сумматора]]. | ||
==Схемная сложность== | ==Схемная сложность== | ||
| − | Частичные произведения вычисляются за ''n'' шагов. Сложение с | + | Частичные произведения вычисляются за ''n'' шагов. Сложение с вычислением переносов включает ''n - 1'' шаг. Последнее сложение можно выполнить за ''O(log n)''. <br> |
В итоге суммарное время работы: <br> | В итоге суммарное время работы: <br> | ||
''O(n) + O(n) + O(log n) = O(n)'' <br> | ''O(n) + O(n) + O(log n) = O(n)'' <br> | ||
Версия 02:32, 16 января 2011
Содержание
Определение
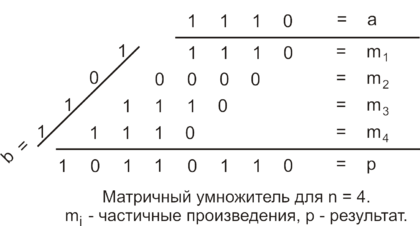
Матричный умножитель — цифровая схема, осуществляющяя умножение двух чисел c помощью суммирования.
Принцип работы
Вычисление частичных произведений
Матричный умножитель вычисляет частичные произведения по формуле:
Суммирование частичных произведений
На этом этапе происходит сложение всех частичных произведений m. Это происходит так: вначале мы суммируем и , саму сумму занесем в , а переносы в (в и будет не более n+1 битов в каждом), затем суммируем числа , , и получаем , . Так суммируется , , для всех i = 2, 3, … , n – 1. В итоге получаем два числа и , которые складываем с помощью двоичного каскадного сумматора.
Схемная сложность
Частичные произведения вычисляются за n шагов. Сложение с вычислением переносов включает n - 1 шаг. Последнее сложение можно выполнить за O(log n).
В итоге суммарное время работы:
O(n) + O(n) + O(log n) = O(n)
Есть и более быстрые способы умножения двух чисел, например умножение с помощью дерева Уоллеса, которое работает O(log n).
Литература
- Кормен Т., Лейзерсон Ч., Ривест Р.. Алгоритмы: построение и анализ = Introduction to Algorithms / Пер. с англ. под ред. А. Шеня. — М.: МЦНМО, 2000. — 960 с. — ISBN 5-900916-37-5