Алгоритм для синхронного порядка

Этот алгоритм берёт систему с асинхронным(?) порядком и начинает гарантировать в ней синхронный порядок.

Алгоритм для синхронного порядка основан на иерархии процессов (точнее, произвольном DAG процессов, отправлять сообщения могут только соединённые ребром), мы рассмотрим полный линейный порядок. Упорядочим процессы по номеру, назовем сообщение большим, если номер отправителя больше номера получателя, и малым иначе. Процесс может быть в активном или пассивном состоянии. Изначально все активны. В пассивном состоянии процесс не может ни отправлять, ни получать сообщения, он их складывает в очередь и ждёт, пока не станет активным.

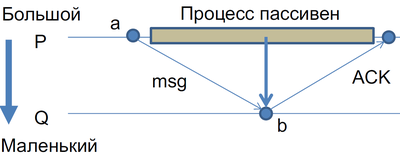
Если процесс хочет отправить большое сообщение, то он его отправляет и ждёт подтверждения. А пока ждёт — становится пассивным.

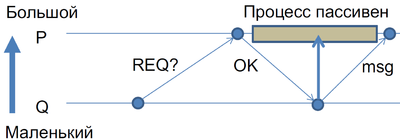
Чтобы отправить сообщение большему процессу [math]P_j[/math], процесс [math]P_i[/math] сначала посылает служебное сообщение, запрос. В ответ [math]P_j[/math] отправляет разрешение; он может сделать это только в активном состоянии. Разрешив, он становится пассивным и остается в этом состоянии, пока не получает сообщение, которое разрешил.

Таким образом, сообщения по факту "передаются" только от больших к маленьким и тогда можно нарисовать стрелочки. Взаимная блокировка наступить не может: мы ждём только меньших процессов, а транзитивность у нас есть и циклов быть не может. Если маленький хочет отправить сообщение большому, то он отсылает запрос и продолжает работать (посылать большие и маленькие сообщения, менять своё состояние). Ничего страшного, что по факту сообщение "отправится" только через какое-то время — с точки зрения процесса оно просто долго было в пути.

Разумеется, надо аккуратно доказать, что функцию $T$ можно придумать. Это делается на странице 200 в Gaarg, там происходит что-то вроде логических часов.