Алгоритмы сэмплирования

Сэмплирование (англ. data sampling) — метод корректировки обучающей выборки с целью балансировки распределения классов в исходном наборе данных. Нужно отличать этот метод от сэмплирования в активном обучении для отбора кандидатов и от сэмплирования в статистике для создания подвыборки с сохранением распределения классов.

Неравномерное распределение может быть следующих типов:

• Недостаточное представление класса в независимой переменной;
• Недостаточное представление класса в зависимой переменной.

Многие модели машинного обучения, например, нейронные сети, дают более надежные прогнозы на основе обучения со сбалансированными данными. Однако некоторые аналитические методы, в частности линейная регрессия и логистическая регрессия, не получают дополнительного преимущества.

Когда в обучающем наборе данных доля примеров некоторого класса слишком мала, такие классы называются миноритарными (англ. minority), другие, со слишком большим количеством представителей, — мажоритарными (англ. majority). Подобные тенденции хорошо заметны в кредитном скоринге, в медицине, в директ-маркетинге.

Следует отметить то, что значимость ошибочной классификации может быть разной. Неверная классификация примеров миноритарного класса, как правило, обходится в разы дороже, чем ошибочная классификация примеров мажоритарного класса. Например, при классификации людей, обследованных в больнице, на больных раком (миноритарный класс) и здоровых (мажоритарный класс) лучше будет отправить на дополнительное обследование здоровых пациентов, чем пропустить людей с раком.

Стратегии сэмплирования

• Cубдискретизация (англ. under-sampling) — удаление некоторого количества примеров мажоритарного класса.
• Передискретизации (англ. over-sampling) — увеличение количества примеров миноритарного класса.
• Комбинирование (англ. сombining over- and under-sampling) — последовательное применение субдискретизации и передискретизации.
• Ансамбль сбалансированных наборов (англ. ensemble balanced sets) — использование встроенных методов сэмплирования в процессе построения ансамблей классификаторов.

Также все методы можно разделить на две группы: случайные (недетерминированные) и специальные (детерминированные).

Примеры алгоритмов

Рис. [math]1[/math]. Случайное удаление примеров мажоритарного класса

Cубдискретизация (удаление примеров мажоритарного класса)

Случайное удаление примеров мажоритарного класса (англ. Random Undersampling)

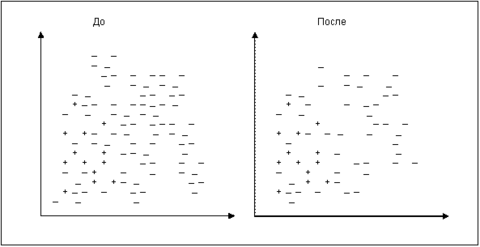
Это самый простой алгоритм. Рассчитывается число [math]K[/math] – количество мажоритарных примеров, которое необходимо удалить для достижения требуемого уровня соотношения различных классов. Затем случайным образом выбираются K мажоритарных примеров и удаляются. На рис. [math]1[/math] изображены примеры некоторого набора данных в двумерном пространстве признаков до и после использования алгоритма.

Поиск связей Томека (англ. Tomek Links)

Рис. [math]2[/math]. Удаление мажоритарных примеров, участвующих в связях Томека

Пусть примеры [math]E_i[/math] и [math]E_j[/math] принадлежат к различным классам, [math]d(E_i,E_j)[/math] – расстояние между указанными примерами. Пара [math](E_i,E_j)[/math] называется связью Томека, если не найдется ни одного примера [math]E_l[/math] такого, что будет справедлива совокупность неравенств:

[math] \begin{cases} d(E_i,E_l)\lt d(E_i,E_j),\\ d(E_j,E_l)\lt d(E_i,E_j) \end{cases} [/math]

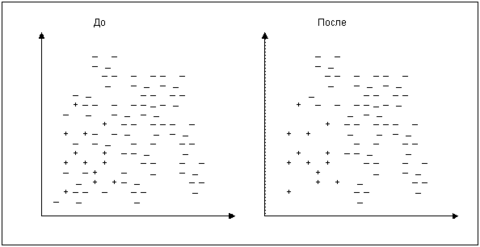
Согласно данному подходу, все мажоритарные записи, входящие в связи Томека, должны быть удалены из набора данных. Этот способ хорошо удаляет записи, которые можно рассматривать в качестве «зашумляющих». На рис. [math]2[/math] визуально показан набор данных в двумерном пространстве признаков до и после применения стратегии поиска связей Томека.

Правило сосредоточенного ближайшего соседа (англ. Condensed Nearest Neighbor Rule)

Рис. [math]3[/math]. Удаление примеров мажоритарного класса правилом сосредоточенного ближайшего соседа

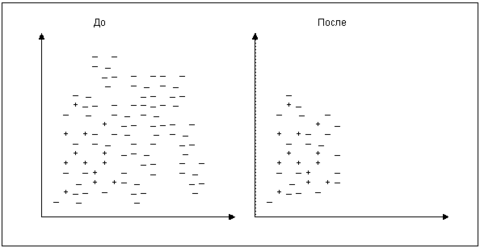
Пусть [math]L[/math] – исходный набор данных. Из него выбираются все миноритарные примеры и (случайным образом) один мажоритарный. Обозначим это множество как [math]S[/math]. Все примеры из [math]L[/math] классифицируются по правилу одного ближайшего соседа. Записи, получившие ошибочную метку, добавляются во множество [math]S[/math] (рис. [math]3[/math]). Таким образом, мы будем учить классификатор находить отличие между похожими примерами, но принадлежащими к разным классам.

Односторонний сэмплинг (англ. One-side sampling, one-sided selection)

Главная идея этой стратегии – это последовательное сочетание предыдущих двух, рассмотренных выше. Для этого на первом шаге применяется правило сосредоточенного ближайшего соседа, а на втором – удаляются все мажоритарные примеры, участвующие в связях Томека. Таким образом, удаляются большие «сгустки» мажоритарных примеров, а затем область пространства со скоплением миноритарных очищается от потенциального шума.

Правило «очищающего» соседа (англ. Neighborhood cleaning rule)

Эта стратегия также направлена на то, чтобы удалить те примеры, которые негативно влияют на исход классификации миноритарных классов. Для этого все примеры классифицируются по правилу трех ближайших соседей. Удаляются следующие мажоритарные примеры:

• получившие верную метку класса;
• являющиеся соседями миноритарных примеров, которые были неверно классифицированы.

Дополнительные

• Under-sampling with Cluster Centroids — уменьшает количество примеров мажоритарного класса, заменяя некоторые кластеры примеров мажоритарного класса их представителем (центроидом кластера).
• NearMiss [math](1 \And 2 \And 3)[/math] — удаляет примеры мажоритарного класса, для которых среднее расстояние до ближайших соседей (KNN) миноритарного класса является наименьшим. Также может использоваться расстояние до самых дальних соседей, либо среднее расстояние до всех соседей.
• Edited Nearest Neighbours — удаляет примеры мажоритарного класса, если при классификации методом KNN они определяются как примеры миноритарного класса.
• Neighboorhood Cleaning Rule — улучшение предыдущего алгоритма, в дополнение к удалению неверно классифицируемых примеров мажоритарного классов, удаляются все соседи примеров миноритарного класса, которые влияют на их неправильную классификацию методом KNN.

Передискретизации (увеличение числа примеров миноритарного класса)

Дублирование примеров миноритарного класса (англ. Oversampling)

Самый простой метод – это дублирование примеров миноритарного класса. В зависимости от того, какое соотношение классов необходимо, выбирается количество случайных записей для дублирования.

Рис. [math]4[/math]. Искусственно созданные новые примеры миноритарного класса

SMOTE (англ. Synthetic Minority Oversampling Technique)

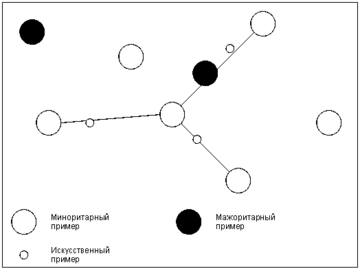
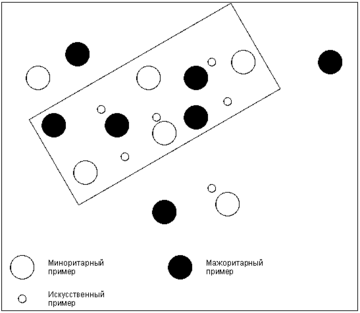
Этот алгоритм основан на идее генерации некоторого количества искусственных примеров, которые были бы похожи на имеющиеся в миноритарном классе, но при этом не дублировали их. Для создания новой записи находят разность [math]d=X_b–X_a[/math], где [math]X_a[/math],[math]X_b[/math] – векторы признаков «соседних» примеров [math]a[/math] и [math]b[/math] из миноритарного класса. Их находят, используя алгоритм ближайшего соседа KNN. В данном случае необходимо и достаточно для примера [math]b[/math] получить набор из [math]k[/math] соседей, из которого в дальнейшем будет выбрана запись [math]b[/math]. Остальные шаги алгоритма KNN не требуются. Далее из [math]d[/math] путем умножения каждого его элемента на случайное число в интервале [math](0, 1)[/math] получают [math]\hat{d}[/math]. Вектор признаков нового примера вычисляется путем сложения [math]X_a[/math] и [math]\hat{d}[/math]. Алгоритм SMOTE позволяет задавать количество записей, которое необходимо искусственно сгенерировать. Степень сходства примеров [math]a[/math] и [math]b[/math] можно регулировать путем изменения числа ближайших соседей [math]k[/math]. На рис. [math]4[/math] схематично изображено то, как в двумерном пространстве признаков могут располагаться искусственно сгенерированные примеры.

Рис. [math]5[/math]. Негативное влияние алгоритма SMOTE

ASMO (англ. Adaptive Synthetic Minority Oversampling)

Рис. [math]6[/math]. Основная идея алгоритма ASMO

Алгоритм SMOTE имеет недостаток в том, что «вслепую» увеличивает плотность примерами в области слабо представленного класса (рис. [math]5[/math]). В случае, если миноритарные примеры равномерно распределены среди мажоритарных и имеют низкую плотность, алгоритм SMOTE только сильнее перемешает классы. В качестве решения данной проблемы был предложен алгоритм адаптивного искусственного увеличения числа примеров миноритарного класса ASMO:

1. Если для каждого [math]i[/math]-ого примера миноритарного класса из [math]k[/math] ближайших соседей [math]g, (g≤k)[/math] принадлежит к мажоритарному, то набор данных считается «рассеянным». В этом случае используют алгоритм ASMO, иначе применяют SMOTE (как правило, [math]g[/math] задают равным [math]20[/math]).
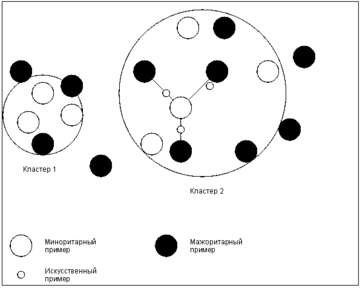
2. Используя только примеры миноритарного класса, выделить несколько кластеров (например, алгоритмом [math]\mathrm{k}[/math]-средних).
3. Сгенерировать искусственные записи в пределах отдельных кластеров на основе всех классов. Для каждого примера миноритарного класса находят [math]m[/math] ближайших соседей, и на основе них (также как в SMOTE) создаются новые записи.

Такая модификация алгоритма SMOTE делает его более адаптивным к различным наборам данных с несбалансированными классами. Общее представление идеи алгоритма показано на рис. [math]6[/math].

Дополнительные

• SMOTENC — в отличие от SMOTE, работает с непрерывными признаками у примеров обучающей выборки.
• Borderline-SMOTE [math](1 \And 2)[/math] — в отличие от SMOTE, для создания новых синтетических примеров используются только примеры на границе классов.
• SVM SMOTE - Support Vectors SMOTE — вариант алгоритма SMOTE, который использует алгоритм SVM для обнаружения примеров, рядом с которыми будут создаваться новые синтетические примеры.

Комбинирование

• SMOTE [math]+[/math] Tomek links
• SMOTE [math]+[/math] ENN

Ансамбль сбалансированных наборов

• Easy Ensemble classifier
• Balanced Random Forest
• Balanced Bagging
• RUSBoost

Реализации

Imbalanced-learn — набор инструментов с открытым исходным кодом на Python, целью которого является предоставление широкого спектра методов для решения проблемы несбалансированного набора данных. На рис. [math]7[/math] представлена таблица реализованных в библиотеке методов.

Пример кода для передискретизации набора данных с использованием SMOTE:

 from sklearn.datasets import make_classification
 from sklearn.decomposition import PCA
 from imblearn.oversampling import SMOTE
                 
 # Создание датасета
 X, y = makeclassification (n_classes=2, weights =[0.1, 0.9],
 n_features=20, n_samples=5000)
 
 Применение SMOTE over-sampling
 sm = SMOTE(ratio=’auto’, kind=’regular’)
 X_resampled , y_resampled=sm.fit_sample(X, y)

Рис. [math]7[/math]. Методы imbalanced-learn

См. также

• Метрический классификатор и метод ближайших соседей
• Байесовская классификация
• Активное обучение
• Виды ансамблей

Источники информации

1. Oversampling and undersampling in data analysis
2. Различные стратегии сэмплинга в условиях несбалансированности классов
3. Lemaître, G. Nogueira, F. Aridas, Ch.K. (2017) Imbalanced-learn: A Python Toolbox to Tackle the Curse of Imbalanced Datasets in Machine Learning, Journal of Machine Learning Research, vol. 18, no. 17, 2017, pp. 1-5.