Подсчет деревьев

Эта статья находится в разработке!

Описание всех используемых далее комбинаторных объектов можно найти в статье "конструирование комбинаторных объектов и их подсчёт".

Бинарные деревья

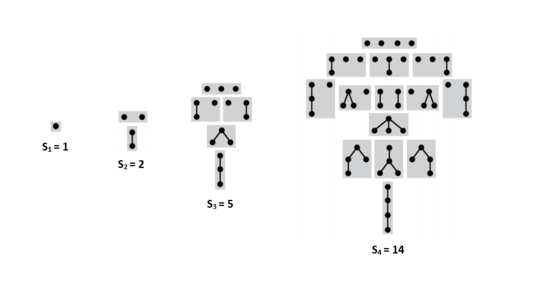
Утверждение:

Число непомеченных бинарных деревьев: [math]T(s) = C_{n}[/math] ([math]n[/math]-ое число Каталана).

[math]\triangleright[/math]

Устройство бинарного дерева в терминах комбинаторных классов выражается следующим образом [math]T = \varepsilon + z\times T\times T[/math]. В терминах производящих функций эта конструкция выглядит следующим образом [math]T(s) = 1 + s{T(s)}^2[/math]. Решением данного уравнения будет [math]T(s) = \frac{1 - \sqrt{1 - 4s}}{2s}[/math]. Тогда: [math]T_{n}={Pair(T, \; T)}_{n-1}=\sum\limits_{i=0}^{n-1}T_{i}T_{n-i-1}=C_{n}[/math], где [math]C_{n}[/math] — [math]n[/math]-ое число Каталана.

[math]\triangleleft[/math]

Утверждение:

Производящая функция числа непомеченных полных бинарных деревьев: [math]T(s) = \frac{1 - \sqrt{1 - 4s^2}}{2s}[/math].

[math]\triangleright[/math]

Устройство бинарного дерева в терминах комбинаторных классов выражается следующим образом [math]T = z + z\times T\times T[/math]. В терминах производящих функций эта конструкция выглядит следующим образом [math]T(s) = s + s{T(s)}^2[/math]. Решением данного уравнения будет [math]T(s) = \frac{1 - \sqrt{1 - 4s^2}}{2s}[/math].

[math]\triangleleft[/math]

Подвешенные непомеченные деревьея с порядком на детях

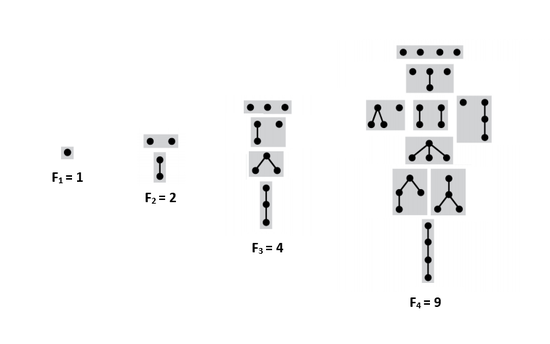
Пусть [math]T_{n}[/math] — количество таких деревьев с [math]n[/math] вершинами. [math]S=Seq(A)[/math] — множество всех последовательностей из данных деревьев. [math]S_{n}[/math] — количество последовательностей с суммарным количество вершин [math]n[/math]. Чтобы получить дерево из [math]n[/math] вершин, достаточно взять [math]1[/math] вершину, и подвесить к ней последовательность деревьев с суммарным количеством вершин [math]n-1[/math]. Тогда:

[math]T_{n}=S_{n-1}[/math].

[math]S_{n}=\sum\limits_{i=1}^{n} T_{i} S_{n-i}=\sum\limits_{i=1}^{n} S_{i-1} S_{n-i}=\sum\limits_{i=0}^{n-1} S_{i} S_{n-i-1}=C_{n}[/math], где [math]C_{n}[/math] — [math]n[/math]-ое число Каталана.

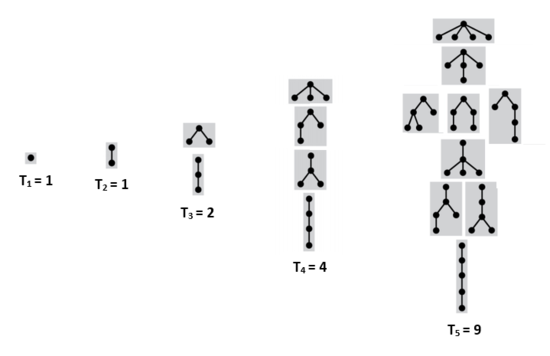
Подвешенные непомеченные деревья без порядка на детях

Пусть [math]T_{n}[/math] — количество таких деревьев с [math]n[/math] вершинами. [math]F=MSet(T)[/math] — множество всех лесов из данных деревьев, так как лес можно интерпретировать как мультимножество из деревьев. [math]F_{n}=f_{n,n}[/math] — количество лесов с суммарным количество вершин [math]n[/math]. [math]f_{n, k}[/math] — количество таких лесов из [math]n[/math] вершин, что деревья в них содержат не более чем [math]k[/math] вершин. Чтобы получить дерево из [math]n[/math] вершин, достаточно взять [math]1[/math] вершину и подвесить к ней лес деревьев с суммарным количеством вершин [math]n-1[/math]. Тогда:

[math]T_{n}=F_{n-1}[/math].

[math]F_{n}=f_{n, n}[/math].

[math]f{n,k}=\sum\limits_{i=0}^{\lfloor \frac{n}{k} \rfloor} \binom{T_{k}+i-1}{i} s_{n-ik, k-1}[/math].

Количество таких деревьев с [math]n[/math] вершинами образуют последовательность A000081.

Помеченные деревья

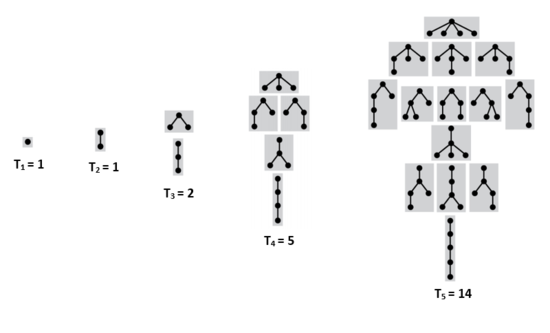
Утверждение:

Число помеченных бинарных деревьев с [math]n[/math] вершинами равно [math]T_n = n!\cdot C_n[/math].

[math]\triangleright[/math]

Как и в случае, с непомеченными бинарными деревьями, получаем производящую функцию для помеченных бинарных деревьев: [math]T(s) = \frac{1 - \sqrt{1 - 4s}}{2s}[/math]. Тогда: [math]T_n = n!\cdot [s\hat{}]\left(\dfrac{1 - \sqrt{1 - 4s}}{2s}\right) = n!\cdot C_n[/math]

[math]\triangleleft[/math]

Теорема (Кэли):

Число помеченных деревьев с [math]n[/math] вершинами равно [math]n^{n - 2}[/math].

Доказательство:

[math]\triangleright[/math]

Можно доказать формулу двумя способами. Первый способ. Так как между помеченными деревьями порядка [math]n[/math] и последовательностями длины [math]n - 2[/math] из чисел от [math]1[/math] до [math]n[/math] существует биекция (Код Прюфера), то количество помеченных деревьев совпадает с количеством последовательностей длины [math]n - 2[/math] из чисел от [math]1[/math] до [math]n = n^{n - 2}[/math]. Второй способ. С помощью матрицы Кирхгофа для полного графа на [math]n[/math] вершинах. Число помеченных деревьев порядка [math]n[/math], очевидно, равно числу остовов в полном графе [math]K_n[/math], которое есть [math]n^{n-2}[/math] по следствию теоремы Кирхгофа.

[math]\triangleleft[/math]

Утверждение:

Число помеченных корневых деревьев с [math]n[/math] вершинами есть [math]T_n = n^{n - 2}[/math].

[math]\triangleright[/math]

Данное утверждение является следствием теоремы Кэли. Обозначим через [math]T_n[/math] число корневых помеченных деревьев с [math]n[/math] вершинами, т.е. число помеченных деревьев, в которых одна из вершин выделена и названа корнем. Число корневых помеченных деревьев с [math]n[/math] вершинами в [math]n[/math] раз больше числа помеченных деревьев с [math]n[/math] вершинами: в качестве корня можно выбрать любую из [math]n[/math] различных вершин.

[math]\triangleleft[/math]

Дополнительно

Теорема (Скойнс):

Число 2-раскрашенных деревьев с [math]m[/math] вершинами одного цвета и [math]n[/math] вершинами другого равно [math]S_n = n^{m - 1} m^{n - 1}[/math].

См.также

• Лемма Бёрнсайда и Теорема Пойа
• Числа Каталана
• Генерация комбинаторных объектов в лексикографическом порядке